一 : 锐角三角形的三个内角是∠A、∠B、∠C，如果∠a=∠A＋∠B，∠b=∠B＋∠C，∠γ=∠C＋∠A，那

61阅读/ www.61k.net

锐角三角形的三个内角是∠A、∠B、∠C，如果∠a=∠A＋∠B，∠b=∠B＋∠C，∠γ=∠C＋∠A，那么∠a、∠b、∠γ这三个角中（）． （A）没有锐角（B）有1个锐角（C）有2个锐角（D）有3个锐角

题型：单选题难度：偏易来源：不详

A.

试题分析：由于锐角三角形中三个都是锐角，而α，β，γ分别是其外角，根据三角形外角的性质：三角形的任一外角等于和它不相邻的两个内角之和，可知α，β，γ这三个角都是钝角，没有锐角.

考点：

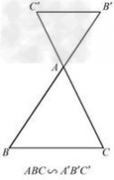
考点名称：相似多边形的性质

相似多边形：
如果两个边数相同的多边形的对应角相等，对应边成比例，这两个或多个多边形叫做相似多边形，相似多边形对应边的比叫做相似比。（或相似系数）
判定:
如果对应角相等,对应边成比例的多边形是相似多边形.
如果所有对应边成比例，那么这两个多边形相似

相似多边形的性质：
相似多边形的性质定理1：相似多边形周长比等于相似比。
相似多边形的性质定理2：相似多边形对应对角线的比等于相似比。
相似多边形的性质定理3：相似多边形中的对应三角形相似，其相似比等于相似多边形的相似比。
相似多边形的性质定理4：相似多边形面积的比等于相似比的平方。
相似多边形的性质定理5：若相似比为1，则全等。
相似多边形的性质定理6：相似三角形的对应线段（边、高、中线、角平分线）成比例。
相似多边形的性质定理7：相似三角形的对应角相等，对应边成比例。
相似多边形的性质定理主要根据它的定义：对应角相等，对应边成比例。考点名称：相似三角形的判定相似三角形：
对应角相等，对应边成比例的两个三角形叫做相似三角形。
互为相似形的三角形叫做相似三角形。

例如图中，若B'C'//BC，那么角B=角B'，角BAC=角B'A'C'，是对顶角，那么我们就说△ABC∽△AB'C'

相似三角形的判定：
1.基本判定定理
(1)平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似。
(2)如果一个三角形的两条边和另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似。(简叙为：两边对应成比例且夹角相等，两个三角形相似。)
(3)如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似。(简叙为：三边对应成比例，两个三角形相似。)
(4)如果两个三角形的两个角分别对应相等（或三个角分别对应相等），那么这两个三角形相似。
2.直角三角形判定定理
(1)直角三角形被斜边上的高分成两个直角三角形和原三角形相似。
(2)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似。
3.一定相似：
（1）.两个全等的三角形
（全等三角形是特殊的相似三角形，相似比为1：1）
（2）.两个等腰三角形
（两个等腰三角形，如果其中的任意一个顶角或底角相等，那么这两个等腰三角形相似。）
（3）.两个等边三角形
(两个等边三角形，三个内角都是60度，且边边相等，所以相似)　
（4）.直角三角形中由斜边的高形成的三个三角形。

相似三角形判定方法：
证两个相似三角形应该把表示对应顶点的字母写在对应的位置上。如果是文字语言的“△ABC与△DEF相似”，那么就说明这两个三角形的对应顶点可能没有写在对应的位置上，而如果是符号语言的“△ABC∽△DEF”，那么就说明这两个三角形的对应顶点写在了对应的位置上。
一、（预备定理）
平行于三角形一边的直线截其它两边所在的直线，截得的三角形与原三角形相似。（这是相似三角形判定的定理，是以下判定方法证明的基础。这个引理的证明方法需要平行线与线段成比例的证明）
二、如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
三、如果两个三角形的两组对应边成比例，并且相应的夹角相等,那么这两个三角形相似。
四、如果两个三角形的三组对应边成比例，那么这两个三角形相似
五（定义）
对应角相等，对应边成比例的两个三角形叫做相似三角形
六、两三角形三边对应垂直，则两三角形相似。
七、两个直角三角形中，斜边与直角边对应成比例，那么两三角形相似。
八、由角度比转化为线段比：h1/h2=Sabc

易失误
比值是一个具体的数字如：AB/EF=2
而比不是一个具体的数字如：AB/EF=2：1考点名称：相似三角形的性质

相似三角形性质定理：
(1)相似三角形的对应角相等。
(2)相似三角形的对应边成比例。
(3)相似三角形的对应高线的比，对应中线的比和对应角平分线的比都等于相似比。
(4)相似三角形的周长比等于相似比。
(5)相似三角形的面积比等于相似比的平方。
(6)相似三角形内切圆、外接圆直径比和周长比都和相似比相同，内切圆、外接圆面积比是相似比的平方
(7)若a/b =b/c，即b2=ac，b叫做a,c的比例中项
(8)c/d=a/b 等同于ad=bc.
(9)不必是在同一平面内的三角形里
①相似三角形对应角相等，对应边成比例.
②相似三角形对应高的比，对应中线的比和对应角平分线的比都等于相似比.
③相似三角形周长的比等于相似比

定理推论：
推论一：顶角或底角相等的两个等腰三角形相似。
推论二：腰和底对应成比例的两个等腰三角形相似。
推论三：有一个锐角相等的两个直角三角形相似。
推论四：直角三角形被斜边上的高分成的两个直角三角形和原三角形都相似。
推论五：如果一个三角形的两边和其中一边上的中线与另一个三角形的对应部分成比例，那么这两个三角形相似。
推论六：如果一个三角形的两边和第三边上的中线与另一个三角形的对应部分成比例，那么这两个三角形相似。

考点名称：相似三角形的应用相似三角形的应用：
应用相似三角形的判定、性质等知识去解决某些简单的实际问题（计算不能直接测量物体的长度和高度）。

二 : 如图，在△ABC中，∠C为直角，AB上的高CD及中线CE恰好把∠ACB三等分，若AB=20，求△ABC的两锐角及AD、DE、EB各为多少？

如图，在△ABC中，∠C为直角，AB上的高CD及中线CE恰好把∠ACB三等分，若AB=20，求△ABC的两锐角及AD、DE、EB各为多少？

如图，在△ABC中，∠C为直角，AB上的高CD及中线CE恰好把∠ACB三等分，若AB=20，求△ABC的两锐角及AD、DE、EB各为多少？的参考答案

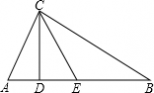
∵∠C为直角，CD、CE恰好把∠ACB三等分，

∴∠ACD=∠DCE=∠ECB=

1

3

×90°=30°，

∵CD是高，

∴∠A=90°-∠ACD=90°-30°=60°，

∵CE是中线，

∴CE=AE=EB=

1

2

AB=

1

2

×20=10，

∴∠B=∠ECB=30°，

∴AC=

1

2

AB=

1

2

×20=10，

AD=

1

2

AC=

1

2

×10=5，

DE=AE=AD=10-5=5．

综上所述：∠A=60°，∠B=30°，AD=5，DE=5，EB=10．

本文标题：如图ad为锐角三角形-锐角三角形的三个内角是∠A、∠B、∠C，如果∠a=∠A＋∠B，∠b=∠B＋∠C，∠γ=∠C＋∠A，那
本文地址： http://www.61k.com/1161607.html