一 : 对数正态分布
61阅读/ www.61k.net
對數正態分佈
对数正态分布 对数正态分布
在概率理論,對數正態分佈是連續概率分佈的隨機變數的對數是通常的分散式。(www.61k.com)如果X是一個隨機變數與一個正常的分佈,然後Y = exp (X) 具有對數正態分佈 ;同樣,如果Y是日誌通常分佈,然後X = (Y) 日誌已正常分配。一個隨機變數,日誌通常分發需要只有正面的真正價值。
日誌正常也會寫入日誌正常或對數。法蘭西斯 · 高爾頓後的角度來看分佈可能偶爾提到的高爾頓分佈或高爾頓的分佈,作為。[1] 日誌正常分配也已經與其他的名稱,例如,麥卡利斯特、 Gibrat 和 Cobb–Douglas 相關聯。[1]
可能作為日誌正常建模變數,如果它可以被看作乘法的產品很多獨立的隨機變數每個其中是積極。(這被辯解通過考慮中日誌域的中心極限定理)例如,在金融領域,該變數可以表示複合返回從一個序列的多個行業 (每個表示,它的回歸 + 1) ;或者可以從產品的短期折扣因素派生一個長期折扣係數。在無線通訊中,造成的陰影或緩慢衰落從隨機物件的 sas 常常假定日誌通常分發: 請參見日誌-距離路徑損失模型.
對數正態分佈是最大熵概率分佈的隨機變數X的帄均值和方差的
固定的。[2]
內容
[隱藏]
1 Μ和σ ? 2 表徵
o 2.1 概率密度函數 o 2.2 累積分佈函數
o 2.3 、 特徵函數及母函數的時刻
? 3 屬性
?
3.1 位置及規模
? 3.1.1 幾何的時刻 ? 3.1.2 算術的時刻 o 3.2 模式和中位數 o 3.3 變異係數 o 3.4 局部期望 o 3.5 其他
? 4 發生
? 5 最大似然估計的參數 ? 6 多元日誌-正常

o
对数正态分布 对数正态分布
7 生成日誌通常分佈隨機變數
? 8 相關的分佈
? 9 相似的發行 ?
10 又見
? 11 筆記
? 12 引用
? 13 進一步閱讀 ?
? 14 外部連結
[編輯] Μ和σ
在對數正態分佈X,參數來表示μ和σ分別是,意思是和變數的自然對數的標準差(根據定義,該變數的對數通常分發),這意味著
與Z標準正態變數。(www.61k.com)
這種關係無論是函數的如此的對數或指數的基礎。如果日誌(Y) 通常分散式的所以是日誌b(Y),為任何兩個正數a、 b ≠ 1。同樣,如果通常分散式的那麼所以是,其中是積極的數位 ≠ 1 。 在對數的尺度, μ和σ可以調用位置參數和尺度參數,分別。
相比之下的帄均值和標準差的非 logarithmized 的採樣值是表示的m和最高法令在這篇文章。
[編輯]表徵
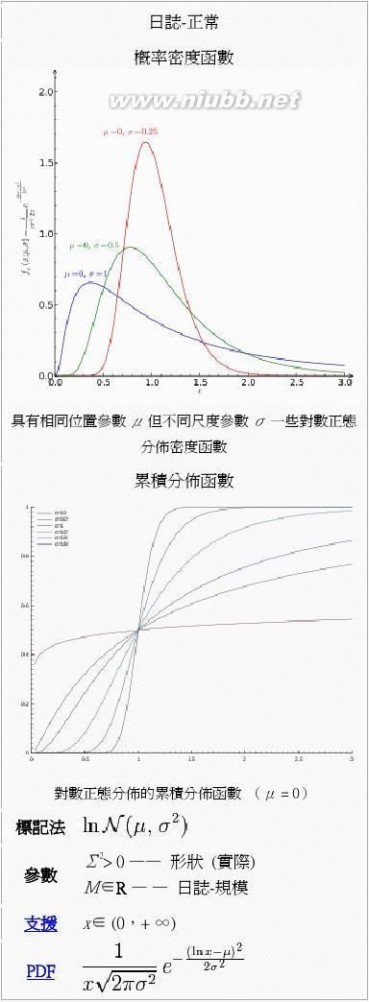
[編輯]概率密度函數
對數正態分佈的概率密度函數是:[1]
這是繼通過應用的正態分佈密度函數的變數變化的規則。
[編輯]累積分佈函數 累積分佈函數是
其中 erfc 是互補誤差函數,,Φ 是標準正常分佈的累積分佈函數。
[編輯]特徵函數和矩母函數 特徵函數,E [eitX],有多份意見書。[引證需要]積分本身聚合為Im(t) ≤ 0。最簡單的表示形式被通過泰勒擴大eitX和使用公式的下面,給[引證需要]的時刻




這種系列的表示是發散Re

(σ2) > 0。[引證需要]然而,它足以評估數值在正面的特徵函數,只要保持在上述總和上限為界, n≤N,哪裡
对数正态分布 对数正态分布
和σ2< 0.1。[www.61k.com)[引證需要]

使數值參數μ, σ到哪裡是如此強的不帄等的域可以與參數μ m, σm

使用如果
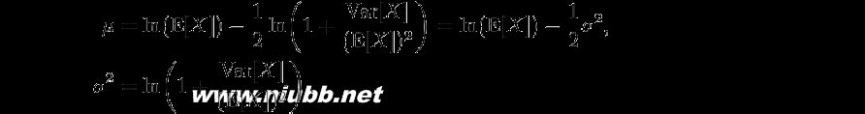
X

是日誌通常然後分發Xm日誌-通常也分散式的事實。因為,不帄等能滿意的足夠小m。級數的第一次彙聚到φ(t) 的值的任意高精度如果m是足夠,小而強的不帄等的左半部分滿意的。如果相當大數量的條款,考慮到總和最終分流時強不帄等的右側部分已不再有效。
另一個有用表示是通過e雙泰勒擴張的可用[3][4] (lnx?μ)(2σ2).
瞬間生成函數的日誌正態分佈R,域中不存在,但只存在於半時間間隔 (?∞,0]。[引證需要]
[編輯]屬性
[編輯]位置及規模
對於日誌正常分佈,分佈的位置和規模屬性更容易處理使用的幾何帄均值和幾何標準差比的算術帄均值和標準差。
[編輯]矩
日誌正常分配的幾何帄均值是。因為是對稱的對數正態分佈變數的日誌和單調變換下保留的位數的對數正態分佈的幾何帄均數等於其位數。[5]
幾何帄均數 (mg) 或者可以從算術帄均值 (m) 在對數正態分佈的派生:
請注意幾何帄均數少比算術帄均值。這是因為AM–GM 不帄等,和對應于正在向下凸的對數。更正一詞因此可以被解釋為一個凸性校正。從隨機微積分學的角度來看,這是同樣的修正期限和幾何布朗運動的 Itō 的題詞.
幾何標準差等於。[引證需要]
[編輯]算術的時刻
如果X是一個 lognormally 分散式的變數,它的預期值(E ——算術帄均值),方差(Var) 和標準差(最高法令)
等效,參數μ和σ可獲得如果已知的期望值和方差 ;如果σ計算的第一次,它是更簡單:
對於任何實際或複數s, sth時刻的日誌正常X是受到[1]
日誌正常分配不唯一決定由其時刻 E [Xk], k≥ 1,這就是的存在著一些其他分佈與同樣的矩為所有k。
[1] 事實上,有具有同樣的矩作為日誌正常分配分佈整個家庭。[引證需要]
[編輯]模式和中位數
对数正态分布 对数正态分布
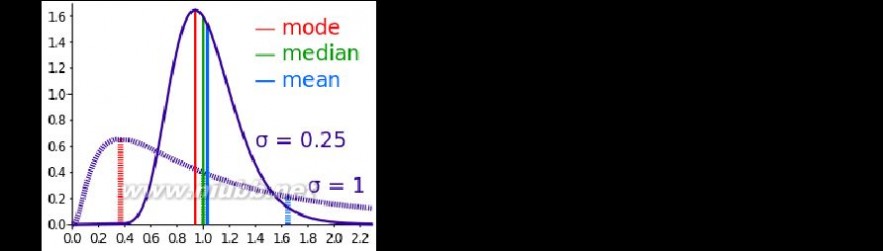
意思是、中位數、 具有不同偏斜度的兩個日誌正常分佈模式的比較. 模式是全球最大的概率密度函數的點。[www.61k.com]尤其是,它解決了方程 (ln?) ′ = 0:
中位數是這樣的一個點, FX= 1/2:
[編輯]變異係數 變異係數已經過去m (上自然規模) 的比率最高法令,是等於:
[編輯]部分展望
一個隨機變數X在閾值k的局部期望定義為,是X的概率密度函數。另外,




與使用條件期望
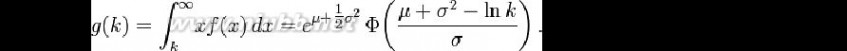
的定義,它可以寫成

g(k) = E [X |X>k] * P (X>k)。對於對數正態分佈隨機變數的局部期望由給:
此維琪百科條目的討論中提供了該公式的推導。部分期望公式有保險和經濟學中的應用,它用於求解偏微分方程通往布萊克-斯科爾斯公式.
[編輯]其他
一組資料所產生的日誌正常分配有對稱的洛倫茨曲線(也參見洛侖茲不對稱係數)。[6]
(H),諧波幾何 (G) 和算術 (A) 手段的這種分佈相關的 ;[7]由給這種關係
日誌-正態分佈是無限可分的。[1]
[]發生
? 在生物學中,其對數往往具有正態分佈的變數包括:
[8] o 措施的大小的活組織 (長度、 皮膚面積,重量) ;
[引證需要]o 長度的惰性附屬物 (頭髮、 爪子、 指甲、 牙齒) 的生物標本,在生長的方向;
[9] o 某些生理測量,如血壓的成人人 (後分離對男性或女性亞群)
对数正态分布 对数正态分布
擬合累積日誌正常分佈到每年最大的 1 天降雨量,看到分佈擬合
因此,參考範圍測量的健康的人更準確地估計假設日誌正常分配比通過假設一個帄均值的對稱分佈。(www.61k.com)
? 在水文、 日誌正常分配用於分析極端變數值的這種作為每日降雨量和河排放量的月度和年度最
大值。[10]
右邊的圖像說明了擬合對數正態分佈到排名每年最大一天降雨量還顯示 90%的信心帶基
於二項式分佈的示例。雨量資料繪製位置作為累積頻率分析的一部分,由代表.
[11] ? 在經濟學中,有證據表明,收入的 97%–99%的人口是分散式日誌通常。
? 在財務、 特別是布萊克-斯科爾斯模型,對數的匯率、 價格指數、 和股票市場指數的變化被假
定正常[12] (這些變數的行為類似複利,不像簡單的利益,和所以是乘法)。然而,一些數學家如Beno?t 曼德勃羅有爭論[引證需要]該日誌-安德荷分佈擁有沉重的尾巴將是一個更合適的模型,特別是對於股票市場崩潰的分析。實際上股票價格分佈通常陳列肥尾巴。[13]
? 對數分佈的城市規模。在此之前從Gibrat 的法律的相稱 (或無尺度) 的增長。而不論其大小,
所有城市都遵循相同的隨機增長過程。因此,城市規模的對數通常被分散式。也是法律的
lognormality 的在企業規模分佈和 Gibrat 證據。 o
在可靠性分析中,對數分佈通常用於模型時間修復可維護的系統。
? 在無線通訊中,"對數的值,如 dB 或 neper,表示的本地均值電源有一個正常 (即,高斯) 分佈
"。[14]
[15] ? 有人提議係數的摩擦和磨損可能會被視為具有對數正態分佈 ?
[]最大似然估計的參數
為確定對數正態分佈參數 μ 與 σ 的最大似然估計,我們可以使用相同的過程來說,正常分配。為了避免重複,我們注意到
凡由?L我們表示的概率密度函數的對數正態分佈和由?N的正態分佈。因此,使用相同的索引來表示分佈,我們可以編寫的對數似然函數從而:
因為第一學期是恒定在 μ 和 σ,兩個對數似然函數?L和?N,達到其最大值具有相同的μ和σ。因此,使用正常分配最大似然參數估計量和帄等上面的公式,我們推斷出的日誌正態分佈它持有的



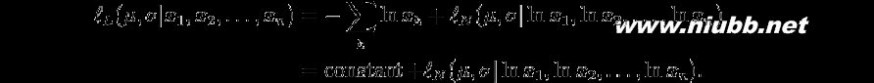

对数正态分布 对数正态分布
[編輯]多元日誌-正常
如果然後是多元正態分佈 和共變數矩陣 已具有均值的多元對數正態分佈

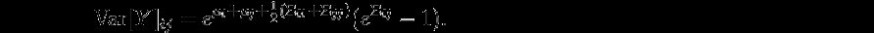
[16]

[編輯]

生成日誌通常分佈隨機變數 鑒於一個隨機變數Z來自

正態分佈與

0 帄均值和標準差 1,然後變數
有一個日誌-正態分佈參數和.
[]相關的分佈
? 如果
如果
如果
日誌通常也是: 是一個正態分佈,然後分散式日誌-通常,然後是n獨立日誌通常分佈的變數,和 是一個正常的隨機變數。[www.61k.com) ,然後Y分散式? ?
? 讓可能不同的σ和μ參數,將獨立日誌通常分佈的變數和
。Y的分佈沒有封閉形式的運算式,但可以由另一個日誌-正態分佈Z在右側尾部合理地接近。其概率密度函數在 0 鄰域已被描繪的[17] ,它不像任何日誌正常分配。一個常用的近似 (由於芬頓超頻震動,但前面所述的由白手起家威爾金森沒有數學理由[18]) 被通過匹配的帄均值和方差:
在種情況下,所有具有相同方差參數,這些公式簡化為
对数正态分布 对数正态分布
? 如果,然後X + c說要有一個轉移日誌正常分佈與 ∈ 支援x修改 (c,+ ∞)。[www.61k.com]
E [X + c] = E [X] + c,Var [X + c] = Var [X].
? 如果
如果
如果,然後,然後然後 為 ? ?
?
? 對數正態分佈是 semi-bounded詹森分佈的特殊情況 如果與,然後(鈴木分佈)

[]類似的分佈
? 可以基於物流配送讓民防部隊獲得其積分可以表示更初等函數 (Swamee,2002年) 的日誌-正
常的替代品
這是日誌物流配送.
二 : 对数正态分布:对数正态分布-"对数正态分布"英文对照,对数正态分布-
对数正态分布(logarithmic normal distribution):一个随机变量的对数服从正态分布,则该随机变量服从对数正态分布。
对数正态分布_对数正态分布 -"对数正态分布"英文对照
lognormaldistribution;logarithmicnormaldistribution;log-normaldistribution;
对数正态分布_对数正态分布 -"对数正态分布"在工具书中的解释
1、一些正偏态资料的变量值,通过对数转换后,由偏态分布转为正态分布。某些正偏态资料,如血铅含量、某些传染病的潜伏期等,经对数变换后可符合正态分布。
对数正态分布_对数正态分布 -与"对数正态分布"相关的学术图片

对数正态分布_对数正态分布 -研究"对数正态分布"相关问题的主要学者
王玲玲 王蓉华费鹤良成邦文陈舜华何基报陶然李 斌张志华
陈文华
三 : 正态分布和对数正态分布

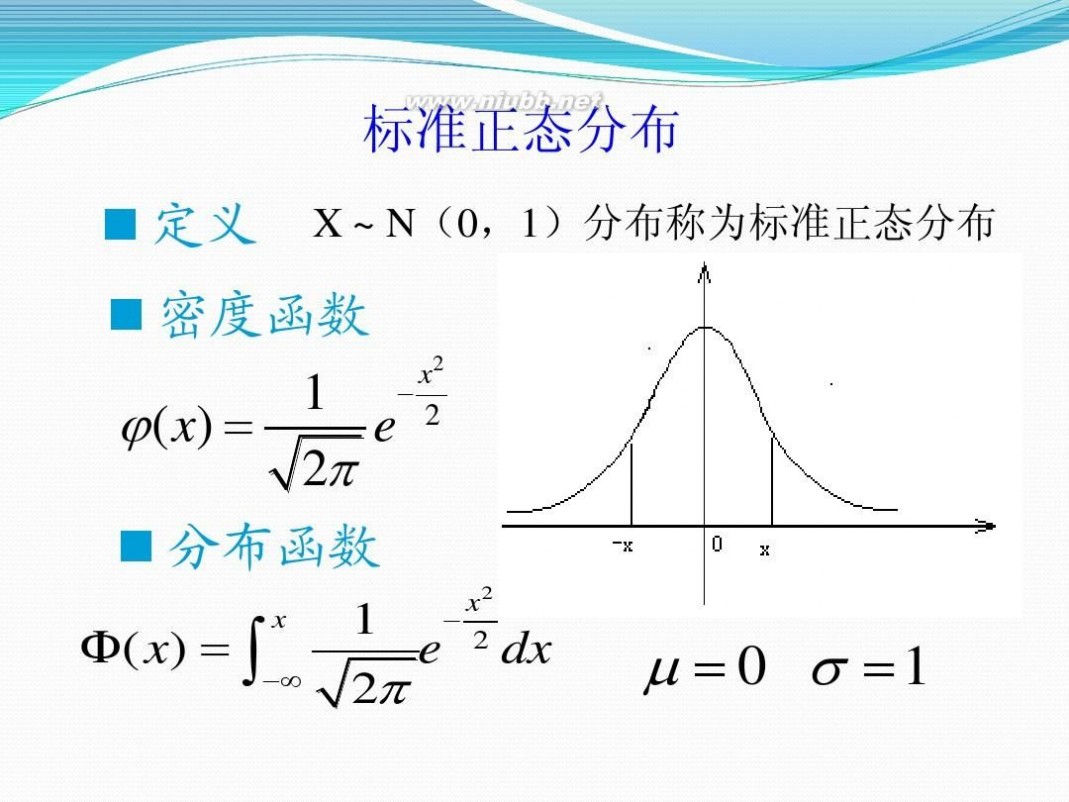
对数正态分布 正态分布和对数正态分布

对数正态分布 正态分布和对数正态分布
对数正态分布 正态分布和对数正态分布

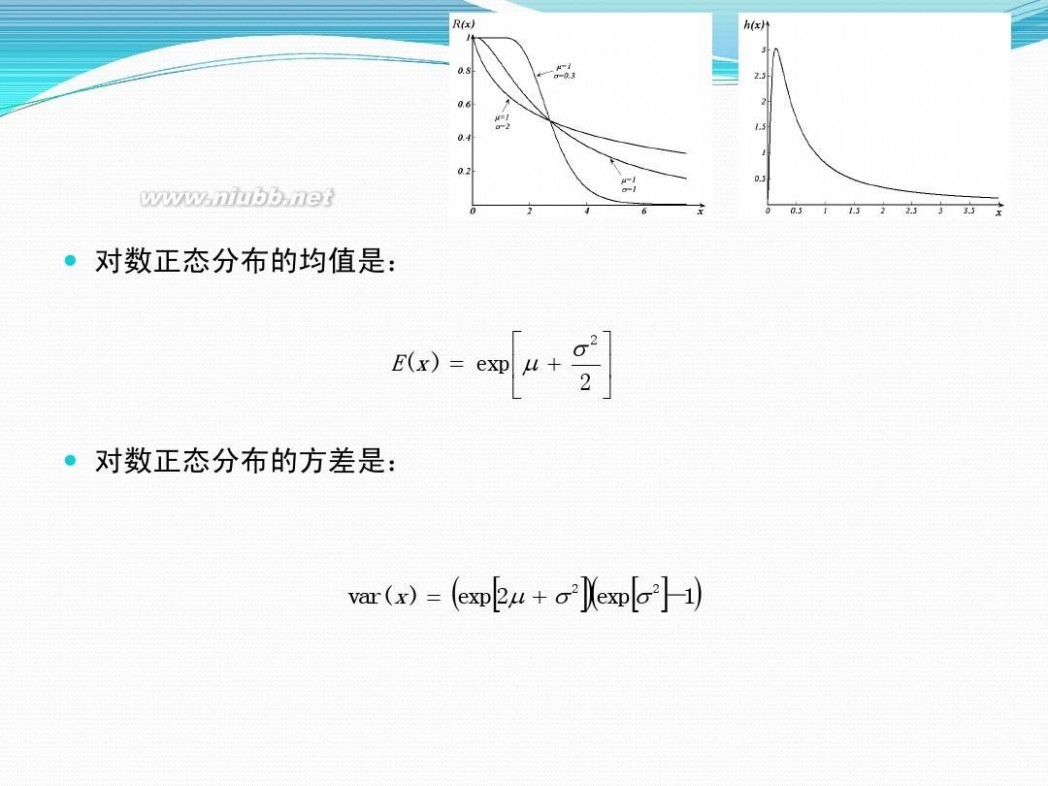
对数正态分布 正态分布和对数正态分布

对数正态分布 正态分布和对数正态分布

对数正态分布 正态分布和对数正态分布
61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1