一 : 多目标路径规划问题的算法综述_潘斌斌

第29卷第5期Vol.29NO．5重庆工商大学学报（自然科学版）JChongqingTechnolBusinessUniv.（NatSciEd）2012年5月May2012文章编号：1672－058X（2012）05－0078－07

多目标路径规划问题的算法综述

潘斌斌

（重庆交通大学管理学院，重庆400074）

摘要：单目标路径优化模型难以更好的模拟实际生活中复杂多变的状况，相比而言多目标路径优化更贴近于现实，对实际问题更具有指导意义，也是近年来计算机科学和物流科学研究的一个热点问题，产生了众多的研究成果；为全面总结多目标路径优化算法的研究现状，综述了国内外多目标路径优化算法在不同背景下的应用及取得的进展，并按算法的构造方法进行了相应的分类；最后进行了总结分析了存在的问题，并指明其进一步的研究方向。

关键词：多目标；路径优化；NP难题；精确算法；启发式算法

中图分类号：TP374文献标志码：A

1引言

路径规划问题指涉及在一个网络中，找出一条满足一系列约束的路线，且使一个目标或多个目标最优

包括著名的旅行商问题（TravelingSaleman化的一类问题。路径规划问题是一类被广泛研究的问题，

Problem，TSP）、VRP）、车辆路径规划问题（VehicleRoutingProblem，应急疏散路线设计、救济品及危险品运输路线设计、物流配送优化等。路径选择时，通常考虑单个目标（如成本最小化）进行优化，而实际生活中这类问题是一个复杂的多目标问题-文章窝-，确定性的单目标的路径优化已不能满足实际需求，能提供的意义是有限的，多目标路线规划模型能更好的贴近现实，具有重要的科研价值和实际意义。在物流业大力发展、城市交通规划的发展、绿色环保的倡导下及单目标路径优化的片面性，多目标的路径优化研究逐渐成为研究的热点。在此对多目标路径规划问题的算法进行了综述，并展望了研究前景。

2各种算法在多目标路线规划中的应用

一般情况下，多目标优化问题的各个子目标之间是矛盾的，一个子目标的改善有可能会引起另一个或另几个子目标的性能降低，即要同时使多个子目标一起达到最优值是不可能的，而只能在它们中间进行协调和折中处理，使各个子目标都尽可能地达到最优化。多目标优化问题不存在唯一的全局最优解，过多的非劣解是无法直接应用的，所以在求解时要寻找一个最终解。求最终解主要有三类方法［1］：（1）生成法，即

构成非劣解的一个子集，然后按照决策者的意图找出最终解；（2）交互法，不先求出很先求出大量的非劣解，

多的非劣解，而是通过分析者与决策者对话的方式逐步求出最终解；（3）权重法，其主旨是将所有的目标函

收稿日期：2011－08－21；修回日期：2011－09－27．

），作者简介：潘斌斌（1988-男，浙江省温岭市，硕士，从事供应链与企业物流管理研究．

第5期潘斌斌：多目标路径规划问题的算法综述79数，依据其重要性乘以一个权值，然后求和，转化为单目标问题进行求解。而这些主要是通过算法来实现的。

大量文献分析表明：多目标路线规划问题的研究方法主要分为两大类，即精确算法和启发式算法。由于精确算法（如动态规划、整数规划等数学规划方法）难以解决大规模的复杂多目标路线规划问题，启发式优化方法在多目标路线规划问题研究中应用的较多。

2．1整数规划法

整数规划（integerprogramming）主要应用于规模有限的多目标路线规划问题上。其基本思路是首先分

Lingo等数学软件进行求解，析问题的特性，再构造出对应的整数规划模型，最后利用Matlab、可以直接给出

［2］路线的分配情况，但只有一个确定解。AlexanderStepanov等人在疏散路线的设计中利用整数规划进行求

［3］提出了多目标整数线性规划来进行集装箱供应链解。HUZhiHua针对集装箱多式联运紧急救济的网络，

的路径选择，将多个目标进行整合成单个目标，最后通过传统的软件包进行求实现时间及成本最小化。

2．2动态规划算法

动态规划算法（Dynamicprogramming）适用于解决那些可分解为重复子问题（overlappingsubproblems）并具有最优子结构（optimalsubstructure）的问题，通常比其他普通算法节约更多时间。动态规划算法通常采用以下两种方式：（1）自顶向下，将问题划分为若干子问题，求解这些子问题并保存结果以免重复计

该方法将递归和缓存结合在一起。（2）自下而上，先行求解所有可能用到的子问题，然后用其构造更算，

大问题的解。

KonstantinosN等［4］针对多目标路线规划问题，将问题分解为一系列路线子问题，通过动态规划算法进

［5］行求解。LineBlanderReinhardt等人针对条件和目标不可累加的多目标最短路问题，给出了一个通用的

最后用动态规划算法进行求解。公式来处理一系列不可累加的条件，

2．3启发式算法

多目标优化问题往往通过加权等方式转化为单目标问题，然后用数学规划的方法来求解，每次只能得

由于多目标优化问题的目标函数和约束函数可能是非线性或不可微到一种权值情况下的最优解。同时，

的，及随着问题规模的增大，问题的复杂度也相应增加，计算的时间也将呈指数级增加，影响了最优算法的效率。一般最优算法应用于数据规模较少的多目标路线规划问题中。对于涉及大规模的多目标路线规划问题，启发式算法（heuristicalgorithms）提供了一种效率较高的求解途径。

Jean-FrancoisBérubé等人［6］提出了将多个目标转化为解决一个单目标的子针对多目标的旅行商问题，

使所有目标转化为约束，并用基于可从前面子问题收集信息的启发式算法加快处理速度，解决了收集问题，

Juliane到奖金最大化且旅行费用最低的旅行商问题。针对双目标的带时间窗的车辆路径规划问题，

［8，9］Müller［7］提出了一种启发式算法，实现总的运输车辆数和运输距离最小。首先，利用Solomon提出的途程

再将途程改善启发式算法（RouteImprovement建构启发式算法（routeconstructionheuristic）得到初始解，

Heuristics）应用到当前解中减少车辆的数目和距离。以及在文献［10］11］和文献［中研究者针对多目标路径规划问题也提出了启发式算法进行求解。

2．4元启发式算法

heuristicalgorithms）是一种通用型的启发式算法，元启发式算法（meta-是对启发式算法的改进，优化机

理不过分依赖待解问题的结构，结合了随机方法和搜索算法。主要包括遗传算法（geneticalgorithm）、模拟退火算法（simulationannealingalgorithm）、禁忌搜索算法（tabusearchalgorithm）、粒子群算法（particleswarmoptimization）、蚁群算法（antcolonyalgorithm）、贪婪随机自适应搜索算法（GreedyRandomizedAdaptiveSear chProcedure）等。这些方法被逐渐引入到多目标路线规划问题研究中，并取得了一定的研究进展。

80

2．4．1遗传算法重庆工商大学学报（自然科学版）第29卷

遗传算法（geneticalgorithm）是是一种借鉴生物界自然选择和进化机制发展起来的高度并行、随机、自适应搜索的仿真优化算法，它使用种群代表一组解，通过对当前种群进行选择、交叉和变异等一系列遗传操作，产生新一代种群，周而复始，直到满足终止条件得到包含近似最优解为止。

在多目标路线规划问题研究中，遗传算法往往通过以下方法对模型进行求解：与传统优化技术结合；将遗传算法同其他启发式方法相结合构造混合遗传算法来求解；模糊理论、权重法与遗传算法的结合。

P．Lacomme等人［12］受非支配排序遗传算法（Non-dominatedsorted在车辆路径规划问题（VRP）中，

［13］geneticalgorithm）的启发，构建了启发式算法来求解多目标的车辆路径规划问题。K．C．Tan等人提出了

该方法具有专用的遗传算子，可变长度的表示法和局部搜索启发式法来混合的多目标进化算法（HMOEA），

同时使路径距离和卡车数最小化的多目标问题。许国银等人求解决路线日程安排，［14］综合考虑战时配送

VRP（vehicleroutingproblem）的多个评价目标，基于重要性的多目标分层优化思想，建立了完全分层优化模

［15］将进化算法和传统优化技术相结合，构造了模型的两层求解算法。H．C．W．Lau等人考虑了多个仓型，

库、多个顾客和多种物品，为实现总的运输距离，总的运输时间最优，提出模 糊理论指导的非支配排序遗传

NSGA2）的多目标进化算法。WANGChungHo等人［16］为使总的配送路线最小化及通过满足时间算法2（FL-

窗的要求使顾客对服务的满意度最大化，提出了基于贪婪算法、遗传算法的混合算法来求解多目标模型中

17-19］中，其他研究者也提出了基于遗传算法的元启发式算法。在旅行商问题中，的变量。以及在文献［

FundaSamanlioglu等人［20］提出了memeticrandom-key遗传算法。

在其他多目标路线优化问题中，井祥鹤等人［21］提出了一种求解多式联运运输方式选择多目标优化问题

［22］的混合遗传算法，给出了染色体编码、遗传算子设计、染色体有效性判断和修正的方法。林勇等人在解决

GA）中融入了NSGA-多目标运输优化问题的基于生成树的遗传算法（st-Ⅱ算法，提出了一种新的生成树遗

GA），采用精英保留和擂台法来进行遗传选择，算例结果表明新算法提高了收敛速度，防止了传算法（NSST-

23］早熟收敛，较好的保持了种群多样性和算法的稳定性。以及在文献［中，其他研究者也提出了基于遗传

算法的元启发式算法。

2．4．2蚁群算法

［24］蚁群算法（AntColonyOptimization）是一种新型的模拟进化算法，由M．Dorigo等人首先提出。与其他

元启发式算法不同，它采用分布构建解的流程，每只蚂蚁选择下一步时，需要参考整个种群的累积经验和启发式信息。ACO算法求解路径优化问题的流程［25］如下：（1）蚂蚁群体初始化；（2）循环以下过程直到满足

信息素挥发，可选的全局操作；（3）输出最优路径。终止条件：所有蚂蚁选路并释放信息素，

YUANYuan等人［26］针对危机物流管理问题，提出了一个多目标路径选择模型用来使沿通道转移的时

［27］间最小化和使路径复杂度最小化，并用蚁群算法进行了求解。KeivanGhoseiri等人针对多目标最短路问

题（MOSP），提出了一种基于多目标优化的蚁群算法（ACO）来解决双目标最短路问题。FANGZhiXiang等人［28］针对疏散路线的网络规划，提出了多目标优化来解决基于多层决策网络的疏散路线规划问题，最后利

粒子群算法用蚁群优化算法进行求解。2．4．3

粒子群算法（ParticleSwarmOptimization）和遗传算法相似，也是从随机解出发，通过迭代寻找最优解，但

不涉及交叉、变异操作，而是通过追随当前最优值来找到全局最优解。粒子群算在规则上比遗传算法简单，

［29］法应用于多目标路径规划的研究中的文献相对较少。XUJiuPing等人针对模糊随机环境下的带软时间

窗的车辆路径问题（VRPSTW）。考虑如下两个目标：总的运输费用最小化；使所有顾客的平均服务水平最大

PSO-EP）用来求解该问题。化。提出了可变粒子的全局-局部-邻近粒子群优化算法（GLN-

第5期潘斌斌：多目标路径规划问题的算法综述81

2．4．5贪婪随机自适应搜索算法

［30］GRASP）是一种新的元启发式贪婪随机自适应搜索算法（GreedyRandomizedAdaptiveSearchProcedure，算法，主要包含贪婪函数、自适应过程、随机组成和局域搜索4个方面，由FEO等人提出。GRASP是一个

每次迭代过程包含两个阶段：构造阶段和局域搜索阶段。得益于GRASP在初始构造启发式随机迭代过程，

在计算速度上会比一般的启发式算法如遗传算法等快，随着问题规模的加大，阶段采取了适当启发式策略，

速度上的优势会比较明显。

RafaelMartí将GRASP应用与多目标路径优化研究方面的文献较少。在为危险物品选择交通路线时，

等人［31］介绍了一种双目标优化模型，提出了用改进的GRASP进行求解。RafaelMartí等人做的主要改进是

多目标遗传局部搜索算法将随机分解方法RDE融入到构造阶段而提出了改进的GRASP。2．4．6

多目标遗传局部搜索算法（Memetic算法）是求解多目标优化问题最有效地方法之一，融合了局部搜索和进化计算，具有较高的全局搜索能力。这种算法加强了搜索算法的目的性，加快了收敛到局部最优解的

［32］针对双目标的旅行商问题提出了融入Pareto局部搜索算法的Pareto速度。AndrzejJaszkiewicz等人

memetic算法，经实验证明该算法有效地改进了计算结果。

2．4．7禁忌搜索算法

［33］禁忌搜索算法（TabuSearchAlgorithm）是一种亚启发式搜索算法，从一个初始可行解出发，选择一系列的特定搜索方向（移动）作为试探，选择实现让特定的目标函数值变化最多的移动。王君等人

提出了多目标禁忌搜索算法。模糊预约时间的多目标车辆路径问题，

2．5其他方法

（1）Zimmermann方法（模糊多目标线性规划）和广义简约梯度算法。考虑不精确的单位费用和路线方

A．Ojha等人［34］依据Zimmermann方法和模糊等价面的运输时间（广义模糊数）的多目标多模式运输问题，

性措施将多目标优化减少到单目标优化问题，然后利用广义简约梯度算法

找到最优的解决方案。

（2）反向演算法。针对基于时间的双标准最短路问题（TdBiSP），HorstW．Hamacher等人［36］提出了反向演算法进行求解。

（3）整合参数化方法和模糊聚类方法。模糊聚类方法是以隶属度作为聚类的出发点，以模糊等价矩阵

［37］提出了整合参作为启发规则的算法。PhysicsLettersA等人针对多目标动态优化的最优化路径规划问题，［35］在针对带（GRG）用来从一大堆数据中

数化方法和模糊聚类方法进行求解。

（4）Martin算法。TristramGrbener等人［38］针对基于时间的多目标最优路径提出Martin算法进行求解。

3结束语

虽然多目标路径规划问题的研究已取得了一定的研究成果，但由于在这一领域的大部分问题都没有唯一的全局最优解且具有NP难题特性，而各种算法又都有其自身的缺陷，至今尚未有非常高效的解决方法和理论。通过对路径规划领域的多目标优化算法的综述，归纳了多目标路径优化算法的几个未来研究方向：

（1）文献中研究的大部分多目标路径优化问题基于静态环境下的居多，难于应用与现实中复杂多变的环境。相对静态环境下的多目标路径优化问题，动态环境下的多目标路径优化问题更贴近实际应用。如时变环境下的多目标路径优化将是未来研究的重点。

82重庆工商大学学报（自然科学版）第29卷

（2）与精确算法相比，元启发式算法尽管相对简单、灵活，计算效率高，但不一定能保证所得解的可行性和全局最优性，甚至在多数情况下，无法分析所得解同最优解的近似程度。因此，为了克服各种元启发式算法的缺点和发挥其各自的优势，将两种或两种以上启发式算法结合起来形成更加高效的混合智能启发算法，将是多目标路径优化算法研究的重要方向之一。

（3）多目标优化问题难以找到一个最优解，大多是在各个目标间权衡、协调寻求一个折中解。而将模糊

能够较好的考虑不同性质的、相互矛盾的多个目标的满意程度，使各个目标理论引入到多目标规划问题中，

在约束条件下都最大程度地实现。为解决多目标优化问题提供了新的途径，如模糊理论指导下的遗传算法等将成为未来多目标路径优化算法的研究的一个热点。

参考文献：

［1］肖晓伟，J］．计算机应用研究，2011，28（3）：805-808肖迪，林锦国，肖玉峰．多目标优化问题的研究概述［

［2］ALEXANDERS，JAMESM．Multi-objectiveevacuationroutingintransportationnetworks［J］．EuropeanJournalofOperational

Research，2009，198（2）：435-446

［3］HUZHH．Acontainermultimodaltransportationschedulingapproachbasedonimmuneaffinitymodelforemergencyrelief［J］．

2011，38（3）：2632-2639ExpertSystemswithApplications，

［4］KONSTANTINOSN，ANDROUTSOPOULOSK．Solvingthemulti-criteriatime-dependentroutingandschedulingproblemina

multimodalfixedschedulednetwork［J］．EuropeanJournalofOperationalResearch，2009，1（1）：18-28

［5］LINEBR，DAVIDP．Multi-objectiveandmulti-constrainednon-additiveshortestpathproblems［J］．Computers＆Operations

2011，38（3）：605-616Research，

［6］JEANn-FRANOISRUB，MICHELG，JEAN-YVESP．Anexactε-constraintmethodforbi-objectivecombinatorialoptimization

J］．EuropeanJournalofOperationalResearch，2009，194problems：ApplicationtotheTravelingSalesmanProblemwithProfits［

（1）：39-50

［7］JULIANEM．ApproximativesolutionstothebicriterionVehicleRoutingProblemwithTimeWindows［J］．EuropeanJournalof

OperationalResearch，2010，202（1）：223-231

［8］MARIUSM．Algorithmsforthevehicleroutingandschedulingproblemswithtimewindowconstraints［J］．OperationsResearch，

1987，35（2），254-264

［9］MARIUSM，JACQUESD．Timewindowconstrainedroutingandschedulingproblems［J］．TransportationScience，1988，22（1），

1-13

［10］CHANGT．Bestroutesselectionininternationalintermodalnetworks［J］．Computers＆OperationsResearch，2008，35（9）：

2877-2891

［11］CARAMIAM，GUERRIEROF．Aheuristicapproachtolong-haulfreighttransportationwithmultipleobjectivefunctions［J］．

EuropeanJournalofOperationalResearch，2009，37（3）：600-614

［12］LACOMMEP，PRINSC，SEVAUXM．Ageneticalgorithmforabi-objectivecapacitatedarcroutingproblem［J］．Computers＆

OperationsResearch，2008，35（9）：3473-3493

［13］TANKC，CHEWYH，LEELH．Ahybridmulti-objectiveevolutionaryalgorithmforsolvingtruckandtrailervehiclerouting

problems［J］．EuropeanJournalofOperationalResearch，2006，172（3）：855-885

［14］许国银，J］．解放军理工大学学报：自然科学版，2007，熊孝和，林涛．基于GASA算法的成品燃油战时公路配送路径优化［

8（2）：180-185

［15］LAUHCW，CHANTM，TSUIWT，etal．Afuzzyguidedmulti-objectiveevolutionaryalgorithmmodelforsolvingtransportation

problem［J］．ExpertSystemswithApplications，2009，36（4）：8255-8268

［16］WANGC，LIC．Optimizationofanestablishedmult i-objectivedeliveringproblembyanimprovedhybridalgorithm［J］．Expert

SystemswithApplications，2011，38（4）：4361-4367

第5期潘斌斌：多目标路径规划问题的算法综述83［17］NICOLASJ，FRDRICS，El-GHAZALIT．Anevolutionaryalgorithmfortheveh icleroutingproblemwithroutebalancing［J］．

Computers＆OperationsResearch，2009，195（3）：761-769

［18］KEIVANG，SEYEDF．Multi-objectivevehicleroutingproblemwithtimewindowsusinggoalprogrammingandgeneticalgorithm

［J］．AppliedSoftComputing，2010，10（4）：1096-1107

［19］徐慧英，J］．计算机工程与科学，2010，32赵建民，张泳，朱信忠．改进NSGAII算法在车辆路径多目标优化问题中的应用［

（10）：117-121

［20］FUNDAS，WILLIAMG，FERRELLJ，etal．Amemeticrandom-keygeneticalgorithmforasymmetricmulti-objectivetraveling

J］．Computers＆IndustrialEngineering，2008，55（2）：439-449salesmanproblem［

［21］井祥鹤，J］．计算机工程与应用，2008，44（6）：210-212魏冬峰，周献中．运输方式选择多目标优化问题的混合遗传算法［

［22］林勇，GA遗传算法在多目标运输问题中的应用［J］．西南民族大学学报：自然科学版，2009，35张洪伟，沈哲宇．改进ST-

（6）：1161-1164

［23］高庆春，J］．信息技术，2010，5（28）：38-38韩应征，张立毅．军事应急物流中多目标路径优化的研究［

［24］DORIGOM，MANIEZZOV，COLORNIA．Theantsystem：Optimizationbyacolonyofcooperatingagents［J］．IEEE

Man，andCyberneticsPartB，1996，26（1）：29-41TransactionsonSystems，

［25］DORIGOM，MANIEZZOV，COLORNIA．Antcolonyoptimizationanewmeta-heuristic［J］．EvolutionaryComputation．1999：

1470-1477

［26］YUANY，WANGD．Pathselectionmodelandalgorithmforemergencylogisticsmanagement［J］．Computers＆Industrial

2009，56（3）：1081-1094Engineering，

［27］KEIVANG，BEHNAMN．Anantcolonyoptimizationalgorithmforthebi-objectiveshortestpathproblem［J］．AppliedSoft

2010，10（4）：1237-1246Computing，

［28］FANGZHX，ZONGXL，LIQQ，etal．Hierarchicalmulti-objectiveevacuationroutinginstadiumusingantcolonyoptimization

J］．JournalofTransportGeography，2011，19（3）：443-451approach［

［29］XUJP，YANF，STEVENL．Vehicleroutingoptimizationwithsofttimewindowsinafuzzyrandomenvironment［J］．

InPress，CorrectedProof，Availableonline，2011（4）：20TransportationResearchPartE：LogisticsandTransportationReview，

［30］FEOTA，RESENDEMGC．Aprobabilisticheuristicforacomputationallydifficultsetcoveringproblem［J］．Operations

1989，8（4）：67-71ResearchLetters，

［31］RAFAELM，JOSLG，AbrahamDuarte．Heuristicsforthebi-objectivepathdissimilarityproblem［J］．Computers＆Operations

Research，2009，36（11）：2905-2912

［32］ANDRZEJJ，PIOTRZ．Paretomemeticalgorithmwithpathrelinkingforbi-objectivetravelingsalespersonproblem［J］．

EuropeanJournalofOperationalResearch，2009，193（3）：885-890

［33］王君，J］．计算机集成制造系统，2011，17（4）：858-866李波．带模糊预约时间的车辆路径问题的多目标禁忌搜索算法［

［34］OJHAA，DASB，MONDALS，etal．Anentropybasedsolidtransportationproblemforgeneralfuzzycostsandtimewithfuzzy

equality［J］．MathematicalandComputerModelling，2009，50（1-2）：166-178

［35］LASDONLS，WARENAD，JAINA，etal．Heuristicsforthebi-objectivepathdissimilarityproblem［J］．ACMTransactionson

1978，4（1）MathematicalSoftware，

［36］HORSTWH，STEFANR，STEVANUSAT．Algorithmsfortime-dependentbicriteriashortestpathproblems［J］．Discrete

Optimization，2006，3（3）：238-254

［37］ZAMIRIANM，KAMYADA，FARAHIM．Anovelalgorithmforsolvingoptimalpathplanningproblemsbasedonparametrization

methodandfuzzyaggregation［J］．PhysicsLettersA，2009，373（38）：3439-3449

［38］TRISTRAMG，ALAINB，YVESD．Timedependentmultiobjectivebestpathformultimodalurbanrouting［J］．ElectronicNotes

inDiscreteMathematics，2010，36（1）：487-494

84重庆工商大学学报（自然科学版）第29卷ReviewoftheAlgorithmsofMulti-objectiveRoutingProgrammingProblems

PANBin-bin

（SchoolofManagement，ChongqingJiaotongUniversity，Chongqing400074，China）

Abstract：Single-objectiveroutingoptimizationmodelisdifficulttosimulatecomplexandchangeablesituationinreallife，however，multi-objectiveroutingoptimizationismoreclosetoreality，hasmoreguidingsignificancetosolvingpracticalproblems，isahottopicintheresearchofcomputerscienceandlogisticsscienceandproducesalotofproducts．Inordertooverallsummarizetheresearchstatusquoofmulti-objectiveroutingoptimizationalgorithms，thispaperreviewstheapplicationofmulti-objectiveroutingoptimizationalgorithmsindifferentbackgroundsathomeandabroadanditsprogress，makescorrespondingclassificationaccordingtocomposingmethodsofthealgorithms，makessummarization，analyzestheexistedproblemsandproposesthedirectionforfurtherresearch．

Keywords：multi-objective；routingoptimization；NPproblem；exactalgorithm；heuristicalgorithm

责任编辑：代小红

櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍（上接第77页）

AMonitoringMethodforSQLServerSecurityBasedonC#

CHENJian-hua

（DepartmentofComputer，GuangdongSongshanVocationalCollege，GuangdongShaoguan512126，China）

Abstract：InordertoprotectthesecurityofSQLdatabaseserver，thispaperproposesakindofmonitoringmethodforSQLserversecuritybasedonC#torealizedynamicmonitoringonSQLSERVERdatabaseserverandtofindoutthesecuritystatusofSQLdatabaseserverthroughmonitoringthechangeofSQLdatabaseserverontime，analyzesthereasonsforthechangeandtakesmeasuresintimesothatthesecurityofSQLdatabaseserverisprotected．Anewideaonhowtoprotectthesecurityofdatabaseispointedoutbyusingprogramstorealizethe

whichisakindofcomplementandexpandingforsecuritymanagementandmonitoringandmanagementondatabase，

securityprotectionofdatabaseserviceandwhichisofimportantsignificanceinrealwork．

Keywords：SQLserver；databaseaccesscontrol；data-tablemonitoring

责任编辑：代小红

二 : 机器人路径规划概述

机器人路径规划[J].计算机工程与应用，2005，41(19)：59-60,82.

!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

(上接第4页)

仅成为军事上必不可少的电子装备，并且在洪水监测、海冰监测、土壤湿度调查、森林资源清查、地址调查等方面也显示了很好的应用潜力。用一部雷达代替多部雷达的功能，使一种雷达具有多种对抗能力，即多功能复合体制雷达[6]应是发展重点之一。参考文献

[1]丁鹭飞,耿富录,陈建春.雷达原理[M].北京：电子工业出

版社，2009.

[4]罗式胜.文献计量学引论[M].北京：书目文献出版社，

1987.

[5]GB7713-87.论文写作规范国家标准[S].

[6]邱荣钦.雷达技术的发展[J].电子科学技术评论，2005

(3):1-6.

(收稿日期：2010-10-19)

作者简介:

罗星华,女,1983年生,硕士,主要研究方向：信号与信息处理、信息服务、参考咨询、情报研究。

张碧锋，男，1983年生，硕士研究生，助理工程师，主要研究方向：信号与信息处理。

[2]吴顺君,梅晓春.雷达信号处理和数据处理技术[M].北

京：电子工业出版社，2008.

[3]陆莉.近20年来我国对东盟经济研究论文的统计分析

[J].现代情报,2008(2):209-212.

8

《微型机与应用》2011年第30卷第2期

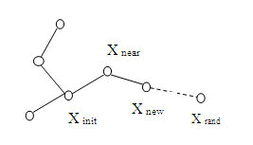
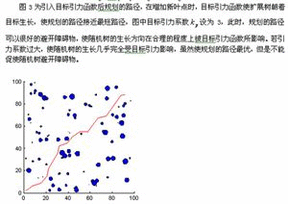
三 : 基于未知环境下改进的RRT路径规划算法

2013/5/23 14:04:05 供稿：孙丽娜，沈政军 打印

本文针对复杂环境下移动机器人的路径规划问题，在随机扩展树算法的基础上，结合势场法的目标引力函数，对原有算法进行了改进。改进后的算法能够引导新叶节点向目标方向扩展，减少了采样点的数目，大大缩短了规划时间，规划出的路径更接近最优或次优；同时，使机器人在执行同一任务的可重复性得到提高，路径也更加的光滑。大量的仿真实验结果表明，该算法显著提高机器人规划效率，具有较高的计算实时性，适合机器人实际应用。



摘 要：针对移动机器人运用快速扩展树(RRT)算法进行路径规划，随机性大的问题，提出了一种目标引力式的RRT路径规划算法。该算法在RRT算法的基础上，引入了一个目标引力函数，促使扩展随机树朝目标点方向生长。仿真结果表明，该算法提高了复杂环境下机器人路径规划的效率，能够得到接近于最短的路径，并对同一任务的规划具有一定的可重复性，能够安全的避开障碍物。

关键词：路径规划；快速扩展随机树(RRT)；目标引力函数

文献标识码：A 中图分类号： TP24

The Improved RRT Path Planning Algorithm Based on Unknown Environment

SUN Lina，SHEN Zhengjun

(College of Automation & Electronic Engineering，Qingdao University of Science and Technology, 266042, China)

Abstract: Aiming to solve the uncertainty using rapidly-exploring random tree (RRT) for path planning algorithm, an algorithm of mobile robot path planning based on target gravity is proposed. The algorithm introduces target gravitational function, which makes the random tree grow toward the target. Simulation results show that the algorithm improves path planning efficiency in the complex environment; the path is close to the shortest path, avoids obstacles safely and has a certain repeatability for the planning of same task.

Key Words: Path Planning; Rapidly-Exploring Random Tree (RRT); target gravitational function

路径规划技术是移动机器人研究领域的一个重要方面，主要解决如何在工作空间中找到一条从起始点到终点的最优路径，并在运动中能够安全无碰撞的绕过障碍物。在未知环境下，机器人没有先验知识，不能离线做出一次性的全局规划，只能依靠实时探测的局部环境信息规划局部路径，如何规划出全局路径且使路径较优，研究者已经提出了不少解决方法和策略[1,2]。然而，在环境趋于复杂或障碍物的数目增加时，如何避免震荡和死锁，如何使机器人所走路径全局最优或较优，仍是有待解决的问题。

快速扩展随机树（RRT）是目前应用比较广泛的基于采样的单查询运动规划方法，通过状态空间的随机采样点，把搜索导向空白区域，从而寻找一条从起点到目标点的路径规划，适合于复杂环境和变化场景的路径规划。但是RRT算法所具有的采样随机性，产生了路径规划实时性不高，在执行同一任务时可重复性比较差和很难规划出最优路径等问题。

目前RRT算法产生了许多改进，如具有启发式的RRT算法、基于滚动窗口的RRT算法等[3-5]，可是产生的路径存在绕远或者出现明显的拐角，使路径不平滑；或产生死锁振荡等。为此，本文引入人工势场法中的目标引力，使规划路径接近最优或次优，并改进了路径不平滑这一缺陷，通过合理的设置引力系数，克服了局部极小的问题。

1 RRT算法分析

RRT算法是以状态空间中的一个初始点作为根节点，用过随机采样扩展，逐渐增加叶节点，生成一个随机扩展树，当随机树的叶节点中包含了目标点或目标区域中的点时，从初始点到目标点之间的一条以随机树的叶节点组成的路径就是路径规划。





图1 RRT的构建

Fig.1 The RRT construction

由于RRT算法是按照树枝的生长路径进行规划，从而导致规划的路径有时接近最短路径，有时远离最短路径，缺乏光滑性，并对同一任务的规划缺乏可重复性。该算法具有很多的随机性，其本身所包含的一些缺点，对其在移动机器人中的应用产生了一定的限制。

2 改进的RRT算法

将人工势场法中的目标引力思想引入RRT算法，引导随机树朝着目标方向生长，大大减少规划时间,提高了算法的实时性保证了规划路径的最优性，改进路径不光滑的缺点，避免了产生局部极小，使算法在规划路径方面的能力得到很大的提高。



在通过RRT算法增加新叶节点时，目标引力函数会通过计算每个节点到目标的引力量来影响新节点的选取，引导随机树向目标方向生长。





图2 RRT算法规划的路径

Fig.3 The path planning for RRT algorithm



图3 算法改进后规划的路径

Fig.3 The path planning for improved RRT algorithm

仿真实验结果显示：通过合理地设置引力系数，使改进后的算法保留了RRT算法中向空旷地带搜索的特性，可以快速绕过障碍物找到可行路径，大大减少了不必要的扩展，提高了机器人运动的实时性，使生成的路径相对平滑，满足机器人机器人在复杂环境下的路径规划。

4结论

本文针对复杂环境下移动机器人的路径规划问题，在随机扩展树算法的基础上，结合势场法的目标引力函数，对原有算法进行了改进。改进后的算法能够引导新叶节点向目标方向扩展，减少了采样点的数目，大大缩短了规划时间，规划出的路径更接近最优或次优；同时，使机器人在执行同一任务的可重复性得到提高，路径也更加的光滑。大量的仿真实验结果表明，该算法显著提高机器人规划效率，具有较高的计算实时性，适合机器人实际应用。

参考文献

[1] 张纯刚,席裕庚.动态未知环境中移动机器人的滚动路径规划及安全性分析.控制理论与应用, 2003, 20(1): 37-44.

[2] 王丽.移动机器人路径规划方法研究[D].西北工业大学硕士论文.2007,3.

[3] 康亮,赵春霞,郭剑辉.未知环境下改进的基于RRT算法的移动机器人路径规划[J].模式识别与人工智能.2009,22(3)337-343.

[4] MelchiorNA, SimmonsR. Particle RRT for Path Planning with Uncertainty[J].Proc of the IEEE International Conference on Robotics and Automation. Roma, Italy, 2007:1617- 1624.

[5] 冯林,贾菁辉.基于对比优化的RRT路径规划改进算法[J].计算机工程与应用,2011,47 (3):210-213.

[6] 王滨,金明河,谢宗武等.基于启发式的快速扩展随机树路径规划算法[J].机械制造,2007, 45 (12):1-4.

[7] 宋金泽,戴斌,单恩忠等.一种改进的RRT路径规划算法[J].电子学报,2010,2A (38):225-228.

[8] 高云峰,黄海.复杂环境下基于势场原理的路径规划方法[J].机器人,2004,26(2):114-118

3仿真分析

四 : 多目标路径规划问题的算法综述_潘斌斌

第29卷第5期Vol.29NO．5重庆工商大学学报（自然科学版）JChongqingTechnolBusinessUniv.（NatSciEd）2012年5月May2012文章编号：1672－058X（2012）05－0078－07

多目标路径规划问题的算法综述

潘斌斌

（重庆交通大学管理学院，重庆400074）

摘要：单目标路径优化模型难以更好的模拟实际生活中复杂多变的状况，相比而言多目标路径优化更贴近于现实，对实际问题更具有指导意义，也是近年来计算机科学和物流科学研究的一个热点问题，产生了众多的研究成果；为全面总结多目标路径优化算法的研究现状，综述了国内外多目标路径优化算法在不同背景下的应用及取得的进展，并按算法的构造方法进行了相应的分类；最后进行了总结分析了存在的问题，并指明其进一步的研究方向。（www.61k.com）

关键词：多目标；路径优化；NP难题；精确算法；启发式算法

中图分类号：TP374文献标志码：A

1引言

路径规划问题指涉及在一个网络中，找出一条满足一系列约束的路线，且使一个目标或多个目标最优

包括著名的旅行商问题（TravelingSaleman化的一类问题。路径规划问题是一类被广泛研究的问题，

Problem，TSP）、VRP）、车辆路径规划问题（VehicleRoutingProblem，应急疏散路线设计、救济品及危险品运输路线设计、物流配送优化等。路径选择时，通常考虑单个目标（如成本最小化）进行优化，而实际生活中这类问题是一个复杂的多目标问题，确定性的单目标的路径优化已不能满足实际需求，能提供的意义是有限的，多目标路线规划模型能更好的贴近现实，具有重要的科研价值和实际意义。在物流业大力发展、城市交通规划的发展、绿色环保的倡导下及单目标路径优化的片面性，多目标的路径优化研究逐渐成为研究的热点。在此对多目标路径规划问题的算法进行了综述，并展望了研究前景。

2各种算法在多目标路线规划中的应用

一般情况下，多目标优化问题的各个子目标之间是矛盾的，一个子目标的改善有可能会引起另一个或另几个子目标的性能降低，即要同时使多个子目标一起达到最优值是不可能的，而只能在它们中间进行协调和折中处理，使各个子目标都尽可能地达到最优化。多目标优化问题不存在唯一的全局最优解，过多的非劣解是无法直接应用的，所以在求解时要寻找一个最终解。求最终解主要有三类方法［1］：（1）生成法，即

构成非劣解的一个子集，然后按照决策者的意图找出最终解；（2）交互法，不先求出很先求出大量的非劣解，

多的非劣解，而是通过分析者与决策者对话的方式逐步求出最终解；（3）权重法，其主旨是将所有的目标函

收稿日期：2011－08－21；修回日期：2011－09－27．

），作者简介：潘斌斌（1988-男，浙江省温岭市，硕士，从事供应链与企业物流管理研究．

路径规划 多目标路径规划问题的算法综述_潘斌斌

第5期潘斌斌：多目标路径规划问题的算法综述79数，依据其重要性乘以一个权值，然后求和，转化为单目标问题进行求解。(www.61k.com]而这些主要是通过算法来实现的。

大量文献分析表明：多目标路线规划问题的研究方法主要分为两大类，即精确算法和启发式算法。由于精确算法（如动态规划、整数规划等数学规划方法）难以解决大规模的复杂多目标路线规划问题，启发式优化方法在多目标路线规划问题研究中应用的较多。

2．1整数规划法

整数规划（integerprogramming）主要应用于规模有限的多目标路线规划问题上。其基本思路是首先分

Lingo等数学软件进行求解，析问题的特性，再构造出对应的整数规划模型，最后利用Matlab、可以直接给出

［2］路线的分配情况，但只有一个确定解。AlexanderStepanov等人在疏散路线的设计中利用整数规划进行求

［3］提出了多目标整数线性规划来进行集装箱供应链解。HUZhiHua针对集装箱多式联运紧急救济的网络，

的路径选择，将多个目标进行整合成单个目标，最后通过传统的软件包进行求实现时间及成本最小化。

2．2动态规划算法

动态规划算法（Dynamicprogramming）适用于解决那些可分解为重复子问题（overlappingsubproblems）并具有最优子结构（optimalsubstructure）的问题，通常比其他普通算法节约更多时间。动态规划算法通常采用以下两种方式：（1）自顶向下，将问题划分为若干子问题，求解这些子问题并保存结果以免重复计

该方法将递归和缓存结合在一起。（2）自下而上，先行求解所有可能用到的子问题，然后用其构造更算，

大问题的解。

KonstantinosN等［4］针对多目标路线规划问题，将问题分解为一系列路线子问题，通过动态规划算法进

［5］行求解。LineBlanderReinhardt等人针对条件和目标不可累加的多目标最短路问题，给出了一个通用的

最后用动态规划算法进行求解。公式来处理一系列不可累加的条件，

2．3启发式算法

多目标优化问题往往通过加权等方式转化为单目标问题，然后用数学规划的方法来求解，每次只能得

由于多目标优化问题的目标函数和约束函数可能是非线性或不可微到一种权值情况下的最优解。同时，

的，及随着问题规模的增大，问题的复杂度也相应增加，计算的时间也将呈指数级增加，影响了最优算法的效率。一般最优算法应用于数据规模较少的多目标路线规划问题中。对于涉及大规模的多目标路线规划问题，启发式算法（heuristicalgorithms）提供了一种效率较高的求解途径。

Jean-FrancoisBérubé等人［6］提出了将多个目标转化为解决一个单目标的子针对多目标的旅行商问题，

使所有目标转化为约束，并用基于可从前面子问题收集信息的启发式算法加快处理速度，解决了收集问题，

Juliane到奖金最大化且旅行费用最低的旅行商问题。针对双目标的带时间窗的车辆路径规划问题，

［8，9］Müller［7］提出了一种启发式算法，实现总的运输车辆数和运输距离最小。首先，利用Solomon提出的途程

再将途程改善启发式算法（RouteImprovement建构启发式算法（routeconstructionheuristic）得到初始解，

Heuristics）应用到当前解中减少车辆的数目和距离。以及在文献［10］11］和文献［中研究者针对多目标路径规划问题也提出了启发式算法进行求解。

2．4元启发式算法

heuristicalgorithms）是一种通用型的启发式算法，元启发式算法（meta-是对启发式算法的改进，优化机

理不过分依赖待解问题的结构，结合了随机方法和搜索算法。主要包括遗传算法（geneticalgorithm）、模拟退火算法（simulationannealingalgorithm）、禁忌搜索算法（tabusearchalgorithm）、粒子群算法（particleswarmoptimization）、蚁群算法（antcolonyalgorithm）、贪婪随机自适应搜索算法（GreedyRandomizedAdaptiveSearchProcedure）等。这些方法被逐渐引入到多目标路线规划问题研究中，并取得了一定的研究进展。

路径规划 多目标路径规划问题的算法综述_潘斌斌

80

2．4．1遗传算法重庆工商大学学报（自然科学版）第29卷

遗传算法（geneticalgorithm）是是一种借鉴生物界自然选择和进化机制发展起来的高度并行、随机、自适应搜索的仿真优化算法，它使用种群代表一组解，通过对当前种群进行选择、交叉和变异等一系列遗传操作，产生新一代种群，周而复始，直到满足终止条件得到包含近似最优解为止。[www.61k.com)

在多目标路线规划问题研究中，遗传算法往往通过以下方法对模型进行求解：与传统优化技术结合；将遗传算法同其他启发式方法相结合构造混合遗传算法来求解；模糊理论、权重法与遗传算法的结合。

P．Lacomme等人［12］受非支配排序遗传算法（Non-dominatedsorted在车辆路径规划问题（VRP）中，

［13］geneticalgorithm）的启发，构建了启发式算法来求解多目标的车辆路径规划问题。K．C．Tan等人提出了

该方法具有专用的遗传算子，可变长度的表示法和局部搜索启发式法来混合的多目标进化算法（HMOEA），

同时使路径距离和卡车数最小化的多目标问题。许国银等人求解决路线日程安排，［14］综合考虑战时配送

VRP（vehicleroutingproblem）的多个评价目标，基于重要性的多目标分层优化思想，建立了完全分层优化模

［15］将进化算法和传统优化技术相结合，构造了模型的两层求解算法。H．C．W．Lau等人考虑了多个仓型，

库、多个顾客和多种物品，为实现总的运输距离，总的运输时间最优，提出模糊理论指导的非支配排序遗传

NSGA2）的多目标进化算法。WANGChungHo等人［16］为使总的配送路线最小化及通过满足时间算法2（FL-

窗的要求使顾客对服务的满意度最大化，提出了基于贪婪算法、遗传算法的混合算法来求解多目标模型中

17-19］中，其他研究者也提出了基于遗传算法的元启发式算法。在旅行商问题中，的变量。以及在文献［

FundaSamanlioglu等人［20］提出了memeticrandom-key遗传算法。

在其他多目标路线优化问题中，井祥鹤等人［21］提出了一种求解多式联运运输方式选择多目标优化问题

［22］的混合遗传算法，给出了染色体编码、遗传算子设计、染色体有效性判断和修正的方法。林勇等人在解决

GA）中融入了NSGA-多目标运输优化问题的基于生成树的遗传算法（st-Ⅱ算法，提出了一种新的生成树遗

GA），采用精英保留和擂台法来进行遗传选择，算例结果表明新算法提高了收敛速度，防止了传算法（NSST-

23］早熟收敛，较好的保持了种群多样性和算法的稳定性。以及在文献［中，其他研究者也提出了基于遗传

算法的元启发式算法。

2．4．2蚁群算法

［24］蚁群算法（AntColonyOptimization）是一种新型的模拟进化算法，由M．Dorigo等人首先提出。与其他

元启发式算法不同，它采用分布构建解的流程，每只蚂蚁选择下一步时，需要参考整个种群的累积经验和启发式信息。ACO算法求解路径优化问题的流程［25］如下：（1）蚂蚁群体初始化；（2）循环以下过程直到满足

信息素挥发，可选的全局操作；（3）输出最优路径。终止条件：所有蚂蚁选路并释放信息素，

YUANYuan等人［26］针对危机物流管理问题，提出了一个多目标路径选择模型用来使沿通道转移的时

［27］间最小化和使路径复杂度最小化，并用蚁群算法进行了求解。KeivanGhoseiri等人针对多目标最短路问

题（MOSP），提出了一种基于多目标优化的蚁群算法（ACO）来解决双目标最短路问题。FANGZhiXiang等人［28］针对疏散路线的网络规划，提出了多目标优化来解决基于多层决策网络的疏散路线规划问题，最后利

粒子群算法用蚁群优化算法进行求解。2．4．3

粒子群算法（ParticleSwarmOptimization）和遗传算法相似，也是从随机解出发，通过迭代寻找最优解，但

不涉及交叉、变异操作，而是通过追随当前最优值来找到全局最优解。粒子群算在规则上比遗传算法简单，

［29］法应用于多目标路径规划的研究中的文献相对较少。XUJiuPing等人针对模糊随机环境下的带软时间

窗的车辆路径问题（VRPSTW）。考虑如下两个目标：总的运输费用最小化；使所有顾客的平均服务水平最大

PSO-EP）用来求解该问题。化。提出了可变粒子的全局-局部-邻近粒子群优化算法（GLN-

路径规划 多目标路径规划问题的算法综述_潘斌斌

第5期潘斌斌：多目标路径规划问题的算法综述81

2．4．5贪婪随机自适应搜索算法

［30］GRASP）是一种新的元启发式贪婪随机自适应搜索算法（GreedyRandomizedAdaptiveSearchProcedure，算法，主要包含贪婪函数、自适应过程、随机组成和局域搜索4个方面，由FEO等人提出。[www.61k.com）GRASP是一个

每次迭代过程包含两个阶段：构造阶段和局域搜索阶段。得益于GRASP在初始构造启发式随机迭代过程，

在计算速度上会比一般的启发式算法如遗传算法等快，随着问题规模的加大，阶段采取了适当启发式策略，

速度上的优势会比较明显。

RafaelMartí将GRASP应用与多目标路径优化研究方面的文献较少。在为危险物品选择交通路线时，

等人［31］介绍了一种双目标优化模型，提出了用改进的GRASP进行求解。RafaelMartí等人做的主要改进是

多目标遗传局部搜索算法将随机分解方法RDE融入到构造阶段而提出了改进的GRASP。2．4．6

多目标遗传局部搜索算法（Memetic算法）是求解多目标优化问题最有效地方法之一，融合了局部搜索和进化计算，具有较高的全局搜索能力。这种算法加强了搜索算法的目的性，加快了收敛到局部最优解的

［32］针对双目标的旅行商问题提出了融入Pareto局部搜索算法的Pareto速度。AndrzejJaszkiewicz等人

memetic算法，经实验证明该算法有效地改进了计算结果。

2．4．7禁忌搜索算法

［33］禁忌搜索算法（TabuSearchAlgorithm）是一种亚启发式搜索算法，从一个初始可行解出发，选择一系列的特定搜索方向（移动）作为试探，选择实现让特定的目标函数值变化最多的移动。王君等人

提出了多目标禁忌搜索算法。模糊预约时间的多目标车辆路径问题，

2．5其他方法

（1）Zimmermann方法（模糊多目标线性规划）和广义简约梯度算法。考虑不精确的单位费用和路线方

A．Ojha等人［34］依据Zimmermann方法和模糊等价面的运输时间（广义模糊数）的多目标多模式运输问题，

性措施将多目标优化减少到单目标优化问题，然后利用广义简约梯度算法

找到最优的解决方案。

（2）反向演算法。针对基于时间的双标准最短路问题（TdBiSP），HorstW．Hamacher等人［36］提出了反向演算法进行求解。

（3）整合参数化方法和模糊聚类方法。模糊聚类方法是以隶属度作为聚类的出发点，以模糊等价矩阵

［37］提出了整合参作为启发规则的算法。PhysicsLettersA等人针对多目标动态优化的最优化路径规划问题，［35］在针对带（GRG）用来从一大堆数据中

数化方法和模糊聚类方法进行求解。

（4）Martin算法。TristramGrbener等人［38］针对基于时间的多目标最优路径提出Martin算法进行求解。

3结束语

虽然多目标路径规划问题的研究已取得了一定的研究成果，但由于在这一领域的大部分问题都没有唯一的全局最优解且具有NP难题特性，而各种算法又都有其自身的缺陷，至今尚未有非常高效的解决方法和理论。通过对路径规划领域的多目标优化算法的综述，归纳了多目标路径优化算法的几个未来研究方向：

（1）文献中研究的大部分多目标路径优化问题基于静态环境下的居多，难于应用与现实中复杂多变的环境。相对静态环境下的多目标路径优化问题，动态环境下的多目标路径优化问题更贴近实际应用。如时变环境下的多目标路径优化将是未来研究的重点。

路径规划 多目标路径规划问题的算法综述_潘斌斌

82重庆工商大学学报（自然科学版）第29卷

（2）与精确算法相比，元启发式算法尽管相对简单、灵活，计算效率高，但不一定能保证所得解的可行性和全局最优性，甚至在多数情况下，无法分析所得解同最优解的近似程度。（www.61k.com］因此，为了克服各种元启发式算法的缺点和发挥其各自的优势，将两种或两种以上启发式算法结合起来形成更加高效的混合智能启发算法，将是多目标路径优化算法研究的重要方向之一。

（3）多目标优化问题难以找到一个最优解，大多是在各个目标间权衡、协调寻求一个折中解。而将模糊

能够较好的考虑不同性质的、相互矛盾的多个目标的满意程度，使各个目标理论引入到多目标规划问题中，

在约束条件下都最大程度地实现。为解决多目标优化问题提供了新的途径，如模糊理论指导下的遗传算法等将成为未来多目标路径优化算法的研究的一个热点。

参考文献：

［1］肖晓伟，J］．计算机应用研究，2011，28（3）：805-808肖迪，林锦国，肖玉峰．多目标优化问题的研究概述［

［2］ALEXANDERS，JAMESM．Multi-objectiveevacuationroutingintransportationnetworks［J］．EuropeanJournalofOperational

Research，2009，198（2）：435-446

［3］HUZHH．Acontainermultimodaltransportationschedulingapproachbasedonimmuneaffinitymodelforemergencyrelief［J］．

2011，38（3）：2632-2639ExpertSystemswithApplications，

［4］KONSTANTINOSN，ANDROUTSOPOULOSK．Solvingthemulti-criteriatime-dependentroutingandschedulingproblemina

multimodalfixedschedulednetwork［J］．EuropeanJournalofOperationalResearch，2009，1（1）：18-28

［5］LINEBR，DAVIDP．Multi-objectiveandmulti-constrainednon-additiveshortestpathproblems［J］．Computers＆Operations

2011，38（3）：605-616Research，

［6］JEANn-FRANOISRUB，MICHELG，JEAN-YVESP．Anexactε-constraintmethodforbi-objectivecombinatorialoptimization

J］．EuropeanJournalofOperationalResearch，2009，194problems：ApplicationtotheTravelingSalesmanProblemwithProfits［

（1）：39-50

［7］JULIANEM．ApproximativesolutionstothebicriterionVehicleRoutingProblemwithTimeWindows［J］．EuropeanJournalof

OperationalResearch，2010，202（1）：223-231

［8］MARIUSM．Algorithmsforthevehicleroutingandschedulingproblemswithtimewindowconstraints［J］．OperationsResearch，

1987，35（2），254-264

［9］MARIUSM，JACQUESD．Timewindowconstrainedroutingandschedulingproblems［J］．TransportationScience，1988，22（1），

1-13

［10］CHANGT．Bestroutesselectionininternationalintermodalnetworks［J］．Computers＆OperationsResearch，2008，35（9）：

2877-2891

［11］CARAMIAM，GUERRIEROF．Aheuristicapproachtolong-haulfreighttransportationwithmultipleobjectivefunctions［J］．

EuropeanJournalofOperationalResearch，2009，37（3）：600-614

［12］LACOMMEP，PRINSC，SEVAUXM．Ageneticalgorithmforabi-objectivecapacitatedarcroutingproblem［J］．Computers＆

OperationsResearch，2008，35（9）：3473-3493

［13］TANKC，CHEWYH，LEELH．Ahybridmulti-objectiveevolutionaryalgorithmforsolvingtruckandtrailervehiclerouting

problems［J］．EuropeanJournalofOperationalResearch，2006，172（3）：855-885

［14］许国银，J］．解放军理工大学学报：自然科学版，2007，熊孝和，林涛．基于GASA算法的成品燃油战时公路配送路径优化［

8（2）：180-185

［15］LAUHCW，CHANTM，TSUIWT，etal．Afuzzyguidedmulti-objectiveevolutionaryalgorithmmodelforsolvingtransportation

problem［J］．ExpertSystemswithApplications，2009，36（4）：8255-8268

［16］WANGC，LIC．Optimizationofanestablishedmulti-objectivedeliveringproblembyanimprovedhybridalgorithm［J］．Expert

SystemswithApplications，2011，38（4）：4361-4367

路径规划 多目标路径规划问题的算法综述_潘斌斌

第5期潘斌斌：多目标路径规划问题的算法综述83［17］NICOLASJ，FRDRICS，El-GHAZALIT．Anevolutionaryalgorithmforthevehicleroutingproblemwithroutebalancing［J］．

Computers＆OperationsResearch，2009，195（3）：761-769

［18］KEIVANG，SEYEDF．Multi-objectivevehicleroutingproblemwithtimewindowsusinggoalprogrammingandgeneticalgorithm

［J］．AppliedSoftComputing，2010，10（4）：1096-1107

［19］徐慧英，J］．计算机工程与科学，2010，32赵建民，张泳，朱信忠．改进NSGAII算法在车辆路径多目标优化问题中的应用［

（10）：117-121

［20］FUNDAS，WILLIAMG，FERRELLJ，etal．Amemeticrandom-keygeneticalgorithmforasymmetricmulti-objectivetraveling

J］．Computers＆IndustrialEngineering，2008，55（2）：439-449salesmanproblem［

［21］井祥鹤，J］．计算机工程与应用，2008，44（6）：210-212魏冬峰，周献中．运输方式选择多目标优化问题的混合遗传算法［

［22］林勇，GA遗传算法在多目标运输问题中的应用［J］．西南民族大学学报：自然科学版，2009，35张洪伟，沈哲宇．改进ST-

（6）：1161-1164

［23］高庆春，J］．信息技术，2010，5（28）：38-38韩应征，张立毅．军事应急物流中多目标路径优化的研究［

［24］DORIGOM，MANIEZZOV，COLORNIA．Theantsystem：Optimizationbyacolonyofcooperatingagents［J］．IEEE

Man，andCyberneticsPartB，1996，26（1）：29-41TransactionsonSystems，

［25］DORIGOM，MANIEZZOV，COLORNIA．Antcolonyoptimizationanewmeta-heuristic［J］．EvolutionaryComputation．1999：

1470-1477

［26］YUANY，WANGD．Pathselectionmodelandalgorithmforemergencylogisticsmanagement［J］．Computers＆Industrial

2009，56（3）：1081-1094Engineering，

［27］KEIVANG，BEHNAMN．Anantcolonyoptimizationalgorithmforthebi-objectiveshortestpathproblem［J］．AppliedSoft

2010，10（4）：1237-1246Computing，

［28］FANGZHX，ZONGXL，LIQQ，etal．Hierarchicalmulti-objectiveevacuationroutinginstadiumusingantcolonyoptimization

J］．JournalofTransportGeography，2011，19（3）：443-451approach［

［29］XUJP，YANF，STEVENL．Vehicleroutingoptimizationwithsofttimewindowsinafuzzyrandomenvironment［J］．

InPress，CorrectedProof，Availableonline，2011（4）：20TransportationResearchPartE：LogisticsandTransportationReview，

［30］FEOTA，RESENDEMGC．Aprobabilisticheuristicforacomputationallydifficultsetcoveringproblem［J］．Operations

1989，8（4）：67-71ResearchLetters，

［31］RAFAELM，JOSLG，AbrahamDuarte．Heuristicsforthebi-objectivepathdissimilarityproblem［J］．Computers＆Operations

Research，2009，36（11）：2905-2912

［32］ANDRZEJJ，PIOTRZ．Paretomemeticalgorithmwithpathrelinkingforbi-objectivetravelingsalespersonproblem［J］．

EuropeanJournalofOperationalResearch，2009，193（3）：885-890

［33］王君，J］．计算机集成制造系统，2011，17（4）：858-866李波．带模糊预约时间的车辆路径问题的多目标禁忌搜索算法［

［34］OJHAA，DASB，MONDALS，etal．Anentropybasedsolidtransportationproblemforgeneralfuzzycostsandtimewithfuzzy

equality［J］．MathematicalandComputerModelling，2009，50（1-2）：166-178

［35］LASDONLS，WARENAD，JAINA，etal．Heuristicsforthebi-objectivepathdissimilarityproblem［J］．ACMTransactionson

1978，4（1）MathematicalSoftware，

［36］HORSTWH，STEFANR，STEVANUSAT．Algorithmsfortime-dependentbicriteriashortestpathproblems［J］．Discrete

Optimization，2006，3（3）：238-254

［37］ZAMIRIANM，KAMYADA，FARAHIM．Anovelalgorithmforsolvingoptimalpathplanningproblemsbasedonparametrization

methodandfuzzyaggregation［J］．PhysicsLettersA，2009，373（38）：3439-3449

［38］TRISTRAMG，ALAINB，YVESD．Timedependentmultiobjectivebestpathformultimodalurbanrouting［J］．ElectronicNotes

inDiscreteMathematics，2010，36（1）：487-494

路径规划 多目标路径规划问题的算法综述_潘斌斌

84重庆工商大学学报（自然科学版）第29卷ReviewoftheAlgorithmsofMulti-objectiveRoutingProgrammingProblems

PANBin-bin

（SchoolofManagement，ChongqingJiaotongUniversity，Chongqing400074，China）

Abstract：Single-objectiveroutingoptimizationmodelisdifficulttosimulatecomplexandchangeablesituationinreallife，however，multi-objectiveroutingoptimizationismoreclosetoreality，hasmoreguidingsignificancetosolvingpracticalproblems，isahottopicintheresearchofcomputerscienceandlogisticsscienceandproducesalotofproducts．Inordertooverallsummarizetheresearchstatusquoofmulti-objectiveroutingoptimizationalgorithms，thispaperreviewstheapplicationofmulti-objectiveroutingoptimizationalgorithmsindifferentbackgroundsathomeandabroadanditsprogress，makescorrespondingclassificationaccordingtocomposingmethodsofthealgorithms，makessummarization，analyzestheexistedproblemsandproposesthedirectionforfurtherresearch．

Keywords：multi-objective；routingoptimization；NPproblem；exactalgorithm；heuristicalgorithm

责任编辑：代小红

櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍櫍（上接第77页）

AMonitoringMethodforSQLServerSecurityBasedonC#

CHENJian-hua

（DepartmentofComputer，GuangdongSongshanVocationalCollege，GuangdongShaoguan512126，China）

Abstract：InordertoprotectthesecurityofSQLdatabaseserver，thispaperproposesakindofmonitoringmethodforSQLserversecuritybasedonC#torealizedynamicmonitoringonSQLSERVERdatabaseserverandtofindoutthesecuritystatusofSQLdatabaseserverthroughmonitoringthechangeofSQLdatabaseserverontime，analyzesthereasonsforthechangeandtakesmeasuresintimesothatthesecurityofSQLdatabaseserverisprotected．Anewideaonhowtoprotectthesecurityofdatabaseispointedoutbyusingprogramstorealizethe

whichisakindofcomplementandexpandingforsecuritymanagementandmonitoringandmanagementondatabase，

securityprotectionofdatabaseserviceandwhichisofimportantsignificanceinrealwork．

Keywords：SQLserver；databaseaccesscontrol；data-tablemonitoring

责任编辑：代小红

本文标题：路径规划-多目标路径规划问题的算法综述_潘斌斌
本文地址： http://www.61k.com/1144571.html