一 : 秒差距的定义

秒差距的定义

什么是秒差距

秒差距的定义的参考答案

秒差距（英文Parsec,缩写pc）是天文学上的一种长度单位.秒差距(parsec)是一种最古老的,同时也是最标准的测量恒星距离的方法.它是建立在三角视差的基础上的.以地球公转轨道的平均半径（一个天文单位,AU）为底边所对应的三角形内角称为视差.当这个角的大小为1秒时,这个三角形（由于1秒的角的所对应的两条边的长度差异完全可以忽略,因此,这个三角形可以想象成直角三角形,也可以想象成等腰三角形）的一条边的长度（地球到这个恒星的距离）就称为1秒差距.

二 : 秒差距的计算

2014年宁波创新班考试科学试题中出现一道关于秒差距的单位，在诸多科学教师中引起反响。一、对于习惯于“光年”“天文单位”的天文学的长度单位而言，秒差距具有一定的陌生程度，很新颖。二、对于秒差距的计算却有着较多的困惑，是考查学生数学能力还是分析能力？

【原题】秒差距是古老的天文学上的一种长度单位。从地球公转轨道的平均半径为底边所对应的三角形内角称为视差，当这个角的大小为1角秒（角秒就是秒，1度等于60分，1分等于60秒）时，这个三角形（由于1秒的角所对应的两条边长度差异可以忽略，这个三角形可以看成等腰三角形）的一条边的长度就称为1秒差距（即为太阳到恒星的距离）。你估计“1秒差距”约为多少光年？（结果保留一位有效数字，1天文单位为1.5×10⁸km）▲

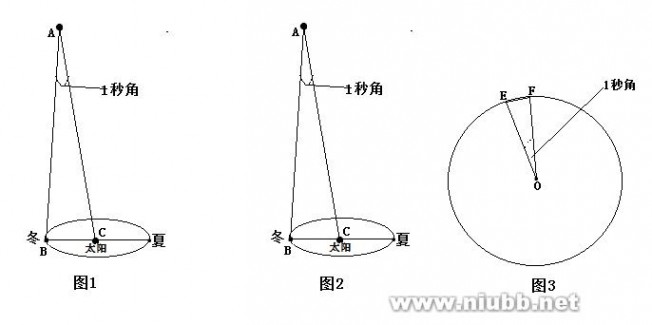
解法一：如图1

由于AB、AC两边相差不大，因此可以将△ABC近似看成直角三角形，∠ABCA=90°。那么恒星到太阳的距离AC就等于BC/sin∠BAC。又由于∠CAB=1″，对于θ≦1°时有sinθ≈θ（其中θ为弧度制），因此有：

解法二：如图2、图3

由于由于AB、AC两边相差不大，因此可以将△ABC近似看成等腰三角形。在地球轨道圆内选定1秒角圆心角所对三角形△OEF，因为△ABC与△OEF为顶角相等的两等腰三角形，所以该两三角形相似，所以有BC/AC=EF/FO。由于角度很小的圆心角所对弦长与弧长近似相等，因此：

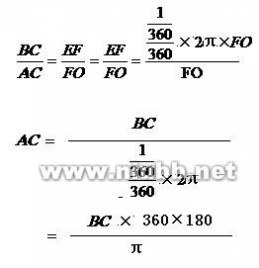
两种解法中无论哪一种都要用到近似处理，无论三角函数，还是相似三角形都需要较强的数学基础和数学能力，而这种计算似乎对科学素养的考察并不很强。

三 : 秒差距：秒差距-基本简介，秒差距-历史

秒差距（英文Parsec，缩写pc）是天文学上的一种长度单位。秒差距是一种最古老的，同时也是最标准的测量恒星距离的方法。它是建立在三角视差的基础上的。从地球公转轨道的平均半径（一个天文单位，AU）为底边所对应的三角形内角称为视差。当这个角的大小为1秒时，这个三角形（由于1秒的角的所对应的两条边的长度差异完全可以忽略，因此，这个三角形可以想象成直角三角形，也可以想象成等腰三角形）的一条边的长度（地球到这个恒星的距离）就称为1秒差距。

秒差距_秒差距 -基本简单介绍

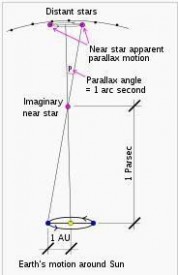秒差距

秒差距，Parsec，做为天文学的1个长度单位。听上去，秒，多么微小的单位，在时间上是不过是1个眨眼的瞬间。而在计算距离时的秒差距却是非常让人吃惊的数值了。

秒差距（英文Parsec, 缩写pc）是天文学上的1种长度单位。 秒差距(parsec)是1种最古老的，同时也是最标准的测量恒星距离的方法。它是建立在三角视差的基础上的。

以地球公转轨道的平均半径（1个天文单位，AU）为底边所对应的三角形内角称为视差。当这个角的大小为1角秒时，这个三角形（由于1秒的角的所对应的两条边的长度差异完全可以忽略，因此，这个三角形可以想象成直角三角形，也可以想象成等腰三角形）的一条边的长度（地球到这个恒星的距离）就称为1秒差距。

秒差距_秒差距 -历史

1个对象的第1个直接测量在跨星距离被承担了德语天文学家FriedrichWilhelm贝赛尔1838年，使用地球的轨道宽度作为基础线计算距离61Cygni使用位差并且三角学.星的位差是一半角距星看上去移动相对天体地球轨道在附近太阳;或者，相互地，它是角度对向从那个星的透视，由地球的轨道的半主要轴。对秒差距的用途作为距离单位从这个方法自然地跟随，因为距离(在秒差距)简单地是相互位差角度(在弧度秒)。即它是地球的轨道半主要轴将对向一秒角度弧的距离。

虽然它大概使用了前面，1913年期限秒差距是最初提起的在天文学出版物，当天文学家皇家坦率的华森Dyson表达了他的关心为名字的需要对距离那个单位：他提出名字astron，但提及那卡尔Charlier建议了siriometer和赫伯特?霍尔?特纳建议了秒差距(同水准-allax秒-ond)。

秒差距_秒差距 -数学计算

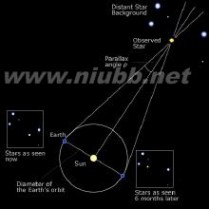秒差距

周年视差π = 1''的恒星与地球的距离r为206265AU（=3.08568×10^16 m = 3.2616 光年），这个距离定义为1秒差距（1pc）。天文学家通

常使用秒差距而不是天文单位来描述天体的距离。

这不仅是因为使用秒差距数字小更易于计算，而且还有历史上的原因。 天体的视差越大，则其距离就越近。反之，则视差越小，离我们越远。离我们最近的恒星（太阳除外）比邻星的秒差距约为1.29pc（4.22光年）。一秒差距等于30856775814913672.789米。 1秒差距=3.26156377716743356光年=206264.80624709635515647天文单位=308567.758亿公里。

验证：

在高等数学中，当θ 角（单位为弧度）→0时，sin θ → θ

1''=2π/（360*3600）（弧度）

1AU/1pc = sin 1'' ≈2π/(360*3600)

1pc=1AU/[2π/(360*3600)]=(360*3600/2π)*AU ≈ 206265AU，而1Au=1.496*10^8km，

因此，206265Au=3.08572*10^13km，1光年=365*24*3600*300000=9.4608*10^12km,

所以，1Pc/1光年=3.08572*10^13/9.4608*10^12=3.2616，即1pc=3.2616光年

如果周年视差分别为0.1角秒，0.01角秒，0.1角秒：

0.1角秒：秒差距=1Au/0.1角秒（弧）=10Au/1角秒（弧）=2062650Au=10Pc=32.616（光年）

0.01角秒：秒差距=1Au/0.01角秒（弧）=20626500Au=100PC=326.16（光年）

0.001角秒:秒差距=1Au/0.001角秒（弧）=206265000Au=1000PC=3261.6（光年）

很显然，秒差距是周年角秒视差的倒数的与1秒差距的乘积，大于1角秒同样适用。

秒差距_秒差距 -?应用

日常生活中我们有这样的经验：当我们移动自己的视线时，与自己远近不同的物体会出现移位，越近移得越大，越远移得越少，因此利用这个位差我们也可以推算出物体的距离。天文学家利用这种位差对天体的距离进行了量度，虽然恒星离我们的距离很远，地球的轨道相对于这个距离实在是微不足道，但遥远的恒星仍有我们肉眼无法感觉的位差，这个位差的小到我们要用圆面弧度上的秒来作单位，在地球轨道两侧相对的距离上，如果一颗天体在天球上移动的位差为一秒的话，这个天体离我们的距离天文学家就命名为“1秒差距”，大致为3.26光年。

本文标题：秒差距-秒差距的定义
本文地址： http://www.61k.com/1139501.html