一 : 排列组合的求和公式
1、等比数列
(1)等比数列:An+1/An=q,n为自然数.
(2)通项公式:An=A1*q^(n-1);
推广式:An=Am*q^(n-m);
(3)求和公式:Sn=nA1(q=1)
Sn=[A1(1-q)^n]/(1-q)
(4)性质:
①若 m、n、p、q∈N,且m+n=p+q,则am·an=ap*aq;
②在等比数列中,依次每 k项之和仍成等比数列.
(5)“G是a、b的等比中项”“G^2=ab(G≠0)”.
(6)在等比数列中,首项A1与公比q都不为零.
注意:上述公式中A^n表示A的n次方.
2、等差数列
Sn=(a1+an)n/2
Sn=na1+n(n-1)d/2
3、其他数列
对于这些数列没有特定的公式,但是一般都可以化为等比或等差数列求解.另外还有一些数列有特殊的求解方法可以让整个过程变得非常简单,这些需要自己在学习过程中慢慢总结.
二 : 在未来的某一天,会不会所有音符的排列组合方式都被用
【马小褂的回答(258票)】:
Update:更新科幻小说《忧郁的大象》翻译:忧郁的大象 - Magnil的博客 ,推荐给所有对此问题感兴趣的人。
另外,在其他人的答案和评论中,我看到了一些不同的意见,例如“无限猴子不适用于该问题”、“无论排列出多少种组合,随意加上一个音符又是新的排列”、“虽然当前音符是有穷的,但是音调还可以划分的更为细致,更何况还有音量和音色”等等。我觉得争议在于如何定义新音乐,即:两首歌要有多大程度上的区别,才可以称得上是不同的音乐?我补充了一小节内容对此加以说明。
相关链接请参考我的博客:音乐可能被穷尽吗?
-------------------------------------------------
很有趣的话题。前不久Youtube正好有这样一个科普视频,既然有人问了,我就翻译一下来回答楼主。

知乎用户的回答(258票):
嗯……假设,我们只用8个音符,全部都是单音吧(不考虑和弦),并且不把变奏和曲式变化算成两首不同的乐曲,并且假设一段乐曲还只有50个音符的情况吧。
这种情况下排列组合的结果一共大约是 14后面加44个0 种组合。假设每天地球上有其中的一亿种被占用的话(实际上这还蛮困难的,毕竟人类总数超过一亿的历史也并不太长),大约要14后面加32个0天才能用光这些组合。
顺便,已知宇宙的寿命大概是5后面加12个0天,也就是说……要用光这些排列组合,还需要人类日以继夜地做出更艰苦卓绝的努力才行。
【chenta的回答(6票)】:
「音符」本身就是无穷尽的,音乐不是只有 CDEFGAB 十二平均律这一种律制产生的排列组合,比如 微分音音樂,频谱作曲 Spectral music。
随着时代的发展,音乐当然也在发展。早在上个世纪作曲家们就不满足于只能用十二个音的大小调体系来写作,不断地在探寻和发明新的声响。
【匿名用户的回答(5票)】:
补充一下,排列组合可以给出不同音乐种类的的上限,但是要成为有意义的音乐还有符合一些其他基本规律, 比如说旋律节奏之类。而且人脑可区分的音乐数量大概更加有限。
【山鸡公子的回答(7票)】:
理论上也不能穷尽所有音乐作品
上面已经有人给出证明了,我补充几句。
很多人提到了《诗云》和无限猴子实验,颇有误导人之嫌。
《诗云》里的高级文明可以”写“出所有律诗和绝句,仅仅因为律诗和绝句有字数限制。
猴子有可能打出莎士比亚的作品,仅仅因为莎翁作品的长度是有限的。
让我们问另外两个问题:
《诗云》里的高级文明能在理论上写出包括现代诗在内所有的”诗“吗?如果你不给这个”诗“限定一个长度,神也不能。原因:整数是无穷大的。
猴子能写出所有理论上可能的戏剧吗?如果你不给戏剧限定一个长度,神也不能。原因:整数是无穷大的。
现在看音乐。音乐的情况更复杂,音乐也存在一个长度问题,如果音乐没有长度限制,便也不能穷尽。这点已经有匿名高人用简单的一句话指出:等排列完了告我一声,再加个哆,又是个新的排列。
一语中的。
那么如果我们限定音乐长度呢?我们仍然不能像穷尽文学作品那样穷尽音乐。为什么呢?决定一首音乐与另一首音乐不同的因素有很多。简单举几个:音乐由”音“构成,音有高低、强弱、长短、音色之分,我们将其称为“变量“。
当这些变量无界时,情形更刚才的”长度问题“相似,音乐无穷多。
假设这些变量全部有界,这个时候,音乐仍然是无穷多的,因为:这些变量跟文字不同,它们是连续的!因为变量的连续,音乐作为变量的函数,你就不可能穷尽所有理论上的音乐。这点也有高人指出了,引用:
chenta
「音符」本身就是无穷尽的,音乐不是只有 CDEFGAB 十二平均律这一种律制产生的排列组合,比如 微分音音樂,频谱作曲 Spectral music。 引用完毕。
为什么因为连续而不能穷尽呢?也有高人用简单的例子说明了,引用:
达达,精神病前期
……
但是我后来思考了一下,如果把这个当做一道数学题来计算的话,有一个漏洞:钢琴虽然只有88个按键,但不表明声音的高低真的是有限的,既然在CDEFGAB之外还有highCDEFGAB,那么随着科技发展就会有更先进的乐器能演奏出high highCDEFGAB,或者在do和升do之间再准确创造出一个“四分之一do”这样的概念,如同在1和1.5之间创造出1.25,那么从数学角度便开始讲不通了,因为数字是无穷的。 引用完毕
达达同学这还只是在讨论音高,一个音高就足够让音乐变得无穷多了,如果我们再加上其他同样具有连续性质的因素呢?
通过以上讨论我们可以证明:音乐的潜在数量是无穷的。
且慢:音高自然可以无限地细分,但人类对音的辨别能力是有限的。拿达达提出的例子来说,”四分之一do”也许是我们可以识别,但“六十八分之一do”人类就未必能识别了,数学的连续性在人类认知的领域里被打破。所以,决定音乐与音乐不同的因素在人类听来不再是连续,而是离散的。
结论可以是很繁琐的:
理论上的情形:当决定音乐的因素无界时,音乐无穷多;
做一定限制的理论上的情形:当决定音乐的因素有界而连续时,音乐无穷多;
更符合人类听力能力的情形:当决定音乐的因素有界而离散时,音乐有限。
结论也可以是简单的一句话:
音乐的世界是无限的,只可惜我等凡人无缘享受
知乎用户的回答(258票):
死理性派实在是忍不了不答不行:
首先,乐谱如果是白纸黑字的数字电路音乐家的演奏就像是微妙的模拟电路,演绎个千百遍,遍遍各不同。
其次,光就乐谱而言,以标准钢琴为例总共有88键, 52个白键,36个黑键。
单个音符就有88种可能。
一个小节内按时值不同可以划分为全音符、二分、四分、八分、十六分、三十二分、六十四分和一百八十二分音符。

光算一百八十二分音符总共有
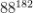
种possibility。
然后加上左手伴奏再乘以二有
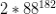
种possibility。
一首曲子一般都有一百来个小节,也就是说
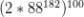
种。
上述都是作了简化处理,所以实际情况中通常一首两页的曲子有不少于((2* 88)^182 )^100种情况。
这个数字是多少?很抱歉,目前地球上还没有超级计算机能够胜任这个运算。负责任一点的计算器直接告诉你这个数已经代表无限种排列组合。

这还没算上休止符和附点音符的情况,音乐,具有无限可能。
钢琴_百度百科
音符_百度百科
【黄俊杰的回答(12票)】:
题主,您这个问题其实是很著名的思想实验“无限猴子”实验。无限猴子定理
这个思想实验是指,无限生命的猴子按无限个字符时,产生的乱码里会不会有莎士比亚的著作。若果是,那么当资源无穷是,是不是必然能造一个莎士比亚。
这个思想实验的变种,著名的有刘慈欣的《诗云》。这是个关于外星人试图穷尽汉字来写唐诗以说明人类是蝼蚁但最终失败的例子。
理论上来说答案都是“能”。哲学家大多论证为不能。
【李如春的回答(4票)】:
音乐的概念本身是在发展之中的,是个只要人类不消失,音乐概念的发展就不会停止,因此人类不灭、音乐不可能穷尽。
即使现有的音乐概念中,可以肯定的说,这样的情况也不会发生。音乐是不可能被穷尽的。题主貌似还不了解音乐的构成。音乐有单声部、多声部音乐之分。多声部音乐又有复调、主调与复调主调结合的类别。多声部的声部数量不定。
就单声部来讲,音乐不仅是音高的组合,构成音乐的要素有很多,比如节奏,同样的其它要素不变,节奏变化就可以令音乐形象大变,而节奏变化是无穷的。比如调式、调性、速度、节拍、力度、织体、音色、演奏法、律制等等都可以改变音乐。
重要的是好的音乐都是个自身独立的系统,即使大家都只用七个音,也可以赋予同一个音不同的意义----音乐的音在不同组合下价值与意义不同,看上去是同样的,但其实不一样。比如c这个音,可以是C大调主音,也是G大调下属音,a羽调宮音等等等等。如果在d的周围它是低的,在B的周围他是高的等等等等。
更不用说多声部音乐不同的和声、对位、配器啦。
明白音乐的奥妙了就不会有这样的疑问了。
【曾琪的回答(1票)】:
排列组合一下就知道完全用不完。
【张迪的回答(1票)】:
上面有人说了刘慈欣的《诗云》
这里展开讲一下吧。
《诗云》这个故事说的是,一个高等文明对地球的诗词很感兴趣,于是也想遣词造句。他用了一种方法,那就是把汉字按照诗词格律把所有可能的排列组合方式都排出来。里面必然包含了所有可能的优美诗词。但是这种排列组合的信息量太大,以至于要动用整个太阳系(也可能是什么xx天文单位之内)的所有的物质来制造信息储存装备(大概就是个超级文明的大U盘吧),按照现有物质的最大的信息储存效率,也消耗巨甚。
大至如此,细节记得不太清楚了。
反正就是说,哪些排列组合的信息量之大,不是人类能够理解的。
【匿名用户的回答(3票)】:
等排列完了告我一声,再加个哆,又是个新的排列。
【谷思洋的回答(0票)】:
Besides,
乐曲除了有音高和节奏的变化,还有强弱技巧等等N多N多方面的特征
就同一首曲子也能搞成完全不一样的面貌
不要低估作曲家疯狂的大脑
知乎用户的回答(258票):
我认为不会.因为快用完的时候,每次发现新的乐曲需要的时间更长
【高慜劼的回答(0票)】:
你是说在柯南小学毕业以前用完吗
【陈捷的回答(0票)】:
经典作品只听一秒你就能分辨出来是哪首,这就是音色。而音色是无法简单复制的。
【Eric的回答(0票)】:
想法不错,但是这个里面有个致命的问题,就是如何去衡量所谓的相识。 这个非常难界定,即使无视音色,音量,音高(在什么调上)。而仅仅是乐谱的画,这个也是无限的。因为音乐是一个过程, 从时间角度上看它就可以有无限的变化。但是如果仅仅是从音乐的一些单位上看,比如旋律1 23 4 32.
这个可能被用无限次,或者和弦走势,都是很快就能被穷尽的。不过从这个角度上来看,给与这样一个命题,以一个段落为单位(就像一首限定的4言绝句)那是可能很快就用完了,除开完全不和乐理或习惯的排列。遗憾的是满足上句的排列估计占所有排列的千分之一不到。
说道这个我也不得不提一下巴洛克音乐了,可以说现在的音乐都是巴洛克音乐的简化,那个时代其实已经用掉几乎所有可能的音符组合了。特别是巴赫的音乐,他自己的1000多作品近乎就占据了所有调性音乐可能的旋律组合(非调性音乐如各国民乐,爵士乐,非音乐)
话说回来,我应该可以写个随机程序播放中国民乐。
--by minhao xi
知乎用户的回答(258票):
从本质上来看,音乐是人类表达感受的形式。人类的感受是无穷的,在这一强大需求的推动下,会产生各种各样形式的音乐。你现在所想象的乐曲或许会被穷尽,但超越你所能想象形式的乐曲会出现。
【TomHall的回答(0票)】:
如果题主不嫌麻烦,可以来看看这篇短文~
不可思议的箱子:你的一生就在里面
【Moritz的回答(0票)】:
这种说法首先是过于局限思维:说的是音乐,还是“用五线谱记录单音组合的单纯旋律性段落”?
首先要知道一点,旋律只是音乐的一个元素。
再就是,其实很多音乐是无法用乐谱记录的,比如爵士乐,就是继承了非洲音乐中极度个人化、记谱不能的特点,一些演奏法因为其浓厚的个体特质而无法被重复
【徐航的回答(0票)】:
看楼上们的回答让我想起了无限分割的说法。然后联想到经典物理向量子物理的过渡。所以音乐也是吧?于看似毫无可能处,突然出现新的可能。所以俺的观点是:不会穷尽的。
【吴洋的回答(0票)】:
个人感觉,人类基因密码子那么少,都找不出相同的人,我们唱的歌肯定达不到每人一首不同的歌
【arios的回答(0票)】:
绝对不可能。
构成音乐(旋律)的两大基本要素是音高和时长,音符只是标准音高的标记方式,而音高和时长本身是无限的,并且在一段旋律中音高和时长都可以复用。理论上,仅仅两个音符就能制造无限的旋律。
更何况,除了音高和时长,还有音色和强度这两个无限元素。
想想小提琴的一根弦,而不是钢琴的88个键。
【GothicMoron的回答(0票)】:
不会。人类增长的脑容量与智力会使音乐的音符越来越多。即使用完了12平均率(其实用不完)也有更多其他音律可以被创造
知乎用户的回答(258票):
很难!一首歌曲是由歌 + 曲 + 演唱者, 三个元素组成。曲可能会重复或相似,但词 和 演唱者 却很难。 因为这两者通常带有时代烙印,而时代过去了的,就回不来了。
【李根的回答(0票)】:
我初中的时候问过我老师,他说用不完。我觉得音乐就是一种语言一种情绪的表达,有逻辑,有思想,你见过一个人说话太多变哑巴的吗。音乐又好像是油画,一个音符就是一个色块。颜色就七种,组合出来就是一部画作。音符是一滴水,存在于旋律的海洋。
【张海富的回答(0票)】:
你想一下,就是一台显示器,有若干个像素,像素的各种明暗组合,也是有限的,这个组合可以看到所有的图画,难道美术画图也是有限的吗?但是这个数字会达到比宇宙所有粒子数量还要多的数字,可以当成无穷来理解的。哈。
【PrestonM的回答(0票)】:
刘慈欣的小说《诗云》里面就是,外星人被中文古诗惊叹到了,于是打算穷尽所有汉字的组合来寻找好作品,于是把整个太阳系的原子都拿了去做存储介质。
音乐所用的音高要比中文要少,可是音乐是多维度,或者说无限维度的(从声部角度),所以这两问题很相近。
所以说,要穷尽还是可能的,只是可能投入也接近无穷……
知乎用户的回答(258票):
个人以为是可以穷尽的,但是会是一个非常大的数据,因为我们不可能创造无限长的音乐,所以我认为音乐的长度一定是有限的,在有限的长度中,只有有限的可能性,虽然大,但不代表无限。
【傅未未的回答(0票)】:
我從小就想過很多次這個問題,每次答案都會在yes和no之間反覆。。。。
【梁明霖的回答(0票)】:
见“博尔赫斯的图书馆”。理论上如果把文字的排序穷尽了,那么人类的未来和过去,未知与已知都将包括在这个图书馆里面。在这种样本里发现一个东西和创造一个东西的意义同等。因此在音符这个问题上,音符的组合因为长度没有被限制,那么它的组合是无穷的。而如果有长度限制,人们只需要不断在里面搜索悦耳的音乐就能成为音乐家了。但,采用创作的方式或许更有效率。
【张翔的回答(0票)】:
有一个关键问题,不确定长度的话,即使可用元素再少那么排列方式也是无穷的,因为整数是无穷的。
知乎用户的回答(258票):
我认为从数学上讨论这个问题意义不大.
即使所有的组合都被人写出来了,人们能记得几首?
古典作品数量那么多,我们听过的记得的有多少,即使专业研究音乐的又能熟悉多少,
古典时期的作曲家很多 ,只有那些大师被人记得,那些二三流作曲家的作品估计早进图书馆无人问津了.
如果现在写一首曲子有一段或一句不小心和历史上出现过的某首不出名的作品几乎一样,恐怕也没人发现
所以我觉得这个问题不用担心.
【李滢浩的回答(0票)】:
有限并不是无限。宇宙中基本粒子的数量大约10的70次方这么个数量级。不可能储存超过此数目的信息。也不可能穷尽超过此数量的可能。
知乎用户的回答(258票):
楼上已经说得很多了,我就给个链接让大家听听那些非常接近的旋律吧:
http://www.61k.com
http://www.61k.com2012/01/30/the-most-used-melody-in-pop-music/
下面这个链接里的旋律也被学友的《一千个伤心的理由》用过
【春冯化雨的回答(0票)】:
文章本天成,妙手偶得之
【包尔的回答(0票)】:
用数学的方法来解释音乐和艺术,甚至用上统计学,thats Ridiculous,恕我直言了
人们为了记忆和保存,只是用了音符等“工具”,音符这东西虽然只有12个,但是可以看成多维的,我们只是觉得有些旋律好像接近熟悉,是因为近代的一些音乐的“模式化”东西,控制了我们的思维模式,流行音乐的祖宗Blues,只是用了音阶里的最简单的组合,从而引发了现代音乐整体的爆炸。这就证明了音乐的力量,才仅仅被挖掘了冰山一角。我们也再等,如果有一种新鲜的音乐元素诞生和广发推广应用,才会带来音乐的又一次历史性的革命。(别跟我说电子乐 DJ哪些玩意~已经革命了)
音乐的爹,巴赫叔叔,已经像物理数学家一样,把音程的关系像乐高积木一样来回来去的排列组合,这几百年在无人敢于说突破的对音乐在这些序列上的理解。我们现在只是掰了一支树杈挥舞着高兴,而这棵巨树枝繁叶茂,我等凡夫俗子哪有耐心仔细欣赏每一片叶脉中的品味和凳次!
以上拙见~
【陈善上的回答(1票)】:
这个问题,刘慈欣的小说《吞噬者》《诗云》可以回答你。
【宋健的回答(5票)】:
早在20世纪初你的这个想法就被音乐家们实践了!结果是很多科学家成了作曲家!了解一下20世纪音乐时期,你就会有所感触!比如,勋伯格创立的十二音体系,他早年创作的了几部传统作品,结果被评论家说像这个像那个的,他就有点不高兴,他就像能不能弄出个音乐来跟他们的都不一样,甚至他提出现在所有人创作的音乐都是以前作曲家创作音乐的复制品。
个人认为:音乐是非推理性符号学,就别用理性的东西去衡量它。让大家接受才是正道!
【赵跃的回答(0票)】:
排列组合的问题 数学老师告诉我们说 会有这样的一天 如果真的有人能活那么久的话
【明泰雷的回答(0票)】:
这样也可以的话,五言绝句会先很多步写完,这样的想法可以看大刘的一片小说《诗云》。
【李鹏的回答(2票)】:
IPV4用完了不是还有IPV6吗
【解磊的回答(3票)】:
直接给答案,绝对不会。
有这种想法,完全是因为你将音乐“机械化”了,“音符的排列组合”也许有一天的真的可以被穷举完,但音乐不能,因为“音符的排列组合”远远不等同于“乐曲”!
首先,乐谱不仅仅是那些蝌蚪状音符,还有那些小节线、休止符、谱号等等太多其他部分的组合,这些在一起,才算的上一份“完整的乐谱”,但也仅是乐谱而已,离“音乐”还差得远。
然后呢,音乐是需要演绎的!你见过谁翻翻乐谱YY一下就陶醉在音乐的旋律里了吗?同样的乐谱,用钢琴、小提琴、人声等来演绎,那是完完全全不一样的感觉,完完全全不一样的音乐,这个,你靠啥穷举?
再然后,音乐要靠人来演绎。为什么有人听音乐会计较版本?那是因为就算同一首曲子,一个人不同时期的演绎也会有所差异。且不提交响乐这样节奏复杂的音乐作品,哪怕是钢琴奏鸣曲这样单一乐器的独奏音乐,一个人一生中不同时期的演奏,也足以让你听出明显的不同。
最后,是我回答所有音乐类问题都会提到的,音乐是主观的,是有情绪色彩的。哪怕前面所说的所有变量全都控制住,你和我听同一首乐曲的体验也是不同的,你听到秋意正浓,我听到淡淡的哀愁,而这些情绪体验,才是音乐带给你的最核心、最珍贵的东西。
总结一下,音乐绝不可能被穷举,是因为音乐绝不仅仅是“音符的排列组合”;因为我们是有血有肉的人,而不是冷冰冰的机械。
另附一个相关问题的回答:一首鋼琴曲由人演奏和由電腦合成有什麼區別?有可能沒有區別嗎?如果是人聲呢?
最最后,引用卓别林《大独裁者》中的一句话:We think too much and feel too little!
【Anonymous的回答(1票)】:
假设一首歌三分钟,每秒唱一个音符,每个音符有十种选择则备选方案有10^180
假设地球上曾经存在过1000亿人也就是10^12,
则每个在地球上存在过的人需要创作10^168首曲子,才能被用完
假设每个人创作100首曲子,则需要10^178个人
到目前地球存在过的人的总数也不超过10^12个
所以几乎没有可能
原文地址:知乎
三 : 排列组合公式
排列组合公式
1.分类计数原理(加法原理)
N?m1?m2???mn.
2.分步计数原理(乘法原理)
N?m1?m2???mn.
3.排列数公式
n!
mAn!=n(n?1)?(n?m?1)=(n?m).(n,m∈N*,且m?n). 注:规定0!?1.
4.排列恒等式
mm?1A?(n?m?1)Ann(1); (2)mAn?nmAn?1n?m;
mm?1A?nAnn?1; (3)
nn?1nnA?A?Ann?1n(4);
mmm?1A?A?mAn?1nn(5).
(6) 1!?2?2!?3?3!???n?n!?(n?1)!?1.
5.组合数公式
Anmn(n?1)?(n?m?1)n!mmCnA?(n?m)!1?2???mm===m!(n∈N*,m?N,且m?n).
6.组合数的两个性质
mn?mCCnn(1)= ;
mm?1mCCCnnn(2) +=?1.
0C?1. n注:规定
7.组合恒等式 mCn?
(1)n?m?1m?1Cnm;
(2)mCn?nmCn?1n?m; nm?1Cn?1m;
r
n(3)mCn?
(4)r?0?Cn=2; n
rrrrr?1C?C?C???C?Crr?1r?2nn?1. (5)
012rnnC?C?C???C???C?2nnnnn(6).
135024n?1C?C?C???C?C?C??2nnnnnn(7).
123nn?1C?2C?3C???nC?n2nnnn(8).
r0r?110rrrCC?CC???CC?Cmnmnmnm?n. (9)
021222n2n(C)?(C)?(C)???(C)?Cnnn2n. (10)n
8.排列数与组合数的关系
mmAn?m!?Cn .
9.单条件排列
以下各条的大前提是从n个元素中取m个元素的排列.
(1)“在位”与“不在位”
m?1An①某(特)元必在某位有?1种;
mm?11m?1A?A?AAnn?1n?1n?1(着眼位置)②某(特)元不在某位有(补集思想)
m1m?1?An?AA?1m?1n?1(着眼元素)种.
(2)紧贴与插空(即相邻与不相邻)
AA①定位紧贴:k(k?m?n)个元在固定位的排列有kn?k种.
AA②浮动紧贴:n个元素的全排列把k个元排在一起的排法有n?k?1k种.
注:此类问题常用捆绑法;
③插空:两组元素分别有k、h个(k?h?1),把它们合在一起来作全排列,k个的
hkAAh?1种. h一组互不能挨近的所有排列数有n?k?1kkm?k
(3)两组元素各相同的插空
m个大球n个小球排成一列,小球必分开,问有多少种排法?
nAmn?1
?Cm?1nAn?m?1n?m?1当时,无解;当时,有n种排法.
n
Cm(4)两组相同元素的排列:两组元素有m个和n个,各组元素分别相同的排列数为?n.
10.分配问题
(1)(平均分组有归属问题)将相异的m、n个物件等分给m个人,各得n件,其分配方
nnnnn
N?Cmn?Cmn?n?Cmn?2n???C2n?Cn?
法数共有
(mn)!
(n!)m.
(2)(平均分组无归属问题)将相异的m·n个物体等分为无记号或无顺序的m堆,其
分配方法数共有
nnnnnCmn?Cmn?C...?C?C(mn)!?nmn?2n2nn
N??
m!m!(n!)m.
(3)(非平均分组有归属问题)将相异的
须被分完,分别得到
P(P=n1+n2+?+nm)个物体分给m个人,
物件必
n1,n2,…,nm件,且n1,n2,…,nm这m个数彼此不相
nmn1n2
N?Cp?CpCn?m!??n1...m
等,则其分配方法数共有
p!m!
n1!n2!...nm!.
(4)(非完全平均分组有归属问题)将相异的
件必须被分完,分别得到
P(P=n1+n2+?+nm)个物体分给m个人,物
n1,n2,…,nm件,且n1,n2,…,nm这m个数中分别
N?
nmn1n2
Cp?CpCn?m!?n1...m
有a、b、c、…个相等,则其分配方法数有
a!b!c!...
?
p!m!
n1!n2!...nm!(a!b!c!...).
(5)(非平均分组无归属问题)将相异的
P(P=n?+n1+n2+m)个物体分为任意的n1,
n2,…,nm件无记号的m堆,且n1,n2,…,nm这m个数彼此不相等,则其分
N?
配方法数有
p!
n1!n2!...nm!.
(6)(非完全平均分组无归属问题)将相异的
P(P=n1+n2+?+nm)个物体分为任意的n1,
n2,…,nm件无记号的m堆,且n1,n2,…,nm这m个数中分别有a、b、c、…
N?
个相等,则其分配方法数有
p!
n1!n2!...nm!(a!b!c!...).
p?n1+n2+?+nm)
(7)(限定分组有归属问题)将相异的p(个物体分给甲、乙、丙,……
等m个人,物体必须被分完,如果指定甲得则无论
n1件,乙得n2件,丙得n3件,…时,
n1,n2,…,nm等m个数是否全相异或不全相异其分配方法数恒有
p!
n1!n2!...nm!.
nmn1n2
N?Cp?CpCn??n1...m
11.“错位问题”及其推广
贝努利装错笺问题:信n封信与n个信封全部错位的组合数为
f(n)?n![
1111?????(?1)n]2!3!4!n!.
推广: n个元素与n个位置,其中至少有m个元素错位的不同组合总数为
1234
f(n,m)?n!?Cm(n?1)!?Cm(n?2)!?Cm(n?3)!?Cm(n?4)!
pm
???(?1)pCm(n?p)!???(?1)mCm(n?m)!
1234pmCmCmCmCmpCmmCm
?n![1?1?2?2?4???(?1)p???(?1)m]
AnAnAnAnAnAn.
12.不定方程
x1+x2+?+xn?m的解的个数
n?1
?
Cx+x+?+x?mn,m?N12n(1)方程()的正整数解有m?1个.
1?
Cnn??x+x+?+x?mn,m?N12nm?1个. (2) 方程()的非负整数解有
?
x+x+?+x?mx?k(k?N?,2?i?n?1)的非负n,m?N12n(3) 方程()满足条件i
整数解有
n?1
Cm
?1?(n?2)(k?1)
个.
?
x+x+?+x?mx?k(k?N?,2?i?n?1)的正整n,m?N12n(4) 方程()满足条件i
数解有
11n?12n?1n?2n?2n?1
Cnn???CC?CC???(?1)Cn?2Cm?1?(n?2)k
m?1n?2m?n?k?2n?2m?n?2k?3
个.
n0n1n?12n?22rn?rrnn(a?b)?Ca?Cab?Cab???Cab???Cnnnnnb ; 13.二项式定理
二项展开式的通项公式
rn?rr
Tr?1?Cnab(r?0,1,2?,n).
四 : excel利用排列组合公式列出所有排列组合情况
[排列组合公式]excel利用排列组合公式列出所有排列组合情况——简介本例主要介绍如何在Excel中把两组数据的组合全部列出来。
 [排列组合公式]excel利用排列组合公式列出所有排列组合情况——知识点
[排列组合公式]excel利用排列组合公式列出所有排列组合情况——知识点Excel
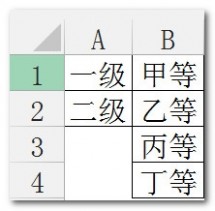
[排列组合公式]excel利用排列组合公式列出所有排列组合情况——操作过程:[排列组合公式]excel利用排列组合公式列出所有排列组合情况 一首先,看一下原始数据。A1和A2是两个主等级,B1:B4是四个附属等级,每个主等级都有四个附属等级。需要在C列显示出所有的组合情况。
 [排列组合公式]excel利用排列组合公式列出所有排列组合情况 二
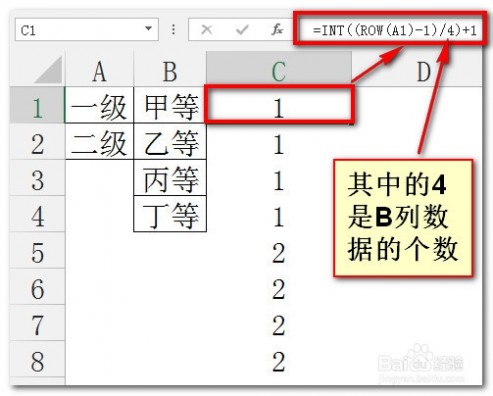
[排列组合公式]excel利用排列组合公式列出所有排列组合情况 二我们考虑用INDEX函数来实现这个功能。首先来看一下INDEX第二参数如何做。
双击C1,输入公式=INT((ROW(A1)-1)/4)+1,下拉可以看到1出现了4次,2也出现了4次,这是因为B列数据4次以后就需要在A列偏移一个单元格。
 [排列组合公式]excel利用排列组合公式列出所有排列组合情况 三
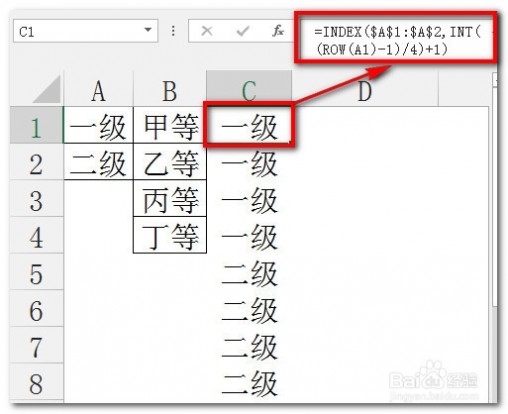
[排列组合公式]excel利用排列组合公式列出所有排列组合情况 三外面嵌套INDEX函数,输入:
=INDEX($A$1:$A$2,INT((ROW(A1)-1)/4)+1)
下拉后就可以看到“一等”和“二等”各出现了4次。
 [排列组合公式]excel利用排列组合公式列出所有排列组合情况 四
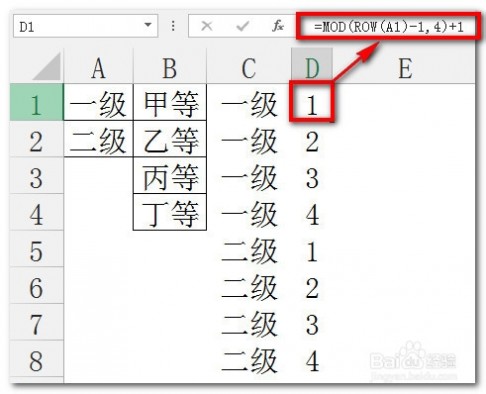
[排列组合公式]excel利用排列组合公式列出所有排列组合情况 四第二列数据和第一列数据不一样,我们需要循环引用B列的数据。也就是让1,2,3,4循环出现。所以我们考虑用MOD函数。双击D1,输入公式:
=MOD(ROW(A1)-1,4)+1
下拉后我们可以看到如下图的效果:
 [排列组合公式]excel利用排列组合公式列出所有排列组合情况 五
[排列组合公式]excel利用排列组合公式列出所有排列组合情况 五同样,外层嵌套INDEX函数,可以循环获得B列的数据,4行一遍:
=INDEX($B$1:$B$4,MOD(ROW(A1)-1,4)+1)
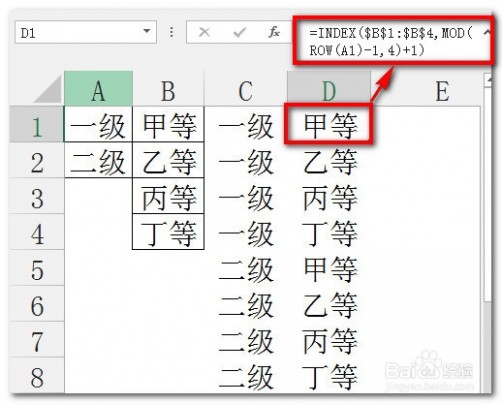 [排列组合公式]excel利用排列组合公式列出所有排列组合情况 六
[排列组合公式]excel利用排列组合公式列出所有排列组合情况 六最后,我们把公式合并在一个单元格中,就生成了最终结果组合。
=INDEX($A$1:$A$2,INT((ROW(A1)-1)/4)+1)&INDEX($B$1:$B$4,MOD(ROW(A1)-1,4)+1)
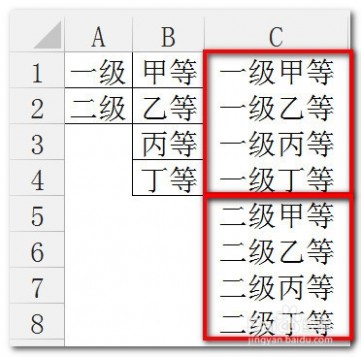 [排列组合公式]excel利用排列组合公式列出所有排列组合情况——注意事项
[排列组合公式]excel利用排列组合公式列出所有排列组合情况——注意事项如果您觉得此经验有用,可以点击本页面右上方的【大拇指】图案和【收藏按钮】或者右下方的【分享】按钮,也可以点击本注意事项下方的【收藏】按钮。
如需要了解更多内容,可以百度搜索“百度经验shaowu459”或到百度知道向我提问。
本文标题:
排列组合公式-排列组合的求和公式 本文地址:
http://www.61k.com/1124977.html 

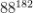
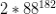
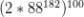


 [排列组合公式]excel利用排列组合公式列出所有排列组合情况——知识点
[排列组合公式]excel利用排列组合公式列出所有排列组合情况——知识点




 [排列组合公式]excel利用排列组合公式列出所有排列组合情况——注意事项
[排列组合公式]excel利用排列组合公式列出所有排列组合情况——注意事项