一 : 某工程队修一条公路己修了1200米这时己修和未修的长度比是4:3

某工程队修一条公路己修了1200米这时己修和未修的长度比是4:3

某工程队修一条公路己修了1200米这时己修和未修的长度比是4:3的参考答案

某工程队修一条公路己修了1200米这时己修和未修的长度比是4:3,这条路长多少米?

1200×3/4+1200

=900+1200

=2100米

二 : 用方程解决实际问题（1）某工程队承接了3000米的修路任务，在修好600米后，引进了新设备，工作效率

用方程解决实际问题 （1）某工程队承接了3000米的修路任务，在修好600米后，引进了新设备，工作效率是原来的2倍，一共用30天完成了任务，求引进新设备前平均每天修路多少米？ （2）某工厂计划生产A，B两种产品共10件，其生产成本和利润如下表： A种产品 B种产品 成本（万元∕件） 3 5 利润（万元∕件） 1 2 ①若工厂计划获利14万元，问A，B两种产品应分别生产多少件？ ②若工厂投入资金不多于44万元，且获利多于14万元，问工厂有哪几种生产方案？ ③在②条件下，哪种方案获利最大？并求最大利润．

题型：解答题难度：中档来源：不详

（1）设引进新设备前平均每天修路x米． 根据题意，得： 600 x + 3000-600 2x =30． 解得：x=60． 经检验：x=60是原方程的解，且符合题意． 答：引进新设备前平均每天修路60米． （2）①设A种产品x件，B种为（10-x）件， x+2（10-x）=14， 解得x=6， A生产6件，B生产4件； ②设A种产品x件，B种为（10-x）件， 3x+5(10-x)≤44 x+2(10-x)＞14 ， 解得：3≤x＜6． 方案一：A生产3件 B生产7件； 方案二：A生产4件，B生产6件； 方案三：A生产5件，B生产5件． ③第一种方案获利最大． 设A种产品x件，所获利润为y万元， ∴y=x+2（10-x）=-x+20， ∵k=-1＜0， ∴y随x的增大而减小， ∴当x=3时，获利最大， ∴3×1+7×2=17， 最大利润是17万元．

考点：

考点名称：一元一次不等式组的应用应用：列一元一次不等式组解决实际问题。

一元一次不等式的应用主要涉及问题：
1.分配问题：
例：一堆玩具分给若干个小朋友，若每人分3件，则剩余4件，若前面每人分4件，则最后一人得到的玩具最多3件，问小朋友的人数至少有多少人？。

2.积分问题：
例：某次数学测验共20道题（满分100分）。评分办法是：答对1道给5分，答错1道扣2分，不答不给分。某学生有1道未答。那么他至少答对几道题才能及格？

3.比较问题:
例：某校校长暑假将带领该校“三好学生”去三峡旅游，甲旅行社说：如果校长买全票一张，则其余学生可享受半价优惠；乙旅行社说：包括校长在内全部按全票的6折优惠。已知两家旅行社的全票价都是240元，至少要多少名学生选甲旅行社比较好？

4.行程问题:
例：抗洪抢险，向险段运送物资，共有120公里原路程，需要1小时送到，前半小时已经走了50公里后，后半小时速度多大才能保证及时送到？

5.车费问题:
例：出租汽车起价是10元(即行驶路程在5km以内需付10元车费),达到或超过5km后,每增加1km加价1.2元(不足1km部分按1km计),现在某人乘这种出租 汽车从甲地到乙地支付车费17.2元,从甲地到乙地的路程超过多少km?

6.浓度问题:
例：在1千克含有40克食盐的海水中，在加入食盐，使他成为浓度不底于20%的食盐水，问：至少加入多少食盐？

7.增减问题:
例：一根长20cm的弹簧，一端固定，另一端挂物体。在弹簧伸长后的长度不超过30cm的限度内，每挂1㎏质量的物体，弹簧伸长0.5cm.求弹簧所挂物体的最大质量是多少？

8.销售问题:
例：商场购进某种商品m件，每件按进价加价30元售出全部商品的65%，然后再降价10%，这样每件仍可获利18元，又售出全部商品的25%。
(1)试求该商品的进价和第一次的售价；
(2)为了确保这批商品总的利润率不低于25%，剩余商品的售价应不低于多少元？

一元一次不等式组解应用题的一般步骤为：
列不等式组解决实际问题的步骤与列一元一次不等式解应用题的步骤相类似,所不同的是,前者需寻求的不等关系往往不止一个,而后者只需找出一个不等关系即可。
（1）审：认真审题，分清已知量、未知量及其关系，找出题中的不等关系，要抓住题中的关键词语，如“大于”、“小于”、“不大于”、“至少”、“不超过”、“超过”等；
（2）设：设出适当的未知数；
（3）列：根据题中的不等关系列出不等式组；
（4）解：解出所列不等式组的解集；
（5）答：写出答案，从不等式组的解集中找出符合题意的答案，并检验是否符合题意。考点名称：分式方程的应用

列分式方程解应用题和列整式方程解应用题步骤基本相同，但必须注意，要检验求得的解是否为原方程的根，以及是否符合题意。
列分式方程解应用题的一般步骤是：
①找等量关系（审）:理解题意,弄清具体情境中的已知量与未知量以及它们之间的基本关系;
②设:设未知数,用含x（或其他字母）表示某个未知数，由该未知数与其他数量的关系，写出表示相关量的式子；
③列：找出相等关系，列出分式方程；
④解：解这个分式方程；
⑤检验：双重检验，先检验是否为增根，再检验是否符合题意；
⑥答：写出答案。

例题
南宁到昆明西站的路程为828KM，一列普通列车和一列直达快车都从南宁开往昆明。直达快车的速度是普通快车速度的1.5倍,普通快车出发2H后，直达快车出发,结果比普通列车先到4H,求两次的速度.
设普通车速度是x千米每小时则直达车是1.5x
由题意得：
828/x-828/1.5x=6 ，
(828×1.5-828)/1.5x=6 ，
414/1.5=6x，
x=46, 1.5x=69
答：普通车速度是46千米每小时，直达车是69千米每小时。

无解的含义：
1.解为增根。
2.整式方程无解。（如：0x不等于0.）

用分式解应用题的常见题型：
（1）行程问题有路程、时间和速度三个量，其关系式是路程=速度×时间，一般式以时间为等量关系。
（2）工程问题有工作效率、工作时间和工作总量三个量，其关系式是工作总量=工作效率×工作时间。
（3）增长率问题，其等量关系式是原量×（1+增长率）=增长后的量，原量×（1+减少率）=减少后的量。

三 : 汛期来临前，滨海区决定实施“海堤加固”工程，某工程队承包了该项日，计划每天加固60米.在施工前，得到

汛期来临前，滨海区决定实施“海堤加固”工程，某工程队承包了该项日，计划每天加固60米. 在施工前，得到气象部门的预报，近期有“台风”袭击滨海区. 于是工程队改变计划，每天加固的海堤长度是原计划的1.5倍. 这样赶在“台风”来临前完成加固任务. 设滨海区要加固的海堤长为a米，则完成整个任务的实际时间比原计划时间少用了( )天(用含a 的代数式表示).

题型：填空题难度：中档来源：同步题

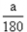考点：

考点名称：写代数式代数式：
由数和表示数的字母经有限次加、减、乘、除、乘方和开方等代数运算所得的式子，或含有字母的数学表达式称为代数式。
数的一切运算规律也适用于代数式。单独的一个数或者一个字母也是代数式。
例如：ax+2b，－2/3，b^2/26，√a+√2等。
带有“(≥)” “=”“≠”等符号的不是代数式
注意：
1、不包括等于号（=、≡）、不等号（≠、≤、≥、<、>、≮、≯）、约等号≈。
2、可以有绝对值。例如：|x|，|-2.25| 等。代数式的书写要求：
一、数字与数字相乘时，中间的乘号不能用“? ”代替，更不能省略不写。
如：4乘5，写作4×5，不能写成4?5，更不能写成45
二、数字与字母相乘时，中间的乘号可以省略不写，并且数字放在字母的前面。
如： a的5倍，写作：5a不要写成a5。
三、两个字母相乘时，中间的乘号可以省略不写，字母无顺序性
如： a乘b ，写成ab或ba
四、当字母和带分数相乘时，要把带分数化成假分数。
如：3 1/2 乘a 写作：7/2 a 不要写成32/1a
五、含有字母的除法运算中，最后结果要写成分数形式，分数线相当于除号。
如：5除以a 写作5/a ， 不要写成5÷a ； c除以 d写作 ，不要写成 c÷ d
六、如果代数式后面带有单位名称，是乘除运算结果的直接将单位名称写在代数式后面，若代数式是带加减运算且须注明单位的，要把代数式括起来，后面注明单位。
如：甲同学买了5本书，乙同学买了a 本书，他们一共买了（5+a ）本。

代数式的书写格式：
（1）数与字母，字母与字母相乘，乘号可以省略，也可写成“.”；
（2）数字要写在前面；
（3）带分数一定要写成假分数；
（4）在含有字母的除法中，一般不用“÷”号，而写成分数的形式；
（5）式子后面有单位时，和差形式的代数式要在单位前把代数式括起来。

代数式：

四 : 某工程队承包某标段全长1755米

某工程队承包某标段全长1755米

某工程队承包某标段全长1755米的参考答案

（1）设乙每天掘进x米,甲就是x+0.6米

所以

（x+x+0.6）×5=45

10x+3=45

10x=42

x=4.2

x+0.6=4.8米

答：乙掘进4.2米,甲掘进4.8米

（2）

甲组就是4.8+0.2=5米,乙组就是：4.2+0.3=4.5米

设比原来少用x天

所以

（1755-45）÷（5+4.5）=（1755-45）÷（4.2+4.8）-x

1710÷9.5=1710÷9-x

180=190-x

x=10

答：少用10天

五 : 某工程队承包了一段高速公路建设任务.开工十五个月已完成的工程量与工程总量的比是3:5，如果再修建

比比读小说网比比读小说网”，不装app也能追书！

本文标题：某工程队承包了-某工程队修一条公路己修了1200米这时己修和未修的长度比是4:3
本文地址： http://www.61k.com/1120563.html