一 : 板式塔流体力学特性的测定

化工基础实验报告

实验名称板式塔流体力学特性的测定

班级姓名学号成绩

实验时间同组成员

一、实验目的

1、观察塔板上气液两相流动状况，测量气体通过塔板的压力降与空塔气速的关系；测定雾沫夹带量、漏液量与气速的关系；

2、研究板式塔负荷性能图的影响因素，作出筛孔塔板或斜孔塔板的负荷性能图；比较筛孔塔板与斜孔塔板的性能；

二、实验原理

板式塔流体力学特性测定

塔靠自下而上的气体和自上而下的液体逆流流动时相互接触达到传质目的，因此，塔板传质性能的好坏很大程度上取决于塔板上的流体力学状态。［www.61k.com）当液体流量一定，气体空塔速度从小到大变动时，可以观察到几种正常的操作状态：鼓泡态、泡沫态和喷射态。当塔板在很低的气速下操作时，会出现漏液现象；在很高的气速下操作，又会产生过量液沫夹带；在气速和液相负荷均过大时还会产生液泛等几种不正常的操作状态。塔板的气液正常操作区通常以塔板的负荷性能图表示。负荷性能图以气体体积流量（m3/s）为纵坐标，液体体积流量（m3/s）为横坐标标绘而成，它由漏液线、液沫夹带线、液相负荷下限线、液相负荷上限线和液泛线五条线组成。当塔板的类型、结构尺寸以及待分离的物系确定后，负荷性能图可通过实验确定。

传质效率高、处理量大、压力降低、操作弹性大以及结构简单、加工维修方便是评价塔板性能的主要指标。为了适应不同的要求，开发了多种新型塔板。本实验装置安装的塔板可以更换，有筛板、浮阀、斜孔塔板可供实验时选用，也可将自行构思设计的塔板安装在塔上进行研究。

筛板的流体力学模型如下：

1) 压降

?p??pc??pl

式中，Δp—塔板总压降，Δpc—干板压降，Δpl—板上液层高度压降，

其中 ?pc?0.051?vg(u02) c0

式中ρv—气相密度，kg/m3；g—重力加速度，m/s2，u0—筛孔气速，m/s，c0—筛孔流量系数，

筛板上因液层高度产生的压降Δpl即液层有效阻力hl：

?pl??lghl 式中ρl—液相密度，kg/m3，g—重力加速度,m/s2，hl—液层有效阻力，m液柱。

2) 漏液

板式塔 板式塔流体力学特性的测定

为保证筛孔不漏液的下限气速为u0m，筛板的u0m可按下面的经验式进行计算：

uom?4.4c0(0.0056?0.13hl?h?)?l?v

式中，u0m—漏液点的筛孔气速，m/s；hL—板上清液层高；hL?hw＋how，m；

hσ—与液体表面张力相当的液柱高度，m液柱。（www.61k.com)

h??4? 9810?l.d0

其中：σ—液体表面张力，N/m；ρl—液体密度，kg/m3；d0—筛孔孔径，mm

3) 过量液沫夹带

ev?5.7?10?6

?(uG)3.2 HT?hf

式中：ev—液沫夹带量，kg液/kg气；σ—液相表面张力，N/m；

uG—按有效截面积计算的气速； uG?

—塔截面积，m2；Af—降液管截面积，m2；

HT—板间距，m；

hf—鼓泡层高度，hf?Vs，m/s；Vs—气相负荷，m3/s；ATAT?AfhL，hL—板上清液层高度，m；Φ—鼓泡层平均相对密度，?

一般情况下，取Φ=0.4，即hf=2.5hL。

斜孔塔板的流体力学模型

斜孔塔板一排排的斜孔与液流方向垂直，气体从斜孔水平喷出，相邻两排孔口方向相反，交错排列，起到相互牵制的作用。既有气流水平喷出的优点，又消除了气流对撞转为向上冲的现象，板上保证均匀的低液面，使得气体和液体不断分散和聚集，通量比普通筛板可增大30％～40％。

斜孔塔板属筛板型塔板，其设计及计算方法与筛板塔类似。由于其结构上的特点，在阻力降、漏液和夹带的计算公式上与筛板又有不同。

1) 压降

干板压降可按下式计算：

2u0?pc??.?v 2

式中：Δpc—干板压降，ζ—干板阻力系数，实验测定ζ=2.1；

液层压降可按下式计算：

hl??.?lghL???lg(hw?how)

式中：hl—液层压降，Pa；ε—发泡系数，对于水—空气系统，ε=0.5

hw—堰高；how—堰上液头高；

2) 漏液

板式塔 板式塔流体力学特性的测定

为防止严重漏液，保证正常操作，斜孔塔板的孔动能因数F0必须满足下式： F0?8l

1000 式中：F0?u0v，ρl、ρv—液相、气相密度，kg/m3；u0—孔速，m/s；

3) 雾沫夹带

斜喷型塔板的雾沫夹带量均大大小于普通筛板的雾沫夹带值，但雾沫夹带的规律相似，斜孔塔板雾沫夹带计算公式如下：

ev?0.157(ug

HT?Hf)1.9(ev)0.7?0.2 ?l??v

式中：ev—雾沫夹带量，kg(液)/kg(气)；

ug—液层上部的气体流速，m/s；uG?Vs，m/s；Vs—气相负荷，m3/s；AT—AT?Af

塔截面积，m2；Af—降液管截面积，m2；ρl、ρv—液相、气相密度，kg/m3；

σ—液体表面张力，N/m；HT—板间距，m；

Hf—鼓泡层高度，Hf?F0hL，m；F0—孔动能因子，无因次；hL—板上清液层高5.3

度，m；

三、实验装置与流程

装置中的有关尺寸：

筛板塔

塔径D＝190mm 板间距HT＝294mm 堰高hW＝30mm

降液管底距塔板hO＝16mm 堰长LW＝130mm

孔径dO＝8mm 开孔数n＝36个 孔心距t＝21.5mm

开孔率：按传质区计算Ф＝12.6%，按塔截面积计算Ф＝6.38%

板式塔 板式塔流体力学特性的测定

图1 板式塔流体力学实验流程

1、水箱 2、离心泵 3、液体流量计 4、压差计 5、测量雾沫夹带 6、测量漏液 7、测量板上清液层高度

8、板式塔 9、气体流量计 10、漩涡气泵

四、操作注意事项

塔设备实验：

1． 不得急速开关阀门，以防损坏设备。（www.61k.com)

2． 不要让衣物、长发、饰品等接近风机吸入口；

3． 打开风机、水泵时务必保证出口阀门关闭，以防打坏转子流量计；

4． 进行实验操作时不要超过设备正常操作范围，以防设备损坏、大量水飞溅。

5． 先测定干塔、干填料压降与空塔速度的关系，不要开水泵以免淋湿塔板、填料。

6． 注意开关水泵、风机的顺序，防止水倒灌入气路。

五、实验原始数据表格：

1）设备参数

塔内径D＝190mm；

堰长lw?84mm；堰高hw?15mm；堰宽wd?27mm；

孔径d0?8mm；孔数n=36；t=20mm；开孔率??12.6%。

2）原始数据记录表

板式塔 板式塔流体力学特性的测定

六、数据处理

1．对原始数据表格中的数据进行换算

塔内径D＝190mm,则塔截面积A= 0.028m2；

板式塔 板式塔流体力学特性的测定

气速（m/s）=气体流量(m3/h)÷截面积（m2）÷3600=气体流量(m3/h)÷100.8 压降(pa)=压差计右（Pa）-压差计左（Pa） 漏液量（ml/S）=漏液量（ml）÷时间（S）

（1）喷淋密度830L/h下压降与气速的关系

板式塔 板式塔流体力学特性的测定

（2）喷淋密度1230L/h下压降与气速的关系

)

（3）不同喷淋密度下漏液量与气速的关系

板式塔 板式塔流体力学特性的测定

（3）不同喷淋密度下夹带量与气速的关系

4.气速从小到大塔板上的几种流动状态

实验时观察到了以下几种状态：漏液、鼓泡、泡沫。［www.61k.com]理论上，随着气速的继续增加，还会出现喷射态，但实验时未观察到。

漏液：气速很低时，液体从直接从筛孔中流下；

鼓泡：气速较低时气体以鼓泡形式通过液层；

板式塔 板式塔流体力学特性的测定

泡沫：气速增加，形成了在液体中大小不同尺寸的气泡的不规则运动及强烈的液体环流； 喷射：气速继续增加，而液体成为分散相，气体成为连续相。（www.61k.com）

七．思考题

1）从结构上分析斜孔塔板有何特点？它对塔的气体通量、板效率、阻力降有何影响？答：斜孔的方向与液流方向垂直，气体从孔中水平喷出，相邻两孔的孔口方向相反，交错排列，造成气、液高度湍流。防止了垂直上喷，减少雾沫夹带，有利于提高气体通量。同时该设计保证了板上均匀的低液面，使得气体和液体不断分散和聚集，板上的传质效率提高。同时，低液面也使得板上的压降大大降低。

2）定性分析液泛与哪些因素有关

答：当塔板上液体流量很大，上升气体的速度很高时，液体被气体夹带到上一层塔板上的量猛增，使塔板间充满了气、液混合物，最终使整个塔内都充满液体，这种现象称为夹带液泛。还有一种情况就是因降液管设计太小，流动阻力过大，液体不能正常地通过降液管向下流，使得液体在塔板上积累而充满整个板间，这种液泛成为溢流液泛。所以，液泛主要与气液两相的流量、以及降液管的设计等因素有关。

3）板间距加大，塔板的负荷性能图将发生什么变化？

答：板间距加大，使得液体更难被气体夹带到上一层塔板去，因此夹带线与液泛线上移。而由于液体在降液管中的停留时间不变，液相流量上限也会增加，所以液相流量上限线右移。

4）塔板上的流动状态主要取决于哪几个方面？

答：塔板上的流动状态主要受到塔板设备参数与操作条件两大方面的影响。设备参数如开孔的形式、孔径大小、降液管大小、塔板间距等；而操作条件如气、液流量等都将影响塔板上的流动状态。

二 : 流体力学重要公式

流体流动

流体特性→流体静力学→流体动力学 →流体的管内流动

gΔZ+Δu2/2+Δp/ρ=We-∑hf

静压能：p/ρ，J/kg

静压头：p/(ρg)，m

流体密度：ρ，kg/m3 ,不可压缩流体与可压缩流体

压强差：Δp， Pa, mmHg,表压强，绝对压强，大气压强，真空度流体静力学基本方程： gΔz+Δp/ρ=0

或 p1/ρ+gZ1=p1/ρ+gZ1

或 p=pA+hρg

应用：U型压差计

gΔZ+Δu2/2+Δp/ρ=We-∑hf

位能：gZ，J/kg

位头：Z，m

截面的选择

基准面的选定

gΔz+Δu2/2+Δp/ρ=We-∑hf

动能：u2/2，J/kg

动压头(速度头)： u2/(2g)，m

流速：u, m/s

当两截面积相差很大时，大截面上(贮液槽)u≈0

流体在圆管内连续定态流动：u2=u1(d1/d2)2

体积流速：qv, m3/s qv=uA

质量流速：qm, kg/s qm=qvρ=uAρ

流速测定：

变压差(定截面)流量计：测速管/孔板/文丘里 u=C(2Δp/ρ)1/2=C[2R(ρA-ρ)g/ρ]1/2

孔板C=0.6-0.7；测速管/文丘里C=0.98-1.0

变截面(定压差)流量计：转子流量计

gΔZ+Δu2/2+Δp/ρ=We-∑hf

管路总阻力： ∑hf=hf+hf’，J/kg；

总压头损失：Hf=∑hf/g，m

对静止流体或理想流体： ∑hf=0

直管阻力：hf=λ.L/d.u2/2

力学公式 流体力学重要公式

局部阻力：hf’=ζu2/2 (阻力系数法)或

hf’=λ.Le /d.u2/2 (当量长度法)

(进口：ζ=0.5；出口：ζ=1)

雷诺准数：Re=duρ/μ, 流型判断

管内层流：Re≤2000

ur=Δpf/(4μL).(R2-r2), u=umax/2；λ=64/Re 管内湍流：Re>2000

λ=0.3164/Re0.25 (光滑管)

λ=f(Re,ε/d)(粗糙管)

牛顿黏性定律：τ=μ(du/dy)

当量直径：de=4流通面积/润湿周边长度

gΔZ+Δu2/2+Δp/ρ=We-∑hf

有效功(净功)：We，J/kg；

有效压头：He=We/g，m

有效功率：Pe=Weqm,W

功率：P=Pe/η

非均相混合物分离及固体流态化

非均相混合物(颗粒相+连续相)→相对运动(沉降/过滤)→分离 颗粒相+连续相 →固体流态化→混合

沉降

沉降(球形颗粒)：

连续相：气体/液体

颗粒受力：（重力/离心）场力-浮力-阻力=ma

沉降速率

重力沉降 离心沉降

ζ=f(Ret,υs)，Ret=dutρ/μ<10-4-1(层流区),ζ=24/ Ret

离心分离因数

沉降设备设计

力学公式 流体力学重要公式

沉降条件： θ≥θt

重力沉降：降尘室 离心沉降：旋风分离器

生产能力

qv=blut qv=hBui

(qv与高度无关)

n层沉降室

qv=(n+1)blut

过滤（滤饼过滤）

恒压滤饼过滤

(忽略过滤介质阻力)

K过滤常数：K=2k(Δp)1-s, m2/s；

*K取决于物料特性与过滤压差;

单位过滤面积所得的滤液体积q=V/A，m3/m2；

单位过滤面积所得的当量滤液体积qe=Ve/A，m3/m2；

s-滤饼的压缩性指数

每得1m3滤液时的滤饼体积υ(1m3滤饼/1m3滤液)

体积为VW的洗水所需时间θW = VW/(dV/dθ)W

过滤机的生产能力(单位时间获得的滤液体积)

间歇式 连续式

Q=V/T=V/(θ+θW+θD)

若Ve可忽略

转筒表面浸没度 ψ=浸没角度/3600 转筒转速为 n-- r/min， 过滤时间 θ=60 ψ /n

传热

传热方式及定律

力学公式 流体力学重要公式

热传导：傅立叶定律

对流：牛顿冷却定律

辐射；斯蒂芬-波耳兹曼定律：Eb=σ0T4=C0(T/100)4

传热基本方程 Q=KS△tm

换热器的热负荷

用热焓

用等压比热容

用潜热

两平行灰体板间的辐射传热速度Q1-2

Q1-2=C1-2S[(T1/100)4-(T2/100)4

对流和辐射联合传热

总散热速率：Q=Qc+QR=αTSw(tw-tb)

αT=αc+αR

恒温传热 △tm=T-t

变温传热：平均温差

*逆流和并流

错流和折流 温差校正系数=f(P,R) 传热单元数法

计算确定Cmin→NTU,CR →ε →由冷热流体进口温度和ε →冷热出口温度

传热表面积

S=Q/(K△tm)

热传导和对流联合传热

总传热系数

力学公式 流体力学重要公式

Rso,Rsi垢阻； 壁阻

对流传热系数αi,αo

流体有相变时的对流传热系数

层流膜状冷凝时：努塞尔特方程 湍流液膜冷凝时：

水平管外液膜冷凝时：

液体沸腾传热系数：罗森奥公式：α=(Q/S)/Δt

蒸发

蒸发器的热负荷Q，kJ/h

Q=D(H-hc)=WH’+(F-W)h1-Fhc+QL

冷凝水在饱和温度下排出

Q=Dr=WH’+(F-W)h1-Fh0+QL

溶液稀释热可忽略

D=[Wr’ +Fc0(t1–t0)+QL]/r

r’=(H’-cWt1)近似可作为水在沸点t1的汽化热。［www.61k.com]

当原料液在沸点t1下加入(t0=t1),并忽略QL

D=Wr’/r

单位蒸气消耗量 e=D/W=r’/r

三 : 流体力学公式

第二章 流体的主要物理性质

? 流体的可压缩性计算、牛顿内摩擦定律的计算、粘度的三种表示方法。

1．密度 ρ = m /V

2．重度 γ = G /V

3．流体的密度和重度有以下的关系：γ = ρ g 或 ρ = γ/ g

4．密度的倒数称为比体积，以υ表示υ = 1/ ρ = V/m

5．流体的相对密度：d = γ流 /γ水 = ρ流 /ρ水

6．热膨胀性 ??1?V

V?T 1?V7．压缩性. 体积压缩率κ ???

8．体积模量 V?p

??V

9．流体层接触面上的内摩擦力 K?1?V?P

dn dv????10．单位面积上的内摩擦力（切应力）（牛顿内摩擦定律）

11．.动力粘度μ： ??

dnF??Ad??dv/dn

12．运动粘度ν ：ν = μ/ρ

13．恩氏粘度°E：°E = t 1 / t 2

第三章 流体静力学

? 重点：流体静压强特性、欧拉平衡微分方程式、等压面方程及其、流体静力学基本方程意义及其计算、

压强关系换算、相对静止状态流体的压强计算、流体静压力的计算（压力体）。

1．常见的质量力：

重力ΔW = Δmg、

直线运动惯性力ΔFI = Δm·a

离心惯性力ΔFR = Δm·rω2 .

2．质量力为F。：F = m ·am = m(fxi+fyj+fzk)

am = F/m = fxi+fyj+fzk为单位质量力，在数值上就等于加速度

实例：重力场中的流体只受到地球引力的作用，取z轴铅垂向上，xoy为水平面，则单位质量力在x 、y、 z轴上的分量为： fx= 0 , fy= 0 , fz= -mg/m = -g 式中负号表示重力加速度g与坐标轴z方向相反 3流体静压强不是矢量，而是标量，仅是坐标的连续函数。即：p= p(x,y,z)，由此得静压强的全微分为:

dp??x

4．欧拉平衡微分方程式

?pdx??p?ydy??p?zdzfxρdxdydz??p?x?p?y?p

?zdxdydz?0fyρdxdydz?dxdydz?0fzρdxdydz?dxdydz?0

1

单位质量流体的力平衡方程为：

1?p1?p1?pf??0f??0fy??0zx ρ?zρ?xρ?y

5．压强差公式（欧拉平衡微分方程式综合形式）

ρ(fxdx?fydy?fzdz)?dx?dy?dz ?x?y?z?p?p?p

6．质量力的势函数 dp?ρ(fxdx?fydy?fzdz)dp?ρ(fxdx?fydy?fzdz)??dU

?U?U?Udx?dy?dz=fxdx?fydy?fzdz7．重力场中平衡流体的质量力势函数 dU??x?y?z

??gdz积分得：U = -gz + c

8．等压 .面微分方程式 .fxdx + fydy + fzdz = 0

9．流体静力学基本方程

对于不可压缩流体，ρ = 常数。积分得

形式一：p + ?gz = c

pp形式二 1?gz1?2?gz2?c

形式三 z?p1?z?p2?c12ρgρg

10．压强基本公式p = p 0+? g h

11．.静压强的计量单位

? 应力单位：Pa、N/m2、bar

? 液柱高单位：mH2O、mmHg

? 标准大气压：1 atm = 760 mmHg =10.33 mH2O = 101325 Pa ≈ 1bar

第四章 流体运动学基础

1拉格朗日法：流体质点的运动速度的拉格朗日描述为

ρρ

压强 p的拉格朗日描述是：p=p(a,b,c,t)

2．欧拉法流速场 u?u(x,y,z,t)

?u?u(a,b,c,t)?????(a,b,c,t)?w?w(a,b,c,t)???????(x,y,z,t)?w?w(x,y,z,t)?????v?ui?vj?wk

压强场：p=p(x,y,z,t) ?????a?a(x,y,z,t)?axi?ayj?azk 2

加速度场 ?a?

?x

?

?

?ay?

?

简写为

dudtd?dt

??

du(x,y,z,t)

dtd?(x,y,z,t)

dt

??

?u?t???t

?u?u

?u?x???x

?υ??

?u?y???y

?w?w

?u?z???z

?dwdw(x,y,z,t)?w?w?w?w

???u???w?az?dtdt?t?x?y?z?

?t

??

(???)?时变加速度： 位变加速度

?t

3．流线微分方程：.在流线任意一点处取微小线段dl = dxi + dyj + dzk，

a?

??

?(???)?

该点速度为：v = ui + vj + wk，由于v 与dl 方向一致，所以有： dl× v = 0 4．流量计算：

单位时间内通过dA的微小流量为 dqv=udA 通过整个过流断面流量 qv??dqv??AudA相应的质量流量为

qm??qv?ρ?udA

A

5．平均流速：

6．连续性方程的基本形式

??

qvA

?

?

A

udAA

qv?vA

?ρ

?udA??udA??A111?V?tdV ?A222

?ρ

对于定常流动 ? 0 有 ? 1 ? A1 u 1 d A ? ? 2 ? A 2 u 2 d A 即?1A1?1= ?2A2?2

A 即A1?1=A2?2= qv 对于不可压缩流体，?1 = ?2 =c，有 ? u 1 d A ? ? u 2 d

???(?u)?(??)?(?w)

7．三元流动连续性方程式 ????0

?t?x?y?z

?(?u)?(??)?(?w)定常流动

A1

A2

?t

?x

?

?y

?

?z

?0

不可压缩流体定常或非定常流：? = c

8．雷诺数

?u?x

?

???y

?

?w?z

?0

Re?

?ud?

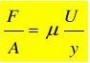
对于圆管内的流动：

Re<2000 时，流动总是层流型态，称为层流区； Re>4000时，一般出现湍流型态，称为湍流区；

2000<Re<4000 时，有时层流，有时湍流，处于不稳定状态，称为过渡区；取决于外界干扰条件。

9．牛顿黏性定律

10．剪切应力，或称内摩擦力， N/m2

????

duxdy

3

11．动力黏性系数

12．运动黏度 ? ? ?, m2/s

13．.临界雷诺数

?

le

14．进口段长度

d

第五章 流体动力学基础 1.欧拉运动微分方程式

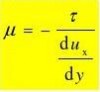
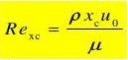
fx?

1?p

dudt

??x

?

fy?

1?p

??y

?

dvdt

fz?

1?p

??z

?

dwdt

2.欧拉平衡微分方程式 1?p1?pfx??0fy??0 ??x??y3.理想流体的运动微分方程式

fz?

1?p

??z

?0

1?p?u1?p?????????u?u?u

fy???u???wfx???u???w

??x?t??y?t?x?y?z?x?y?z

4.理想不可压缩流体重力作用下沿流线的伯努利方程式：三个式子

fz?

1?p

??z

?

?w?t

?u

?w?x

??

?w?y

?w

?w?z

?g?2

22

p1?1v1p2?2v2

??z2??5．理想流体总流的伯努利方程式 z1??g2g?g2g

2 p1V1p2

z1???1?z2???6．总流的伯努利方程

gz?

p

?

v

2

?c

z?

p

?g

?

v

2g

?c

z1?

p1

?

v1

2

2g

?z2?

p2

?g

?

v2

2

2g

?c

V2

2

2

g?2g

?

g?2g

2

7．实际流体总流的伯努利方程式

8．粘性流体的伯努利方程

9．.总流的动量方程

10．总流的动量矩方程

z1?

p1?1v1

2g

2

?g

?z2?

p2

?g

?

2

?2v2

2g

?hf

z1?

p1

?

?

v1

2

2g

?z2?

p2

?

?

v2

2g

?hL

?2?Q2V2??1?Q1V1?

?

?F

?

?2?Q2r2?V2??1?Q1r1?V1??r?F

M??Q(V2r2cos?2?V1r1cos?1)

4

功 W?

11．叶轮机械的欧拉方程

12．洒水器

?

?0

Md??M??M

d?dt

?M?

功率 P=

2?Q(VRcos???R)?0???

VRcos?

2

dWdt

第七章 流体在管路中的流动

d Vd1．临界雷诺数 V ? 临界雷诺数=2000，小于2000，流动为层流大于2000，流动为湍流

Re???

?

2．沿程水头损失 hf

?p1?p2?p

??

?当流动为层流时沿程水头损失hf为， V(1.0) ；

当流动为湍流时沿程水头损失hf为， V(1.75～2.0) 3．水力半径 ： r h ?A

P

相当直径 ：d h?4rh

4．圆管断面上的流量

Q?π4

8?

GR 15．平均流速 V ?QπR2

vmax

A?πR2?G2

18?R?2

vmax

6．局部阻力因数为 c?

?0f1 2?V

2

7．管道沿程摩阻因数 ??4c64

f?

Re

8．沿程水头损失的计算 ?64

22

hf?

?p

?

?

Gl

?

?

8?l

?R

2

V

l?Vd?d?V2g???lV

d?2g

第九章

?

1．.薄壁孔口特征：L/d≤2 厚壁孔口特征：2＜L/d≤4

12．流速系数 Cv?

??c

.3。流量系数 Cd = CcCv

5

四 : 工程流体力学相关概念公式 17

第二章 流体及其物理性质

流体：是一种受任何微小剪切力作用都能连续变形的物质。

流体连续介质假说：可以不去考虑分子间存在的空隙，而把流体视为由无数连续分布的流体微团所组成的连续介质。

作用在流体上的力：表面力和质量力。

流体密度：单位体积内所具有的质量。

压缩性：随着压强的增高，体积便缩小。压缩系数：用单位压强所引起的体积变化率。

膨胀性：随着温度的升高，体积便膨胀。体胀系数：单位温升所引起的体积变化率。

粘性：流体微团间发生相对滑移时产生切向阻力的性质。

牛顿内摩擦定律：作用在流层上的切向应力与速度梯度成正比，其比例系数为流体的动力粘度。

粘性与温度的关系：液体的粘度随温度上升而减小，气体的年度随温度上升而增大。

牛顿流体：凡作用在流体上的切向应力与它所引起的角变形速度（速度梯度）之间的关系符合牛顿内摩擦定律的流体。

第三章 流体静力学

流体静压强两个特性：一。流体静压强的方向沿作用面的内法线方向。

二。静止流体中任一点流体静压强的大小与其作用面在空

间的方位无关，只是该点坐标的连续函数，即静止流

体中任一点上不论来自何方的静压强均相等。

等压面：压强相等的各点组成的面。作用于静止流体中任一点的质量力必垂直于

通过该点的

等压面。

帕斯卡原理：施于在重力作用下不可压缩流体表面上的压强，将以同一数值沿各

个方向传递

到流体中的所有流体质点。

水头：单位重量流体所具有的能量用液柱高度表示。

压力体：液体作用在曲面上的总压力的铅直分力的大小恰好等于压力体的液体重

力，但并非

作用在曲面上的一定是它上面压力体的液体重力。（纯数学概念，与体内有无液

体无关）

第四章 流体运动学和流体动力学基础

流体运动的描述方法：欧拉方法和拉格朗日方法。

流线：在某一瞬时，一条曲线上的每一点的速度矢量总是在该点与此曲线相切。 流管：在流场内作一本身不是流线又不相交的封闭曲线，通过这样的封闭曲线上

各点的流线

所构成的管状表面。

有效截面：处处与流线相垂直的流束的截面。

湿周：在总流的有效截面上，流体同固体边界接触部分的周长。

水力半径：总流的有效面积与湿周之比。

第五章 相似原理和量纲分析

力学相似：包括几何相似、运动相似、动力相似。

弗劳德数Fr的物理意义：惯性力与重力的比值。

雷诺数Re的物理意义：惯性力与粘滞力的比值。

斯特劳哈尔Sr的物理意义：当地惯性力与迁移惯性力的比值。

第六章 管内流动和水力计算 液体出流

局部能量损失：发生在流动状态急剧变化的急变流中的能量损失，是在管件附近

的局部范围

内主要由流体微团的碰撞、流体中产生的漩涡等造成的损失。

粘性底层：由于靠近管壁紊流脉动受到限制，粘滞力的作用增强，在紧贴管壁很

薄的流层中

紊流脉动消失，粘滞力的阻滞作用使流速急剧下降，速度分布比较陡峭，速度梯

度大。

水利光滑：粘性底层完全淹没了管壁的粗糙凸出部分。

莫迪图的五个区域：1、层流区。2、临界区。3、光滑管区。4、过渡区。5、完

全紊流粗糙

管区。

局部损失原因：1、管道截面突然扩大。原因一：流体惯性形成漩涡，漩涡的运

动。

原因二：流速由大变小，产生碰撞。

2、管道截面突然缩小。原因一：流体惯性产生漩涡，漩涡的运

动。

原因二：在流线弯曲、流体加速和减速

过程中，流体的碰撞、速度变

化等。

3、弯管。 原因一：由切向应力产生的沿程损失，

特别是在流动方向改变、流速

分布变化中产生的损失。

原因二：形成漩涡所产生的损失。 原因三： 由二次流形成的双螺旋流动所

产生的损失。

水击现象：在压力管道中，由于液体流速的急剧改变，从而造成瞬时压力显著、 反复、迅速变化的现象，称为水击，也称水锤。

产生的原因： 当压力管道的阀门突然关闭或开启时，当水泵突然停止 或启动时，因瞬时流速发生急剧变化，引起液体动量迅速改变，而使压力显著变化。管道上止回阀失灵，也会发生水击现象。在蒸汽管道中，若暖管不充分，疏水不彻底，导致送出的蒸汽部分凝结成水，体积突然缩小，造成局部真空，周围介质 将高速向此处冲击，也会发出巨大的音响和振动。

预防措施：1、避免直接水击，可采取增加阀门起闭时间；

2、 采用过载保护，在管道上装设安全阀门或空气室以缓冲

水击压强；

3、尽量缩短管道的长度，减低管内流速，使用弹性好的管

道。

第七章 气体的一维流动

激波：当超声速气流绕过大的障碍物时,气流在障碍物前将受到急剧的压缩,它的压强、温度、密度都将突跃地升高，而速度则突跃地降低，这种流动参数发生突

跃变化的强压缩波。

正激波前后气流速度的特点和关系：1、气流经过激波，速度降低，动量减小，熵值增加，因而必有作用在气流上与来流方向相反的力；2、引起激波的物体，必然受到与上述作用力大小相等、与来流方向相同的反作用力，即气流作用在物体上的阻力，这种阻力因激波的存在而产生，称为波阻。3、激波越强，波阻越大。

激波强弱判定：1、压强比。2、来流马赫数。

第八章 理想流体的有旋运动和无旋运动

流体微团的运动由三部分组成：1平移运动2旋转运动3含有线变形和角变形的

变形运动。

判断有旋无旋：流体微团的旋转角速度等于零的流动为无旋。

欧拉方程的意义：在流场的某点，单位质量流体的当地加速度与迁移加速度之和等于作用在它上面的重力与压力之和。

涡线：任一时刻，涡线上每一点的切向量都与该点的涡向量相切。

dx

涡管：某一时刻，由涡线组成的管状曲面。

涡束：截面积无限小的涡管。

涡通量：旋转角速度的值与垂直于 J??x(x,y,z,t)?dy?y(x,y,z,t)?dz?z(x,y,z,t)??Ω?dA???2?

AndA

角速度方向的微源涡管横截面积的乘积的两倍。

涡量场的通量（涡强）。

速度环量：速度在某一封闭周线切线上的分量

沿该封闭周线的积分。 ?K??v?ds?K?vxdx?vydy?vzdz?

工程流体力学相关概念公式 17_流体力学公式

斯托克斯定理：涡通量和速度环量都是反映旋涡作用的强弱。

平面涡流：前提：重力作用，理想不可压流体。

一无限长，涡通量为J的铅直涡束，像刚体一样以等角速度ω绕自身轴旋转。涡束周围的流体受涡束的诱导将绕涡束轴做对应的等速圆周运动。

涡束内的流动为有旋流动，称为涡核区；

涡束外的流动为无旋流动，称为环流区。

均匀等速流：流线平行，流速相等。

源流：在无限平面上，流体从一点沿径向直线均匀向各方流出，

汇流：若流体沿径向直线均匀从各方流入一点，称为汇流。

第九章 粘性流体绕过物体的流动

边界层：在大雷诺数下紧靠物体表面流速从零急剧增加到与来流速度相同数量级的薄层。

特点：1与物体的特征长度相比，边界层的厚度很小；

2边界层沿流体流动方向逐渐增厚，其外边界不与流线重合；

3沿壁面法线方向边界层被的速度梯度很大；

4在边界内层黏滞力与惯性力属同一数量级；

5沿壁面法线方向边界层内各点的压强相等，都等于主流在边界层

外边界对应点上 的压强；

6边界层内流体的流动也有层流和湍流两种流动状态。

位移厚度：被挤入主流，使主流增加了厚度为?1的一层流体，故称?1为位移厚度。

动量损失厚度：主流减去入流动量便是边界层内因黏性减速而减少的动量，故称

为动量损失厚度。

边界层分离又称为流动分离，是指原来紧贴壁面流动的边界层脱离壁面的现象。

（1）沿曲面的流速先升高后降低，相应压强先降低后升高；

（2）边界层内流体微团被粘滞力阻滞，动能损耗，逐渐减速，边界层逐渐增厚，动量逐渐被损耗尽，越来越多被停滞的流体微团在壁面和主流之间堆积；

（3）同时压强继续升高使部分流体微团向相反方向流动。造成边界层分离。分离时形成旋涡。

边界层是一个薄层，它紧靠物面，沿壁面法线方向存在着很大的速度梯度和旋度的流动区域。粘性应力对边界层的流体来说是阻力，所以随着流体沿物面向后流动，边界层内的流体会逐渐减速，增压。由于流体流动的连续性，边界层会变厚以在同一时间内流过更多的低速流体。因此边界层内存在着正压梯度，流动在正压梯度作用下，会进一步减速，最后整个边界层内的流体的动能都不足以长久的维持流动一直向下游进行，以致在物体表面某处其速度会与势流的速度方向相反，即产生逆流。该逆流会把边界层向势流中排挤，造成边界层突然变厚或分离。边界层分离之后，它将从紧靠物面的地方抬起进入主流，与主流发生参混。结果是整个参混区域的压力趋于一致。

物体阻力：阻力是由流体绕过物体流动产生的切向应力和压强造成的。

减阻方法：（1）使物体上层流边界层尽可能长，即使层流边界层转变为湍流边界

层的转折点尽可能往后推移。

（2）采用尽可能小的尾涡区的物体外形，使边界层分离向后推移。

（3）控制边界层，防止边界层分离。

卡门涡街：Re>60，形成几乎稳定的、非对称性的、多少有些规则的、旋转方向相反地交替漩涡。即旋涡交替脱落，形成涡街。

本文标题：流体力学公式-板式塔流体力学特性的测定
本文地址： http://www.61k.com/1103925.html