一 : 一次远足活动中,一部分人步行,另一部分乘一辆车,两部分人同地出发.步行者比汽车提前30分钟出发,这辆汽车到达目的地后,再回头接不行这部分人.出发地到目的地的距离是20千米.问：步行者在出发后经多少时间与回头接他们的汽车相遇？（汽车掉头的时间不计,汽车60千米一时,步行5千米一时）

一次远足活动中,一部分人步行,另一部分乘一辆车,两部分人同地出发.步行者比汽车提前30分钟出发,这辆汽车到达目的地后,再回头接不行这部分人.出发地到目的地的距离是20千米.问：步行者在出发后经多少时间与回头接他们的汽车相遇?（汽车掉头的时间不计,汽车60千米一时,步行5千米一时）

一次远足活动中,一部分人步行,另一部分乘一辆车,两部分人同地出发.步行者比汽车提前30分钟出发,这辆汽车到达目的地后,再回头接不行这部分人.出发地到目的地的距离是20千米.问：步行者在出发后经多少时间与回头接他们的汽车相遇？（汽车掉头的时间不计,汽车60千米一时,步行5千米一时）的参考答案

1)步行者出发30分钟,也就是1/2小时,走了5/2km=2.5km

2)汽车开到目的地,走了20/60=1/3小时,步行者又走了5/3km=1.667km

3)汽车返回头接步行者,时间为(20-5/2-5/3)/(60+5)= (120/6-15/6-10/6)/65=0.244小时

总时间=1/2+1/3+0.244小时

二 : 在一次远足活动中，小聪由甲地步行到乙地后原路返回，小明由甲地步行到乙地后原路返回，到达途中的丙地时发

在一次远足活动中，小聪由甲地步行到乙地后原路返回，小明由甲地步行到乙地后原路返回，到达途中的丙地时发现物品可能遗忘在乙地，于是从丙返回乙地，然后沿原路返回，两人同时出发，步行过程中保持匀速，设步行的时间为t（h），两人离甲地的距离分别为S1（km）和S2（km），图中的折线分别表示S1、S2与t之间的函数关系。 （1）甲、乙两地之间的距离为______km，乙、丙两地之间的距离为_______km； （2）分别求出小明由甲地出发首次到达乙地及由乙地到达丙地所用的时间； （3）求图中线段AB所表示的S2与t间的函数关系式，并写出自变量t的取值范围。

题型：解答题难度：偏难来源：江苏模拟题

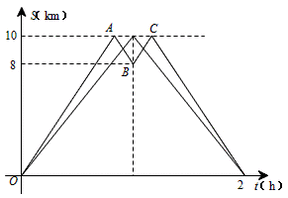解：（1）10，2； （2）v2=（10+2）÷1=12，t1=10÷12=，t2=2÷12=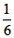， ∴小明由甲地出发首次到达乙地用了小时，由乙地到达丙地用了小时； （3）设线段AB所表示的S2与之间的函数关系式为S2=kt+b（k≠0）， 由（1）可知点A、B的坐标为A（，10），B（1，8），代入，得， 解得：， ∴S2=-12t+20（）。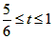

考点：

考点名称：求一次函数的解析式及一次函数的应用待定系数法求一次函数的解析式：
先设出函数解析式，再根据条件确定解析式中的未知系数，从而得到函数的解析式的方法。

一次函数的应用：
应用一次函数解应用题，一般是先写出函数解析式，在依照题意，设法求解。
（1）有图像的，注意坐标轴表示的实际意义及单位；
（2）注意自变量的取值范围。

用待定系数法求一次函数解析式的四个步骤：
第一步（设）：设出函数的一般形式。（称一次函数通式）
第二步（代）：代入解析式得出方程或方程组。
第三步（求）：通过列方程或方程组求出待定系数k，b的值。
第四步（写）：写出该函数的解析式。

一次函数的应用涉及问题：
一、分段函数问题
分段函数是在不同区间有不同对应方式的函数，要特别注意自变量取值范围的划分，既要科学合理，又要符
合实际。

二、函数的多变量问题
解决含有多变量问题时，可以分析这些变量的关系，选取其中一个变量作为自变量，然后根据问题的条件寻
求可以反映实际问题的函数

三、概括整合
（1）简单的一次函数问题：①建立函数模型的方法；②分段函数思想的应用。
（2）理清题意是采用分段函数解决问题的关键。

生活中的应用：
1.当时间t一定，距离s是速度v的一次函数。s=vt。
2.如果水池抽水速度f一定，水池里水量g是抽水时间t的一次函数。设水池中原有水量S。g=S-ft。
3.当弹簧原长度b（未挂重物时的长度）一定时，弹簧挂重物后的长度y是重物重量x的一次函数，即y=kx+b（k为任意正数）

一次函数应用常用公式：
1.求函数图像的k值：（y₁-y₂)/(x₁-x₂)
2.求与x轴平行线段的中点：(x₁+x₂)/2
3.求与y轴平行线段的中点：(y₁+y₂)/2
4.求任意线段的长：√[(x₁-x₂)²+(y₁-y₂)²]
5.求两个一次函数式图像交点坐标：解两函数式
两个一次函数 y₁=k₁x+b₁; y₂=k₂x+b₂令y₁=y₂ 得k₁x+b₁=k₂x+b₂将解得的x=x0值代回y₁=k₁x+b₁; y₂=k₂x+b₂两式任一式 得到y=y₀则(x₀,y₀)即为 y₁=k₁x+b₁ 与 y₂=k₂x+b₂交点坐标
6.求任意2点所连线段的中点坐标：[（x₁+x₂）/2，（y₁+y₂）/2]
7.求任意2点的连线的一次函数解析式：（x-x₁）/(x₁-x₂)=(y-y₁)/(y₁-y₂) (若分母为0，则分子为0)
（x,y）为 + ，+（正，正）时该点在第一象限
（x,y）为 - ，+（负，正）时该点在第二象限
（x,y）为 - ，-（负，负）时该点在第三象限
（x,y）为 + ，-（正，负）时该点在第四象限
8.若两条直线y₁=k₁x+b₁//y₂=k₂x+b₂，则k₁=k₂，b₁≠b₂
9.如两条直线y₁=k₁x+b₁⊥y₂=k₂x+b₂，则k₁×k₂=-1
10.
y=k（x-n）+b就是直线向右平移n个单位
y=k（x+n）+b就是直线向左平移n个单位
y=kx+b+n就是向上平移n个单位
y=kx+b-n就是向下平移n个单位
口决：左加右减相对于x，上加下减相对于b。
11.直线y=kx+b与x轴的交点：(-b/k，0) 与y轴的交点：(0，b)

考点名称：函数的图像

函数图象的概念：
对于一个函数，如果把自变量x和函数y的每对对应值分别作为点的横坐标与纵坐标，在坐标平面内描出相应的点，这些点所组成的图形，就是这个函数的图象．

由函数解析式画其图象的一般步骤：
①列表：列表给出自变量与函数的一些对应值；
②描点：以表中每对对应值为坐标，在坐标平面内描出相应的点；
③连线：按照自变量由小到大的顺序，把所描各点用平滑的曲线连接起来．

利用函数的图象解决实际问题，其关键是正确识别横轴和纵轴的意义，正确理解函数图象的性质，正确地识图、用图．

函数图象上的点的坐标与其解析式之间的关系：
①由图象的定义可知图象上任意一点P（x，y）中的x，y是解析式方程的一个解，反之，以解析式方程的任意一个解为坐标的点一定在函数图象上；
②通常判定点是否在函数图象上的方法是：将这个点的坐标代入函数解析式，如果满足函数解析式，这个点就在函数的图象上，如果不满足函数解析式，这个点就不在其函数的图象上，反之亦然；
③两个函数图像的交点就是饿两个函数解析式所组成的方程组的解。

三 : 在一次远足活动中，某班学生分成两组，第一组由甲地匀速步行到乙地后原路返回，第二组由甲地匀速步行经乙地

在一次远足活动中，某班学生分成两组，第一组由甲地匀速步行到乙地后原路返回，第二组由甲地匀速步行经乙地继续前行到丙地后原路返回，两组同时出发，设步行的时间为t（h），两组离乙地的距离分别为s1（km）、s2（km），图中的折线分别表示s1、s2与t之间的函数关系。 （1）甲、乙两地之间的距离为______km，乙、丙两地之间的距离为____ km； （2）求第二组由甲地出发首次到达乙地及由乙地到达丙地所用的时间分别是多少？ （3）求图中线段AB所表示的s2与t之间的函数关系式，并写出自变量t的取值范围。

题型：解答题难度：偏难来源：湖南省中考真题

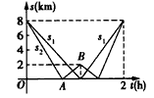解：（1）8，2； （2）第二组由甲地出发首次到达乙地所用的时间为： 8÷[2×（8+2）÷2]=8÷10=0.8（小时）， 第二组由乙地到达丙地所用的时间为： 2÷[2×（8+2）÷2]=2÷10=0.2（小时）； （3）根据题意得A、B的坐标分别为（0.8，0）和（1，2）， 设线段AB的函数关系式为：s2=kt+b， 根据题意得： 解得： ∴图中线段AB所表示的s2与t之间的函数关系式为：s2=10t-8，自变量t的取值范围是：0.8≤t≤1。

考点：

考点名称：求一次函数的解析式及一次函数的应用待定系数法求一次函数的解析式：
先设出函数解析式，再根据条件确定解析式中的未知系数，从而得到函数的解析式的方法。

一次函数的应用：
应用一次函数解应用题，一般是先写出函数解析式，在依照题意，设法求解。
（1）有图像的，注意坐标轴表示的实际意义及单位；
（2）注意自变量的取值范围。

用待定系数法求一次函数解析式的四个步骤：
第一步（设）：设出函数的一般形式。（称一次函数通式）
第二步（代）：代入解析式得出方程或方程组。
第三步（求）：通过列方程或方程组求出待定系数k，b的值。
第四步（写）：写出该函数的解析式。

一次函数的应用涉及问题：
一、分段函数问题
分段函数是在不同区间有不同对应方式的函数，要特别注意自变量取值范围的划分，既要科学合理，又要符
合实际。

二、函数的多变量问题
解决含有多变量问题时，可以分析这些变量的关系，选取其中一个变量作为自变量，然后根据问题的条件寻
求可以反映实际问题的函数

三、概括整合
（1）简单的一次函数问题：①建立函数模型的方法；②分段函数思想的应用。
（2）理清题意是采用分段函数解决问题的关键。

生活中的应用：
1.当时间t一定，距离s是速度v的一次函数。s=vt。
2.如果水池抽水速度f一定，水池里水量g是抽水时间t的一次函数。设水池中原有水量S。g=S-ft。
3.当弹簧原长度b（未挂重物时的长度）一定时，弹簧挂重物后的长度y是重物重量x的一次函数，即y=kx+b（k为任意正数）

一次函数应用常用公式：
1.求函数图像的k值：（y₁-y₂)/(x₁-x₂)
2.求与x轴平行线段的中点：(x₁+x₂)/2
3.求与y轴平行线段的中点：(y₁+y₂)/2
4.求任意线段的长：√[(x₁-x₂)²+(y₁-y₂)²]
5.求两个一次函数式图像交点坐标：解两函数式
两个一次函数 y₁=k₁x+b₁; y₂=k₂x+b₂令y₁=y₂ 得k₁x+b₁=k₂x+b₂将解得的x=x0值代回y₁=k₁x+b₁; y₂=k₂x+b₂两式任一式 得到y=y₀则(x₀,y₀)即为 y₁=k₁x+b₁ 与 y₂=k₂x+b₂交点坐标
6.求任意2点所连线段的中点坐标：[（x₁+x₂）/2，（y₁+y₂）/2]
7.求任意2点的连线的一次函数解析式：（x-x₁）/(x₁-x₂)=(y-y₁)/(y₁-y₂) (若分母为0，则分子为0)
（x,y）为 + ，+（正，正）时该点在第一象限
（x,y）为 - ，+（负，正）时该点在第二象限
（x,y）为 - ，-（负，负）时该点在第三象限
（x,y）为 + ，-（正，负）时该点在第四象限
8.若两条直线y₁=k₁x+b₁//y₂=k₂x+b₂，则k₁=k₂，b₁≠b₂
9.如两条直线y₁=k₁x+b₁⊥y₂=k₂x+b₂，则k₁×k₂=-1
10.
y=k（x-n）+b就是直线向右平移n个单位
y=k（x+n）+b就是直线向左平移n个单位
y=kx+b+n就是向上平移n个单位
y=kx+b-n就是向下平移n个单位
口决：左加右减相对于x，上加下减相对于b。
11.直线y=kx+b与x轴的交点：(-b/k，0) 与y轴的交点：(0，b)

本文标题：在一次远足活动中-一次远足活动中,一部分人步行,另一部分乘一辆车,两部分人同地出发.步行者比汽车提前30分钟出发,这辆汽车到达目的地后,再回头接不行这部分人.出发地到目的地的距离是20千米.问：步行者在出发后经多少时间与回头接他们的汽车相遇？（汽车掉头的时间不计,汽车60千米一时,步行5千米一时）
本文地址： http://www.61k.com/1101478.html