一 : 对于气温，有的地方用摄氏温度表示，有的地方用华氏温度表示，摄氏温度与华氏温度之间存在一次函数关系。从

对于气温，有的地方用摄氏温度表示，有的地方用华氏温度表示，摄氏温度与华氏温度之间存在一次函数关系。从温度计的刻度上可以看出，摄氏温度x（℃）与华氏温度y（℉）有如下的对应关系：

x（℃） … -10 0 10 20 30 … y（℉） … 14 32 50 68 86 … （1）试确定y与x之间的函数关系式，并画出函数图象； （2）某天，南昌的最高气温是25℃，澳大利亚悉尼的最高气温80℉，这一天哪个地区的最高气温较高？

题型：解答题难度：中档来源：同步题

解：（1）y与x之间的函数关系式为y=1.8x+32，图“略”； （2）由（1）知，南昌的华氏温度为77℉，所以可知这一天悉尼的最高气温较高。

考点：

考点名称：一次函数的图像函数不是数，它是指某一变化过程中两个变量之间的关系
一次函数的图象：一条直线，过（0，b），（，0）两点。

性质：
（1）在一次函数图像上的任取一点P（x，y），则都满足等式：y=kx+b(k≠0)。
（2）一次函数与y轴交点的坐标总是（0，b)，与x轴总交于（-b/k，0）。正比例函数的图像都经过原点。

k，b决定函数图像的位置：
y=kx时，y与x成正比例：
当k>0时，直线必通过第一、三象限，y随x的增大而增大；
当k<0时，直线必通过第二、四象限，y随x的增大而减小。
y=kx+b时：
当 k>0，b>0， 这时此函数的图象经过第一、二、三象限；
当 k>0，b<0，这时此函数的图象经过第一、三、四象限；
当 k<0，b>0，这时此函数的图象经过第一、二、四象限；
当 k<0，b<0，这时此函数的图象经过第二、三、四象限。
当b>0时，直线必通过第一、二象限；
当b<0时，直线必通过第三、四象限。
特别地，当b=0时，直线经过原点O（0，0）。
这时，当k>0时，直线只通过第一、三象限，不会通过第二、四象限。
当k<0时，直线只通过第二、四象限，不会通过第一、三象限。

特殊位置关系：
当平面直角坐标系中两直线平行时，其函数解析式中k的值（即一次项系数）相等；
当平面直角坐标系中两直线垂直时，其函数解析式中k的值互为负倒数（即两个k值的乘积为-1）一次函数的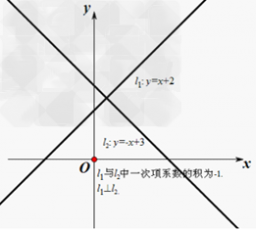

画法：
（1）列表：表中给出一些自变量的值及其对应的函数值。
（2）描点：在直角坐标系中，以自变量的值为横坐标，相应的函数值为纵坐标，描出表格中数值对应的各点。
一般地，y=kx+b(k≠0）的图象过（0，b）和（-b/k，0）两点即可画出。
正比例函数y=kx(k≠0）的图象是过坐标原点的一条直线，一般取（0，0）和（1，k）两点画出即可。
（3）连线： 按照横坐标由小到大的顺序把描出的各点用直线连接起来。
考点名称：求一次函数的解析式及一次函数的应用待定系数法求一次函数的解析式：
先设出函数解析式，再根据条件确定解析式中的未知系数，从而得到函数的解析式的方法。

一次函数的应用：
应用一次函数解应用题，一般是先写出函数解析式，在依照题意，设法求解。
（1）有图像的，注意坐标轴表示的实际意义及单位；
（2）注意自变量的取值范围。

用待定系数法求一次函数解析式的四个步骤：
第一步（设）：设出函数的一般形式。（称一次函数通式）
第二步（代）：代入解析式得出方程或方程组。
第三步（求）：通过列方程或方程组求出待定系数k，b的值。
第四步（写）：写出该函数的解析式。

一次函数的应用涉及问题：
一、分段函数问题
分段函数是在不同区间有不同对应方式的函数，要特别注意自变量取值范围的划分，既要科学合理，又要符
合实际。

二、函数的多变量问题
解决含有多变量问题时，可以分析这些变量的关系，选取其中一个变量作为自变量，然后根据问题的条件寻
求可以反映实际问题的函数

三、概括整合
（1）简单的一次函数问题：①建立函数模型的方法；②分段函数思想的应用。
（2）理清题意是采用分段函数解决问题的关键。

生活中的应用：
1.当时间t一定，距离s是速度v的一次函数。s=vt。
2.如果水池抽水速度f一定，水池里水量g是抽水时间t的一次函数。设水池中原有水量S。g=S-ft。
3.当弹簧原长度b（未挂重物时的长度）一定时，弹簧挂重物后的长度y是重物重量x的一次函数，即y=kx+b（k为任意正数）

一次函数应用常用公式：
1.求函数图像的k值：（y₁-y₂)/(x₁-x₂)
2.求与x轴平行线段的中点：(x₁+x₂)/2
3.求与y轴平行线段的中点：(y₁+y₂)/2
4.求任意线段的长：√[(x₁-x₂)²+(y₁-y₂)²]
5.求两个一次函数式图像交点坐标：解两函数式
两个一次函数 y₁=k₁x+b₁; y₂=k₂x+b₂令y₁=y₂ 得k₁x+b₁=k₂x+b₂将解得的x=x0值代回y₁=k₁x+b₁; y₂=k₂x+b₂两式任一式 得到y=y₀则(x₀,y₀)即为 y₁=k₁x+b₁ 与 y₂=k₂x+b₂交点坐标
6.求任意2点所连线段的中点坐标：[（x₁+x₂）/2，（y₁+y₂）/2]
7.求任意2点的连线的一次函数解析式：（x-x₁）/(x₁-x₂)=(y-y₁)/(y₁-y₂) (若分母为0，则分子为0)
（x,y）为 + ，+（正，正）时该点在第一象限
（x,y）为 - ，+（负，正）时该点在第二象限
（x,y）为 - ，-（负，负）时该点在第三象限
（x,y）为 + ，-（正，负）时该点在第四象限
8.若两条直线y₁=k₁x+b₁//y₂=k₂x+b₂，则k₁=k₂，b₁≠b₂
9.如两条直线y₁=k₁x+b₁⊥y₂=k₂x+b₂，则k₁×k₂=-1
10.
y=k（x-n）+b就是直线向右平移n个单位
y=k（x+n）+b就是直线向左平移n个单位
y=kx+b+n就是向上平移n个单位
y=kx+b-n就是向下平移n个单位
口决：左加右减相对于x，上加下减相对于b。
11.直线y=kx+b与x轴的交点：(-b/k，0) 与y轴的交点：(0，b)

二 : 华氏温度f（℉）与摄氏温度c（℃）之间存在如下的关系：f=c+32。（1）一个人的体温有可能达到10

华氏温度f（℉）与摄氏温度c（℃）之间存在如下的关系：f =c+32。 （1）一个人的体温有可能达到100℉吗？ （2）若某地早晨的温度为15℃，那么此地早晨的华氏温度是多少度？ （3）若当地某一时刻的温度为68℉，则该时刻摄氏温度是多少？

题型：解答题难度：中档来源：竞赛题

人的体温一般在37～38℃ （1）c=30=100，c=37，有可能 （2）f =×15℃+32=59℉ （3）c+32=68，c=20℃

考点：

考点名称：分数的四则混合运算及应用

运算顺序：
分数四则混合运算的运算顺序和整数则混合运算的运算顺序相同：
一个算式里，如果只含有两级运算，先算第一级运算，再算第二级运算。
在含有括号的算式里，先算小括号里面的，再算中括号里面的，最后算括号外面的。

计算法则：
分数乘法的意义：
分数乘以整数 —×12 表示12个—是多少。
整数乘以真分数 12×— 表示12的—是多少。
分数乘以真分数 —×— —的—是多少。
一个数乘以带分数 —×1— 表示—的1—倍是多少。

分数加、减法的计算法则：
同分母分数相加减，分母不变，分子相加减。
异分母分数相加减，先通分，再按同分母方法计算。

分数乘除法计算方法：
分数乘法，分子相乘作分子，分母相乘作分母。
分数除法，乘以除数的倒数。

分数四则运算的意义:
加法:
把两个数合并成一个数的运算 把两个小数合并成一个小数的运算 把两个分数合并成一个分数的运算;
减法:
已知两个加数的和与其中一个加数，求另一个加数的运算 已知两个加数的和与其中一个加数，求另一个加数的运算 已知两个加数的和与其中一个加数，求另一个加数的运算;
乘法:
求几个相同加数的和的简便运算,小数乘整数的意义与整数乘法意义相同;
一个数乘纯小数就是求这个数的十分之几，百分之几……
除法:
已知两个因数的积与其中一个因数，求另一个因数的运算,与整数除法的意义相同.

三 : 对于气温，有的地方用摄氏温度表示，有的地方用华氏温度表示，摄氏温度与华氏温度之间存在着某种函数关系，

对于气温，有的地方用摄氏温度表示，有的地方用华氏温度表示，摄氏温度与华氏温度之间存在着某种函数关系，从温度计上可以看出摄氏（℃）温度x与华氏（℉）温度y有如下表所示的对应关系，则确定y与x之间的函数关系式是（　　） x（℃） … -10 0 10 20 30 … y（℉） … 14 32 50 68 86 … A．y=x B．y=1.8x+32 C．y=0.56x2+7.4x+32 D．y=2.1x+26

题型：单选题难度：偏易来源：济南

B

考点：

考点名称：求一次函数的解析式及一次函数的应用待定系数法求一次函数的解析式：
先设出函数解析式，再根据条件确定解析式中的未知系数，从而得到函数的解析式的方法。

一次函数的应用：
应用一次函数解应用题，一般是先写出函数解析式，在依照题意，设法求解。
（1）有图像的，注意坐标轴表示的实际意义及单位；
（2）注意自变量的取值范围。

用待定系数法求一次函数解析式的四个步骤：
第一步（设）：设出函数的一般形式。（称一次函数通式）
第二步（代）：代入解析式得出方程或方程组。
第三步（求）：通过列方程或方程组求出待定系数k，b的值。
第四步（写）：写出该函数的解析式。

一次函数的应用涉及问题：
一、分段函数问题
分段函数是在不同区间有不同对应方式的函数，要特别注意自变量取值范围的划分，既要科学合理，又要符
合实际。

二、函数的多变量问题
解决含有多变量问题时，可以分析这些变量的关系，选取其中一个变量作为自变量，然后根据问题的条件寻
求可以反映实际问题的函数

三、概括整合
（1）简单的一次函数问题：①建立函数模型的方法；②分段函数思想的应用。
（2）理清题意是采用分段函数解决问题的关键。

生活中的应用：
1.当时间t一定，距离s是速度v的一次函数。s=vt。
2.如果水池抽水速度f一定，水池里水量g是抽水时间t的一次函数。设水池中原有水量S。g=S-ft。
3.当弹簧原长度b（未挂重物时的长度）一定时，弹簧挂重物后的长度y是重物重量x的一次函数，即y=kx+b（k为任意正数）

一次函数应用常用公式：
1.求函数图像的k值：（y₁-y₂)/(x₁-x₂)
2.求与x轴平行线段的中点：(x₁+x₂)/2
3.求与y轴平行线段的中点：(y₁+y₂)/2
4.求任意线段的长：√[(x₁-x₂)²+(y₁-y₂)²]
5.求两个一次函数式图像交点坐标：解两函数式
两个一次函数 y₁=k₁x+b₁; y₂=k₂x+b₂令y₁=y₂ 得k₁x+b₁=k₂x+b₂将解得的x=x0值代回y₁=k₁x+b₁; y₂=k₂x+b₂两式任一式 得到y=y₀则(x₀,y₀)即为 y₁=k₁x+b₁ 与 y₂=k₂x+b₂交点坐标
6.求任意2点所连线段的中点坐标：[（x₁+x₂）/2，（y₁+y₂）/2]
7.求任意2点的连线的一次函数解析式：（x-x₁）/(x₁-x₂)=(y-y₁)/(y₁-y₂) (若分母为0，则分子为0)
（x,y）为 + ，+（正，正）时该点在第一象限
（x,y）为 - ，+（负，正）时该点在第二象限
（x,y）为 - ，-（负，负）时该点在第三象限
（x,y）为 + ，-（正，负）时该点在第四象限
8.若两条直线y₁=k₁x+b₁//y₂=k₂x+b₂，则k₁=k₂，b₁≠b₂
9.如两条直线y₁=k₁x+b₁⊥y₂=k₂x+b₂，则k₁×k₂=-1
10.
y=k（x-n）+b就是直线向右平移n个单位
y=k（x+n）+b就是直线向左平移n个单位
y=kx+b+n就是向上平移n个单位
y=kx+b-n就是向下平移n个单位
口决：左加右减相对于x，上加下减相对于b。
11.直线y=kx+b与x轴的交点：(-b/k，0) 与y轴的交点：(0，b)

四 : 鱼摄食的水温与水质

水温和水质是影响鱼类生长和摄食的主要因素。根据鱼的特性和冷热，给鱼池搞好排灌，以浅水增温，深水保温、换水调温增氧的方法，调节水温水质，提高产量。 水温草、鲢、青、鲤鱼，适宜生长的温度20一32℃，其中最适繁殖的温度22—26℃，最适摄食和生长的温度25—32℃。草鱼在水温27—30℃时摄食量最大，20℃时摄食量最低，低于5℃时则停止摄食。鲤鱼最适摄食温度23—29℃，3—4℃时停止摄食。这些鱼当水温低于0．5℃或高于40℃时，便不能生存。鲢鱼在水温低于7℃时便会死亡。 水质草鱼、青鱼适合在较清瘦的水中生长，鲤鱼，鲫鱼适合肥水，各种鱼都要求水中有足够的溶氧量。在适宜的环境中，水中溶氧量越高，鱼的摄食量越大，生长也快。

本文标题：摄氏度与华氏温度-对于气温，有的地方用摄氏温度表示，有的地方用华氏温度表示，摄氏温度与华氏温度之间存在一次函数关系。从
本文地址： http://www.61k.com/1100408.html