一 : 连通性：连通性-定义，连通性-性质

连通性，是点集拓扑学中的基本概念。

连通性_连通性 -定义

连通性是点集拓扑学中的基本概念。

其定义如下：

称拓扑空间X为连通的，若X中除了空集和X本身外没有别的既开又闭子集。

拓扑空间X的子集E称为连通的，若E作为X的子空间在诱导拓扑下是连通的。等价描述

1. 称拓扑空间X连通，若X不能表示成2个非空不交开集的并。

2. 称拓扑空间X连通，若当它分成2个非空子集的并A∪B时，有A交B的闭包非空，或B交A的闭包非空。

3.称拓扑空间X连通，若X内即开又闭的子集只有X与空集。

连通性_连通性 -性质

【连通的性质】

1. 实数集的子集是连通的，当且仅当它是1个区间

2. 连通性由同胚保持，从而是空间的拓扑性质

3. 设Ω是X的一族子集，它们的并是整个空间X，每个Ω中的成员连通，且两两不分离（即任意2个集合的闭包有非空交），则X连通

4. 若X,Y连通，则乘积空间X×Y连通

连通性_连通性 -其他相关概念

1. 道路连通：

称X为道路连通的，若任取X中的两点x,y，有连接x,y的道路

2. 局部道路连通

称X为局部道路连通的，若对任意X中的点x,x的任一领域U包含x的1个道路连通邻域V

3. 局部连通

称X为局部连通的，若对任意X中的点x,x的任一领域U包含x的1个连通邻域V

道路连通空间一定是连通的，反之不然。

道路连通与局部道路连通之间没有必然联系。

连通与局部连通之间没有必然联系。

二 : 静电场：静电场-定义，静电场-性质

静电场（electrostatic field），是由静止电荷(相对于观察者静止的电荷)激发的电场。它是电荷周围空间存在的一种特殊形态的物质，其基本特征是对置于其中的静止电荷有力的作用。库仑定律描述了这个力。 有介质时的静电场是由束缚电荷及自由电荷共同产生的，为了表示这二者共同作用下的电场，可以引入另一个场矢量电通量密度D（又称电位移）。可以证明，当已知ρ、ε及边界条件时，泊松方程或拉普拉斯方程的解是惟一的，可以设法求解电位φ，再求出场中各处的E。

静电场_静电场 -定义

高中静电场知识概括

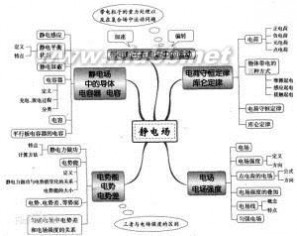
由静止电荷(相对于观察者静止的电荷)激发的电场。

静电场_静电场 -性质

根据静电场的高斯定理：

静电场

静电场的电场线起于正电荷或无穷远,

终止于负电荷或无穷远，故静电场是有源场．

从安培环路定理来说它是1个无旋场．

根据环量定理，静电场中环量恒等于零,表明静电场中沿任意闭合路径移动电荷，电场力所做的功都为零，因此静电场是保守场．

根据库仑定律，2个点电荷之间的作用力跟它们的电荷量的乘积成正比，和它们距离的平方成反比，作用力的方向在它们的连线上，即F=（k·q1q2）/r2;,其中q1、q2为两电荷的电荷量（不计正负性）、k为静电力常量，约为9.0e+09（牛顿）/（库伦;），r为两电荷中心点连线的距离。注意，点电荷是不考虑其尺寸、形状和电荷分布情况的带电体。是实际带电体的理想化模型。当带电体的距离比它们的大小大得多时，带电体的形状和大小可以忽略不计的点电荷。

静电场_静电场 -静电感应

1个带电的物体靠近另1个导体时，导体的电荷分别发生明显的变化，物理学中把这种现象叫做静电感应。

静电场

如果电场中存在导体，在电场力的作用下出现静电感应现象,使原

来中和的正、负电荷分离,出现在导体表面上。这些电荷称为感应电荷。总的电场是感应电荷与自由电荷共同作用结果。达到平衡时，导体内部的场强处处为零,导体是1个等势体，导体表面是等势面，感应电荷都分布在导体外表面，导体表面的电场方向处处与导体表面垂直。静电感应现象有一些应用，但也可能造成危害。

静电场_静电场 -场中介质

静电场知识结构图

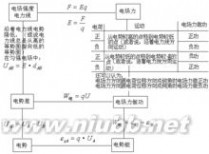
电场中的绝缘介质又称为电介质。由于电场力的作用在原子尺度上

出现了等效的束缚电荷。这种现象称为电介质的极化。对1种绝缘材料，当电场强度超过某一数值时，束缚电荷被迫流动造成介质击穿而失去其绝缘性能。因此静电场的大小对电工器件的设计及材料选择十分重要。 有介质时的静电场是由束缚电荷及自由电荷共同产生的，为了表示这二者共同作用下的电场，可以引入另1个场矢量电通量密度D（又称电位移）。它定义为

式中P为电介质的极化强度，则可得高斯通量定理

公式

式中q仅为S面内所有自由电荷，而不包括电介质的束缚电荷。高斯通量定理的微分形式为电位移的散度等于该点自由电荷（体）密度ρ，

电介质的极化强度P与电场强度E有关，而电通量密度又与P和E有关，故可得表示电介质的本构方程

D=εE

静电场_静电场 -电位

由于静电场是无旋场,故可用标量电位φ表征静电场（见电位）。电位与电场强度的关系是

式中Q点为电位参考点，可选在无穷远处；P点为观察点。上式的微分形式为电场强度等于电位的负梯度，即

E=-墷φ在ε为常数的区域，

公式

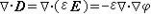
式中墷·墷可记作墷2，在直角坐标中

公式

分别为一阶与二阶微分算符。这样,可得电位φ所满足的

微分方程

称为泊松方程。如果观察点处自由电荷密度ρ为0，则

墷2φ=0

称为拉普拉斯方程。泊松方程和拉普拉斯方程描述了静电场空间分布的规律性。可以证明，当已知ρ、ε及边界条件时，泊松方程或拉普拉斯方程的解是惟一的，可以设法求解电位φ，再求出场中各处的E。

三 : 圆柱体：圆柱体-圆柱体的定义，圆柱体-性质说明

圆柱体是指在同一个平面内有一条定直线和一条动线，当这个平面绕着这条定直线旋转一周时，这条动线所成的面叫做旋转面，这条定直线叫做旋转面的轴，这条动线叫做旋转面的母线。如果用垂直于轴的两个平面去截圆柱面，那么两个截面和圆柱面所围成的几何体叫做直圆柱，既称圆柱体。

圆柱_圆柱体 -圆柱体的定义

圆柱体

1、旋转定义法：1个长方形以一边为轴顺时针或逆时针旋转一星期，所经过的空间叫

(www.61k.com)做圆柱体。

圆柱体

2、平移定义法：以1个圆为底面，上或下移动一定的距离，所经过的空间叫做圆柱体。

圆柱_圆柱体 -性质说明

1.圆柱的上 ，下2个面叫底面，周围的面（上下底面除外）叫侧面，1个圆柱体是由2个底面和1个侧面组成的。

2.圆柱体的2个底面是完全相同的2个圆面。2个底面之间的距离是圆柱体的高。

3.圆柱体的侧面是1个曲面，圆柱体的侧面的展开图是1个长方形、正方形或平行四边形（斜着切）。

圆柱的侧面积=底面周长x高，即：

S侧面积=Ch=2πrh

底面周长C=2πr=πd

圆柱的表面积=侧面积+底面积x2=2πr2+Ch=2πr（r+h)

4.圆柱的体积=底面积x高

即V=S底面积×h=(π×r×r)h

5.等底等高的圆柱的体积是圆锥的3倍

6.圆柱体可以用1个平行四边形围成

7.圆柱的表面积=圆柱的表面积=侧面积+底面积x2

8.把圆柱沿底面直径分成2个同样的部分，每1个部分叫半圆柱。这时与原来的圆柱比较，表面积不变、体积是原来的一半。

9.圆柱的轴截面是直径x高的长方形，横截面是与底面相同的圆。

圆柱_圆柱体 -公式说明

圆柱体

数学上，圆柱（古称圆堡壔、圆囷，英语：cylinder）是1个二次曲面，也就是说，1个三维曲面，满足以下直角坐标系中的方程：

这个方程是用于椭圆柱的，是对于普通圆柱（a=b）的1个推广。更一般的是柱体——横截面可以是任何曲线。

圆柱是1个退化二次曲面，因为至少有1个坐标（这里就是z）不出现在方程中。在有些定义中，圆柱面根本不视为二次曲面。

在日常使用中，圆柱指1个直圆柱的有限段，其两端闭合形成圆形表面，如右图所示。若圆柱半径为r,长度为h，则它的体积为

九章算术记载的公式是：“周自相乘，以高乘之，十二而一。”

而它的表面积为

对于给定的体积，最小表面积的圆柱满足h = 2r。对于给定的表面积，最大体积的圆柱也满足h = 2r。

也有几种不太常见的圆柱类型。这些是虚椭圆柱和双曲柱面以及抛物柱面。

本文标题：不等式的定义及性质-连通性：连通性-定义，连通性-性质
本文地址： http://www.61k.com/1095311.html