一 : 1966年 “金星”3号着陆

 

金星3号探测器

 

“金星”号探测器属于苏联行星和行星际探测器系列，主要任务是探测金星和金星周围空间。从1961年2月到1983年6月，“金星”号探测器共发射了16个，其中2个飞过金星，4个飞抵金星表面，另外10个在金星表面实现了着陆。

2和3号首次完成双星飞行，它们分别于1965年11月12日和16日发射，2号于1966年2月27日在距金星24000公里处飞过。3号于3月1日在金星表面硬着陆，偏离预计着陆点约450公里。

“金星”号探测器由轨道舱和着陆舱组成。探测器在着陆舱向金星表面降落期间探测金星大气的压力、温度、密度、风速、照度、云层结构和大气的化学成分，着陆后直接测量金星表面的各种参数，并考察了金星表层土壤，在着陆点钻探金星岩层，完成岩样的化学分析。探测器的轨道舱除用数据遥测系统向地球发回各种测量数据外，还用电视摄像机系统拍摄了金星表面的图像，并发回地球。探测器带有定向系统、轨道修正发动机、远程无线电通信和轨道测量系统以及太阳电池阵电源系统。除1和2号外，其他探测器都有着陆系统。“金星”号探测器首先被送入停泊轨道，然后点燃末级火箭，进入飞向金星的轨道。

本作品为“科普中国-科技创新里程碑”原创 转载时务请注明出处

二 : 在勇气号火星探测器着陆的最后阶段，着陆器降落到火星表面上，再经过多次弹跳才停下来。假设着陆器第一次落

三 : 在勇气号火星探测器着陆的最后阶段，着陆器降落到火星表面上，再经过多次弹跳才下来。（已知火星的一个卫星

61阅读/ www.61k.net

在勇气号火星探测器着陆的最后阶段，着陆器降落到火星表面上，再经过多次弹跳才下来。（已知火星的一个卫星的圆轨道的半径为r，周期为T，火星可视为半径为r0的均匀球体）假设着陆器第一次落到火星表面弹起后，到达最高点时高度为h，速度方向是水平的，速度大小为v0。求： （1）火星表面的重力加速度； （2）它第二次落到火星表面时速度的大小，计算时不计火星大气阻力。

题型：计算题难度：中档来源：0103 期中题

解：（1）对于火星的卫星m： 对于火星表面的物体m0： 则： （2）设落到火星表面时的竖直速度为v1，则有： 又：v2＝v02+v12 所以：

考点：

考点名称：万有引力定律的其他应用

万有引力定律的其他应用：

万有引力定律：（G=6.67×10^-11N·m²/kg²），万有引力定律在天文学中的应用：
1、计算天体的质量和密度；
2、人造地球卫星、地球同步卫星、近地卫星；
3、发现未知天体；
4、分析重力加速度g随离地面高度h的变化情况；
①物体的重力随地面高度h的变化情况：物体的重力近似地球对物体的吸引力，即近似等于，可见物体的重力随h的增大而减小，由G=mg得g随h的增大而减小。
②在地球表面（忽略地球自转影响）：（g为地球表面重力加速度，r为地球半径）。
③当物体位于地面以下时，所受重力也比地面要小，物体越接近地心，重力越小，物体在地心时，其重力为零。
5、双星问题：天文学上把两颗相距比较近，又与其他星体距离比较远的星体叫做双星。双星的间距是一定的，它们绕二者连线上的同一点分别做圆周运动，角速度相等。以下图为例


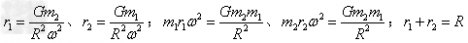
由以上各式解得：
6、黄金代换公式：GM=gR²。

考点名称：运动的合成与分解

定义：
物体的实际运动往往是由几个独立的分运动合成的，由已知的分运动求跟它们等效的合运动叫做运动的合成；由已知的合运动求跟它等效的分运动叫做运动的分解。

运动的合成与分解基本关系：
①分运动的独立性；
②运动的等效性（合运动和分运动是等效替代关系，不能并存）；
③运动的等时性；
④运动的矢量性（加速度、速度、位移都是矢量，其合成和分解遵循平行四边形定则）。

互成角度的两个分运动的合运动的判断:
合运动的情况取决于两分运动的速度的合速度与两分运动的加速度的合加速度，两者是否在同一直线上，在同一直线上作直线运动，不在同一直线上将作曲线运动。
①两个直线运动的合运动仍然是匀速直线运动；
②一个匀速直线运动和一个匀加速直线运动的合运动是曲线运动；
③两个初速度为零的匀加速直线运动的合运动仍然是匀加速直线运动；
④两个初速度不为零的匀加速直线运动的合运动可能是直线运动也可能是曲线运动。当两个分运动的初速度的合速度的方向与这两个分运动的合加速度方向在同一直线上时，合运动是匀加速直线运动，否则是曲线运动。

怎样确定合运动和分运动:
①合运动一定是物体的实际运动；
②如果选择运动的物体作为参照物，则参照物的运动和物体相对参照物的运动是分运动，物体相对地面的运动是合运动。
③进行运动的分解时，在遵循平行四边形定则的前提下，类似力的分解，要按照实际效果进行分解。例如绳端速度的分解，通常有两个原则：按效果正交分解物体运动的实际速度，沿绳方向一个分量，另一个分量垂直于绳（效果：沿绳方向的收缩速度，垂直于绳方向的转动速度）。

小船渡河问题:

小船渡河是典型的运动合成的问题。一条宽度为L的河流，水流速度为V_s，已知船在静水中的速度为V_c，那么：
①渡河时间最短：
如图甲所示，设船上头斜向上游与河岸成任意角θ，这时船速在垂直于河岸方向的速度分量V₁=V_csinθ，渡河所需时间为：。
可以看出：L、V_c一定时，t随sinθ增大而减小；当θ=90°时，sinθ=1，所以，当船头与河岸垂直时，渡河时间最短，。

②V_c>V_s，渡河路径最短：
如图乙所示，渡河的最小位移即河的宽度。为了使渡河位移等于L，必须使船的合速度V的方向与河岸垂直。这是船头应指向河的上游，并与河岸成一定的角度θ。根据三角函数关系有：Vccosθ─V_s=0。
所以θ=arccos，因为0≤cosθ≤1，所以只有在V_c>V_s时，船才有可能垂直于河岸横渡。
③V_c＜V_s，渡河路径最短：
如果水流速度大于船上在静水中的航行速度，则不论船的航向如何，总是被水冲向下游。怎样才能使漂下的距离最短呢？如图丙所示，设船头V_c与河岸成θ角，合速度V与河岸成α角。可以看出：α角越大，船漂下的距离x越短，那么，在什么条件下α角最大呢？以V_s的矢尖为圆心，以V_c为半径画圆，当V与圆相切时，α角最大，根据cosθ=，船头与河岸的夹角应为：θ=arccos。
船漂的最短距离为：。
此时渡河的最短位移为：。

四 : 在勇气号火星探测器着陆的最后阶段，着陆器降落到火星表面上，再经过多次弹跳才下来。（已知火星的一个卫星

在勇气号火星探测器着陆的最后阶段，着陆器降落到火星表面上，再经过多次弹跳才下来。（已知火星的一个卫星的圆轨道的半径为r，周期为T，火星可视为半径为r0的均匀球体）假设着陆器第一次落到火星表面弹起后，到达最高点时高度为h，速度方向是水平的，速度大小为v0。求： （1）火星表面的重力加速度； （2）它第二次落到火星表面时速度的大小，计算时不计火星大气阻力。

题型：计算题难度：中档来源：0103 期中题

解：（1）对于火星的卫星m： 对于火星表面的物体m0： 则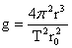： （2）设落到火星表面时的竖直速度为v1，则有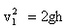： 又：v2＝v02+v12 所以：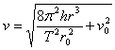

考点：

考点名称：万有引力定律的其他应用

万有引力定律的其他应用：

万有引力定律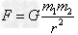：（G=6.67×10^-11N·m²/kg²），万有引力定律在天文学中的应用：
1、计算天体的质量和密度；
2、人造地球卫星、地球同步卫星、近地卫星；
3、发现未知天体；
4、分析重力加速度g随离地面高度h的变化情况；
①物体的重力随地面高度h的变化情况：物体的重力近似地球对物体的吸引力，即近似等于，可见物体的重力随h的增大而减小，由G=mg得g随h的增大而减小。
②在地球表面（忽略地球自转影响）：（g为地球表面重力加速度，r为地球半径）。
③当物体位于地面以下时，所受重力也比地面要小，物体越接近地心，重力越小，物体在地心时，其重力为零。
5、双星问题：天文学上把两颗相距比较近，又与其他星体距离比较远的星体叫做双星。双星的间距是一定的，它们绕二者连线上的同一点分别做圆周运动，角速度相等。以下图为例


由以上各式解得：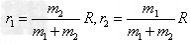
6、黄金代换公式：GM=gR²。

考点名称：运动的合成与分解

定义：
物体的实际运动往往是由几个独立的分运动合成的，由已知的分运动求跟它们等效的合运动叫做运动的合成；由已知的合运动求跟它等效的分运动叫做运动的分解。

运动的合成与分解基本关系：
①分运动的独立性；
②运动的等效性（合运动和分运动是等效替代关系，不能并存）；
③运动的等时性；
④运动的矢量性（加速度、速度、位移都是矢量，其合成和分解遵循平行四边形定则）。

互成角度的两个分运动的合运动的判断:
合运动的情况取决于两分运动的速度的合速度与两分运动的加速度的合加速度，两者是否在同一直线上，在同一直线上作直线运动，不在同一直线上将作曲线运动。
①两个直线运动的合运动仍然是匀速直线运动；
②一个匀速直线运动和一个匀加速直线运动的合运动是曲线运动；
③两个初速度为零的匀加速直线运动的合运动仍然是匀加速直线运动；
④两个初速度不为零的匀加速直线运动的合运动可能是直线运动也可能是曲线运动。当两个分运动的初速度的合速度的方向与这两个分运动的合加速度方向在同一直线上时，合运动是匀加速直线运动，否则是曲线运动。

怎样确定合运动和分运动:
①合运动一定是物体的实际运动；
②如果选择运动的物体作为参照物，则参照物的运动和物体相对参照物的运动是分运动，物体相对地面的运动是合运动。
③进行运动的分解时，在遵循平行四边形定则的前提下，类似力的分解，要按照实际效果进行分解。例如绳端速度的分解，通常有两个原则：按效果正交分解物体运动的实际速度，沿绳方向一个分量，另一个分量垂直于绳（效果：沿绳方向的收缩速度，垂直于绳方向的转动速度）。

小船渡河问题:

小船渡河是典型的运动合成的问题。一条宽度为L的河流，水流速度为V_s，已知船在静水中的速度为V_c，那么：
①渡河时间最短：
如图甲所示，设船上头斜向上游与河岸成任意角θ，这时船速在垂直于河岸方向的速度分量V₁=V_csinθ，渡河所需时间为：。
可以看出：L、V_c一定时，t随sinθ增大而减小；当θ=90°时，sinθ=1，所以，当船头与河岸垂直时，渡河时间最短，。

②V_c>V_s，渡河路径最短：
如图乙所示，渡河的最小位移即河的宽度。为了使渡河位移等于L，必须使船的合速度V的方向与河岸垂直。这是船头应指向河的上游，并与河岸成一定的角度θ。根据三角函数关系有：Vccosθ─V_s=0。
所以θ=arccos，因为0≤cosθ≤1，所以只有在V_c>V_s时，船才有可能垂直于河岸横渡。
③V_c＜V_s，渡河路径最短：
如果水流速度大于船上在静水中的航行速度，则不论船的航向如何，总是被水冲向下游。怎样才能使漂下的距离最短呢？如图丙所示，设船头V_c与河岸成θ角，合速度V与河岸成α角。可以看出：α角越大，船漂下的距离x越短，那么，在什么条件下α角最大呢？以V_s的矢尖为圆心，以V_c为半径画圆，当V与圆相切时，α角最大，根据cosθ=，船头与河岸的夹角应为：θ=arccos。
船漂的最短距离为：。
此时渡河的最短位移为：。

本文标题：好奇号火星探测器着陆-1966年 “金星”3号着陆
本文地址： http://www.61k.com/1094207.html