一 : 《如果，宅》241-60，如果宅2
41
当然台服妹子挺多的，问题是交流起来十分费劲。
比如还真有人听不懂老大的普通话。
老大为了追求一个上海MM，先是学习了几天上海话，无果之后又学习了几天英语。
爱情的力量。成果喜人。
“有啊逼有他扶。”老大说。“歪哟逼有他扶。”
42
当然这段感情还是走向了毁灭。
老大明白，感情是不能靠突击来取巧的。
当天晚上，老大毅然决然的删除了硬盘里几个论坛收集来的日本A片。
“重新做人。”老大说。
第二天，老大开始在各大论坛的北美区寻找“情景口语教材”。
不少人都以为老大要进军欧服，纷纷大喊老大英明。
而老大也在公会论坛贴出自己844分的国家英语六级证（满分750）说明自己的英语功底。
43
当然老大还是继续从国服向鬼雾峰调兵遣将未果。
我仔细的看了看老大的帖子。
“大家去那边的鬼服玩！”老大说。
群众普遍反映，“既然去台服了为什么不找个大服务器非要去找个鬼服？”
44
先行者总是伴随着痛苦与磨难。
我看BO玩的时候，看到有人喊“闭幕式！下副本！”
我琢磨着这2008都过去这么久了怎么还有人念念不忘。
只见BO从容的上着牧师号回答道：“行，走！”
“你是闭幕式？为啥叫你闭幕式？”我很奇怪的问。
“以前玩的不好。”BO很谦虚的说：“大家都叫我逼牧师。”
45
纳新是很辛苦的。
尤其是一个没有基础的服务器。
“本公会立足鬼雾峰已久，公会实力雄厚，每周三举行大规模PVP活动，每周四举行大规模PVE活动，现招募有志青年加入，共创美好明天！”
老大在服务器刷屏。
46
事实证明，老大被禁言了十几次还是有成效的。
竟然有5个人忍不住诱惑加入了《百人众》。
“有前途。”老大立刻把他们提拔到了副会长的级别。
几个人眼前放光仿佛已然盛世。
他们纷纷议论着这个拥有1个会长3个会长助理4个副会长的公会是个多么庞大的机构。
当然，他们完全没想到第一张《百人众》干部截图留念就等同于全家福了。
47
星期三晚上，公会组织了第一次大规模PVP活动。
当然，另一种说法叫做“竞技场5V5便当赛十场”。
星期四晚上，公会意欲组织大规模PVE活动剑指俄特加德要塞。
后因经济和人数原因（BO请假，只剩下了老大一人）临时变成了斯坦索姆带小号的活动。
48
来的新人退会了。
临走的时候为了报复老大，给老大的QQ好有印象瞎写一气。
那段时间不是很流行么？
“孩子我打掉了……”
“孩子我舍不得打掉……”
“孩子应该留下么……”
于是他们也打算这么做。
49
显然这些人小儿科了。
当时老大的好友印象就一句话。
“您的充气娃娃（注：男版）已经到货，请您查收。”
50
老大已经快要彻底放弃人生了。
本来老大以为上帝给了自己人生一个叫做《泪流满面》的游戏就够过分了；
没想到上帝最近又给老大的人生出了一个叫做《赶尽杀绝》的资料片。
51
说道这里我想起一个以前的故事。
我带着宝宝，伙同大屈、BO、洋子以及老大去KTV唱歌。
一进包间老大立刻轻车熟路的说“来几个小姐。”
所有人看着我不敢说话。
宝宝不轻不重的咳嗽了一声，老大回头不明所以的看着我们。
“哦，哦！哦！不用小姐了。”老大恍然大悟，对服务员说：“我们有了。”
这次所有人都看着宝宝，不敢说话。
52
其实公会成立初期，还是靠大屈的不懈努力拉来了几个妹子撑场面。
当时有件事闹的很大。
有个妹子在公会兴奋的说，大屈昨天向她求婚了。
当时老大一口茶水喷在了显示器上，立刻打了大屈的电话求实。
53
据说大屈这次玩台服感情玩的深沉了，对那姑娘说了一句话。
“我想对你进行合法的长期嫖娼。”
老大感慨道，大屈终于第二十六次找到了人生的真爱。
54
还是先说说副本进度吧。
老大作为一个T深知装备的重要，但是世代家传黑手终于展露了邪恶本性。
老大光荣的成为了布甲之友，腿甲之友；6个CD就没见过副本出板甲。
每次都是开尸体，下游戏，下QQ，下UT。
55
继续组织副本。
老大负责集合人，UT里自言自语着：“大屈怎么还不来？”
“一个联盟”听了插嘴问道：“你姘头怎么了，老大？”
“不知道，迟到10分钟了。”老大心神不安。
过了20秒。
“姘头？”
56
一个联盟是个术士，老大以前的职业，外号梁朝伟。
老大和他是在战场上认识的。
本来老大还琢磨这小子玩的是部落为啥要叫这个名字。但是进了战场在明白过来。
“一个联盟突袭了铁匠铺！”
“一个联盟突袭了伐木场！”
这些很具有误导性的战场提示经常让对方联盟阵脚大乱。
老大赞叹他的才华。
“算什么，我还认识一个叫‘你猜猜是谁’的盗贼呢。”一个联盟谦虚的说。
57
歌神考研之后还是打算来台服的。
“国服都被圣斗士和非主流占据了。”歌神说这句话的时候是八月份。
国服最恐怖的那段日子，各种诡异天赋横行的年代。
其实老大也深有感触。
曾经老大在百度知道问：“请问战士的PK天赋应该怎么选择？”
最佳答案：“惩戒。”
58
后来歌神带了几个小学妹来玩游戏。
各种非主流照片开始充斥公会论坛，都是大眼，粉腮，嘟嘴，剪刀手。
BO很不屑的说，嘟嘴，嘟个蛋。
“你看你这粗俗的。人家照相图的就是开心。”老大善意的批评道，然后端详着照片展露自己渊博的医学常识：“嘴勃起和J8勃起一样，都是人兴奋的表现。”
59
老大在台服经历了11个CD后终于在某个副本中第一次靠自己刷出了一把武器。
当时才是第二个BOSS，但是老大立刻退队，炉石回了达拉然。
只见老大器宇轩昂的脱下腿上的布甲，将披风调成显示后随风轻轻舞动，并且取消了头盔显示，背着紫色的武器在门口来来回回跑动。
“操你大爷，后面的不打了？赶紧回来！”BO很奇怪的问。
“装逼中，勿扰。”老大的自动回复
60
很多东西不亲自经历是写不出来的。
所以我打算一旦台服解锁就去鬼雾峰。
老大听了以后大喜。“洗干净了赶紧过来！”
这是老大的口头禅。但是，台服的不利言论也很风行。
“老大果然喜欢菊花。”群众议论纷纷。“每次来人都说让人家洗干净了等他。”
老大很苦恼，徒劳解释说自己只是一个“爱卫生的好少年”而已。
洋子在大洋彼岸出谋划策，说“你爱干净可以，但是你能换个口头禅吗？”
于是这次我再去的时候，老大说：“刷了牙赶紧过来！”
“老大原来好这口。”群众继续议论纷纷。
所以说，和以前一样，群众还是最操蛋的。
二 : 如果复数2
如果复数
|
=
由
故选C． |
考点：
考点名称：复数的概念及几何意义复数的概念：
形如a+bi（a，b∈R）的数叫复数，其中i叫做虚数单位。全体复数所成的集合叫做复数集，用字母C表示。
复数的表示：
复数通常用字母z表示，即z=a+bi（a，b∈R），这一表示形式叫做复数的代数形式，其中a叫复数的实部，b叫复数的虚部。
复数的几何意义：
（1）复平面、实轴、虚轴：
点Z的横坐标是a，纵坐标是b，复数z=a+bi（a、b∈R）可用点Z（a，b）表示，这个建立了直角坐标系来表示复数的平面叫做复平面，x轴叫做实轴，y轴叫做虚轴。显然，实轴上的点都表示实数，除原点外，虚轴上的点都表示纯虚数
（2）复数的几何意义：复数集C和复平面内所有的点所成的集合是一一对应关系，即
这是因为，每一个复数有复平面内惟一的一个点和它对应；反过来，复平面内的每一个点，有惟一的一个复数和它对应。
这就是复数的一种几何意义，也就是复数的另一种表示方法，即几何表示方法。
复数的模：
复数z=a+bi（a、b∈R）在复平面上对应的点Z（a，b）到原点的距离叫复数的模，记为|Z|，即|Z|=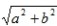
虚数单位i：
（1）它的平方等于-1，即i2=-1；
（2）实数可以与它进行四则运算，进行四则运算时，原有加、乘运算律仍然成立
（3）i与-1的关系：i就是-1的一个平方根，即方程x2=-1的一个根，方程x2=－1的另一个根是-i。
（4）i的周期性：i4n+1=i，i4n+2=-1，i4n+3=-i，i4n=1。
复数模的性质：
复数与实数、虚数、纯虚数及0的关系：
对于复数a+bi（a、b∈R），当且仅当b=0时，复数a+bi（a、b∈R）是实数a；当b≠0时，复数z=a+bi叫做虚数；当a=0且b≠0时，z=bi叫做纯虚数；当且仅当a=b=0时，z就是实数0。
复数集与其它数集之间的关系：
。
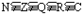复数的运算：
1、复数z1与z2的和的定义：z1+z2=（a+bi）+（c+di）=（a+c）+（b+d）i；
2、复数z1与z2的差的定义：z1-z2=（a+bi）-（c+di）=（a-c）+（b-d）i；
3、复数的乘法运算规则：设z1=a+bi，z2=c+di（a、b、c、d∈R）是任意两个复数，那么它们的积（a+bi）（c+di）=（ac-bd）+（bc+ad）i，其实就是把两个复数相乘，类似两个多项式相乘，在所得的结果中把i2换成-1，并且把实部与虚部分别合并，两个复数的积仍然是一个复数。
4、复数的除法运算规则：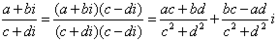
。
复数加法的几何意义：
设
为邻边画平行四边形
就是复数
对应的向量。
，则这两个复数的差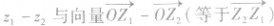
对应，这就是复数减法的几何意义。
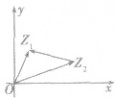共轭复数：当两个复数的实部相等，虚部互为相反数时，这两个复数叫做互为共轭复数。
虚部不等于0的两个共轭复数也叫做共轭虚数。
复数z=a+bi和
=a-bi（a、b∈R）互为共轭复数。
复数的运算律：
1、复数的加法运算满足交换律：z1+z2=z2+z1；
结合律：（z1+z2）+z3=z1+（z2+z3）；
2、减法同加法一样满足交换律、结合律。
3、乘法运算律：（1）z1（z2z3）=（z1z2）z3；（2）z1（z2+z3）=z1z2+z1z3；（3）z1（z2+z3）=z1z2+z1z3
共轭复数的性质：
本文标题：如果宅2-《如果，宅》241-60，如果宅2 61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1