一 : 初中数学反比例函数知识点

初中数学反比例函数知识点
利用反比例关系,y=k/x,其中x属于自变量,y属于因变量,y与x成反比例关系,k一定,

二 : 反比例函数知识点归纳和典型例题
反比例函数知识点归纳和典型例题
知识点归纳
(一)反比例函数的概念
1.
()可以写成()的形式,注意自变量x的指数为,
在解决有关自变量指数问题时应特别注意系数
2.
(这一限制条件; )也可以写成xy=k的形式,用它可以迅速地求出反比例函数解
析式中的k,从而得到反比例函数的解析式;
3.反比例函数的自变量
(二)反比例函数的图象 ,故函数图象与x轴、y轴无交点.
在用描点法画反比例函数的图象时,应注意自变量x的取值不能为0,且x应对称取点(关于原点对称).
(三)反比例函数及其图象的性质
1.函数解析式:(
) 2.自变量的取值范围:
3.图象:
(1)图象的形状:双曲线.
越大,图象的弯曲度越小,曲线越平直.
越小,图象的弯曲度越大.
(2)图象的位置和性质:
与坐标轴没有交点,称两条坐标轴是双曲线的渐近线.
当时,图象的两支分别位于一、三象限;
在每个象限内,y随x的增大而减小;
当时,图象的两支分别位于二、四象限;
在每个象限内,y随x的增大而增大.
(3)对称性:图象关于原点对称,即若(a,b)在双曲线的一支上,
则(
,)在双曲线的另一支上. 1





图象关于直线
则(,)和(
4.k的几何意义 对称,即若(a,b)在双曲线的一支上, ,)在双曲线的另一支上.
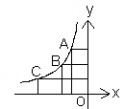
如图1,设点P(a,b)是双曲线
PB⊥y轴于B点,则矩形PBOA的面积是上任意一点,作PA⊥x轴于A点,(三角形PAO和三角形PBO的面积都是).
如图2,由双曲线的对称性可知,P关于原点的对称
点Q也在双曲线上,作QC⊥PA的延长线于C,则有三
角形PQC的面积为.
图1 图2
5.说明:
(1)双曲线的两个分支是断开的,研究反比例函数的增减性时,要将两个分支分别讨论,不能一概而论.
(2)直线
系:
时,两图象没有
当
必有两个交点,
原点成中心对称.
与双曲线 当交点; 时,两图象且这两个交点关于的关
2



(四)充分利用数形结合的思想解决问题.
例题分析
1.反比例函数的概念
(1)下列函数中,y是x的反比例函数的是( ).
A.y=3x B. C.3xy=1 D.
(2)下列函数中,y是x的反比例函数的是( ).
A.
B. C. D. 2.图象和性质
(1)已知函数是反比例函数,
①若它的图象在第二、四象限内,那么k=_________ ②若y随x的增大而减小,那么k=___________.
(2)已知一次函数y=ax+b的图象经过第一、二、四象限,则函数
象位于第________象限. 的图
(3)若反比例函数经过点(
经过第_____象限. ,2),则一次函数的图象一定不
(4)已知a·b<0,点P(a,b)在反比例函数的图象上,
则直线不经过的象限是( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
(5)若P(2,2)和Q(m,)是反比例函数图象上的两点, 则一次函数y=kx+m的图象经过( ).
A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限
(6)已知函数
( ). 和(k≠0),它们在同一坐标系内的图象大致是
3



A. B.
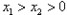
C.
D.


3.函数的增减性
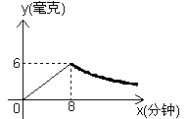
(1)在反比例函数的图象上有两点
,,且
,则的值为( ).
A.正数 B.负数 C.非正数 D.非负数
(2)在函数
,则函数值
A.
C.<<<<(a为常数)的图象上有三个点、、的大小关系是( ). <<<< ,, B. D.
(3)下列四个函数中:①;②;③;④. y随x的增大而减小的函数有( ).
A.0个 B.1个 C.2个 D.3个
(4)已知反比例函数的图象与直线y=2x和y=x+1的图象过同一点,则当x>0时,这个反比例函数的函数值y随x的增大而______ (填“增大”或“减小”).
4.解析式的确定
(1)若与成反比例,与成正比例,则y是z的( ).
A.正比例函数 B.反比例函数 C.一次函数 D.不能确定
(2)若正比例函数y=2x与反比例函数
4

的图象有一个交点为 (2,m),则
m=_____,k=________,它们的另一个交点为________.
(3)已知反比例函数的图象经过点
第二、四象限,求的值. ,反比例函数的图象在
(4)已知一次函数y=x+m与反比例函数()的图象在第一象限内的交点为P (x0,3).
①求x0的值;②求一次函数和反比例函数的解析式.
5.面积计算
(1)如图,在函数的图象上有三个点A、B、C,过这三个点分别向x轴、
、y轴作垂线,过每一点所作的两条垂线段与x轴、y轴围成的矩形的面积分别为
、,则( ).
B. C. D. A.
第(1)题图 第(2)题图
(2)如图,A、B是函数的图象上关于原点O对称的任意两点,AC//y轴,BC//x轴,△ABC的面积S,则( ).
A.S=1 B.1<S<2 C.S=2 D.S>2
(3)如图,Rt△AOB的顶点A在双曲线上,且S△AOB=3,求m的值. 5

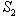
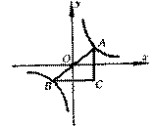
第(3)题图 第(4)题图
(4)已知函数的图象和两条直线y=x,y=2x在第一象限内分别相交于P1和P2两点,过P1分别作x轴、y轴的垂线P1Q1,P1R1,垂足分别为Q1,R1,过P2分别作x轴、y轴的垂线P2 Q 2,P2 R 2,垂足分别为Q 2,R 2,求矩形O Q 1P1 R 1和O Q 2P2 R 2的周长,并比较它们的大小.
(5)如图,正比例函数y=kx(k>0)和反比例函数的图象相交于A、C两点,过A作x轴垂线交x轴于B,连接BC,若△ABC面积为S,则S=_________. 第(5)题图 第(6)题图
(6)如图在Rt△ABO中,顶点A是双曲线与直线在第四象限的交点,AB⊥x轴于B且S△ABO=.
①求这两个函数的解析式;
②求直线与双曲线的两个交点A、C的坐标和△AOC的面积.
6




(7)如图,已知正方形OABC的面积为9,点O为坐标原点,点A、C分别在x轴、y轴上,点B在函数(k>0,x>0)的图象上,点P (m,n)是函数
(k>0,x>0)的图象上任意一点,过P分别作x轴、y轴的垂线,垂足为E、F,设矩形OEPF在正方形OABC以外的部分的面积为S.
① 求B点坐标和k的值;
② 当时,求点P的坐标;
③ 写出S关于m的函数关系式.
7
6
.综合应用
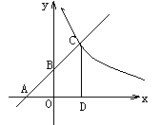

(1)若函数y=k1x(k1≠0)和函数(k2
≠0)在同一坐标系内的图象没有公共点,则k1
k2( ).
A.互为倒数 B.符号相同 C.绝对值相等
D.符号相反
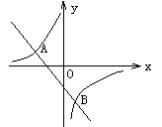
(2)如图,一次函数的图象与反比例和 数
的图象交于A、B两点:A(,1),B(1,n).
① 求反比例函数和一次函数的解析式;
② 根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.
(3)如图所示,已知一次函数(k≠0)的图象
与x 轴、y轴分别交于A、B两点,且与反比例函数(m≠0)的图象在第一象限交于C点,CD垂直于x轴,垂足为D,若OA=OB=OD=1.
① 求点A、B、D的坐标;
② 求一次函数和反比例函数的解析式.
8


(4)如图,一次函数的图象与反比例函数的图象交于第一象限C、D两点,坐标轴交于A、B两点,连结OC,OD(O是坐标原点).
① 利用图中条件,求反比例函数的解析式和m的值;
② 双曲线上是否存在一点P,使得△POC和△POD的面积相等?若存在,给出证明并求出点P的坐标;若不存在,说明理由.
(5)不解方程,判断下列方程解的个数.
①
; ②.
9
三 : 反比例函数知识点及复习题
反比例函数精讲精练
一、反比例函数的概念:
知识要点:
1、一般地,形如 y = k ( k是常数, k = 0 ) 的函数叫做反比例函数。 x
注意:(1)常数 k 称为比例系数,k 是非零常数;
(2)解析式有三种常见的表达形式:
(A)y = k-1(k ≠ 0) (B)xy = k(k ≠ 0) (C)y=kx(k≠0) x
x1111③y?2 ④.y??⑤y??⑥y? ;其中xx?12x3x2例题讲解:有关反比例函数的解析式 例1、(1)下列函数,① x(y?2)?1②. y?
是y关于x的反比例函数的有:_________________。
(2)函数y?(a?2)xa2?2是反比例函数,则a的值是( )
A.-1 B.-2 C.2 D.2或-2
(3)如果y是m的反比例函数,m是x的反比例函数,那么y是x的( )
A.反比例函数 B.正比例函数 C.一次函数 D.反比例或正比例函数
练习:(1)如果y是m的正比例函数,m是x的反比例函数,那么y是x的( )
(2)如果y是m的正比例函数,m是x的正比例函数,那么y是x的( )
(4)反比例函数y?k的图象经过(—2,5
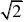
, n), (k?0)x
求(1)n的值; (2)判断点B(4
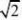
2,
(5)已知函数y?y1?y2,其中y1与x成正比例, y2与x成反比例,且当x=1时,y=1;x=3时,y=5. 求:(1)求y关于x的函数解析式; (2)当x=2时,y的值.
二、反比例函数的图象和性质:
知识要点:
1、形状:图象是双曲线。
2、位置:(1)当k>0时,双曲线分别位于第________象限内;(2)当k<0时, 双曲线分别位于第________象限内。
3、增减性:(1)当k>0时,_________________,y随x的增大而________;
(2)当k<0时,_________________,y随x的增大而______。
4、变化趋势:双曲线无限接近于x、y轴,但永远不会与坐标轴相交
5、对称性:(1)对于双曲线本身来说,它的两个分支关于直角坐标系原点____________;
(2)对于k取互为相反数的两个反比例函数(如:y = 例题讲解:
6?6
和y = )来说,它们是关于x轴,y轴___________。 xx
(一)反比例函数的图象和性质:
例2、(1)写出一个反比例函数,使它的图象经过第二、四象限 .
m
y?(2m?1)x(2)若反比例函数
2
?2
的图象在第二、四象限,则m的值是( )
1
的任意实数; C、-1; D、不能确定 2
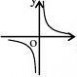
k
(3)已知k?0,函数y?kx?k和函数y?在同一坐标系内的图象大致是( )
x
A、 -1或1; B、小于
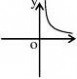
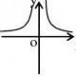


x
x
x
x
x2
(4)正比例函数y

?和反比例函数y?的图象有

个交点.
2x
k
(5)正比例函数y??
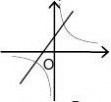
5x的图象与反比例函数y?(k?0)的图象相交于点A(1,a),
x
则a= .
例3、(1)下列函数中,当x?0时,y随x的增大而增大的是( ) A.y??3x?4 B.y??x?2 C.y??(2)已知反比例函数y?
1
314
D.y?.
2xx
?2
的图象上有两点A(x1,y1),B(x2,y2),且x1?x2, x
则y1?y2的值是( )
A.正数 B.负数 C.非正数 D.不能确定 (3)若点(x1,y1)、(x2,y2)和(x3,y3)分别在反比例函数y??则下列判断中正确的是( )
A.y1?y2?y3 B.y3?y1?y2 C.y2?y3?y1 D.y3?y2?y1 (4)在反比例函数y?
2
的图象上,且x1?x2?0?x3,x
k?1
的图象上有两点(x1,y1)和(x2,y2),若x时,y0?x1?21?y2,则k的取x
值范围是 .
k2
(k2≠0)的一个交点为(m,n),则另一个交点为_________. x
(6)老师给出一个函数,甲、乙、丙三位同学分别指出了这个函数的一个性质:
甲:函数的图象经过第二象限; 乙:函数的图象经过第四象限; 丙:在每个象限内,y随x的增大而增大. 请你根据他们的叙述构造满足上述性质的一个函数: . (二)反比例函数与三角形面积结合题型。
2
例4、(1)矩形的面积为6cm,那么它的长y(cm)与宽x(cm)之间的函数关系用图象表示为( )
(5)正比例函数y=k1x(k1≠0)和反比例函数y=
A
B
C
D
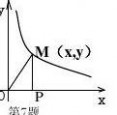
k(k>0)在第一象限内的图象如图,点M(x,y)是图象上一点,MP垂直x轴于点P, x
MQ垂直y轴于点Q;① 如果矩形OPMQ的面积为2,则k=_________;
② 如果△MOP的面积=____________.
(2)反比例函数y=
总结:(1) 点 M(x,y) 是双曲线上任意一点,则矩形OPMQ的面积是
M P *M Q = ︳x︱︳y︱= ︳xy︱
111 (2) M P= ︳x︱, O P= ︳y︱ ;S△MPO=MP* OP=︳x︱︳y︱ =︳xy︱ 222
k (3)老师在同一个直角坐标系中画了一个反比例函数y?(k?0)的图象以及正比例函数x
y??2x的图象,请同学观察有什么特点。甲同学说:双曲线与直线y??2x有两个交点;乙同学说:双曲线上任意一点到两坐标轴的距离的积都是5.请你根据甲、乙两位同学的说法,写出这个反比例函数的解析式 . (4) 如图,正比例函数y?kx(k?0)与反比例函数y?2的图象相交于A、C
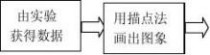


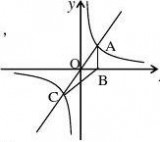
x过点A作AB
⊥x轴于点B,连结BC.则ΔABC的面积等于( )
A.1 B.2 C.
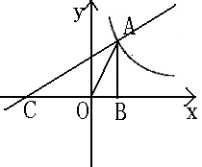
4 D.随k的取值改变而改变. k与直线y??x?m x
3?在第二象限的交点,AB垂直x轴于B,且S△ABO=, 2 (5) 如图,RtΔABO的顶点A是双曲线y?
则反比例函数的解析式 .
(6) 如图,在平面直角坐标系中,直线y?x?kk与双曲线y?在第一象限交于点A, x2
(第(5)题) 与x轴交于点C,AB⊥x轴,垂足为B,且S?AOB=1.求:
(1)求两个函数解析式; (2)求△ABC的面积.
三、反比例函数的应用:
1、用反比例函数来解决实际问题的步骤:
例题讲解:
例5、一辆汽车往返于甲、乙两地之间,如果汽车以50千米/时的平均速度从甲地出发,则6小时可到达乙地.
(1)写出时间t (时)关于速度v(千米/时)的函数关系式,说明比例系数的实际意义.
(2)因故这辆汽车需在5小时内从甲地到乙地,则此时汽车的平均速度至少应是多少?
例6、你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:拉面师傅在一定体积的面团的条件下制做拉面,通过一次又一次地拉长面条,测出每一次拉长面条后面条的总长度与面条的粗细(橫截面积)
(1)请根据右表中的数据求出面条的总长度y(m)与面条的粗细(橫截面积) s(mm)函数关系式; 2
(2)求当面条粗1.6mm时,面条的总长度是多少?

2
本文标题:反比例函数知识点-初中数学反比例函数知识点61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1