一 : 方阵问题

方阵问题——基础学习



一. 解答题



2、实心方阵例1：30人一排的方阵，求最外层有多少人？

【答案】116人。

【解题关键点】利用公式四周人(或物)数=[每边人(或物)数-1]×4，（30-1）×4=116（人）

【结束】

3、实心方阵例2：20人一排的方阵共有多少人？

【答案】400（人）。

【解题关键点】利用公式：实方阵总人(或物)数=每边人(或物)数×每边人(或物)数，20×20=400（人）。

【结束】



5、空心方阵例1：小华用围棋摆了一个六层的空心方阵,共用264颗棋子,问最里层有多少个棋子？( )

A 36 B 24 C 30 D 22

【答案】B

【解题关键点】

法一：对于空心方阵，最外层每边数=总数÷4÷层数+层数

最外层每边数=（264÷4÷6）+6=17人；

共六层，最外一层与最里一层相差5层。

每层每边数差两个，所以最里层每边数=17-5×2=7个

那么最里层个数是4×7-4=24个。

法二：方阵每层相差8个。那么从里向外数，第二层比第一层多8个，第三比第一层多16个，第四层比第一层多24个，第五层比第一层多32个，第六层比第一层多40个；

那么最里一层就是（264-8-16-24-32-40）÷6=24个

【结束】

6、空心方阵例2：一个两层空心方阵最外层有16人，一共多少人？（）

A.16 B.24 C.10 D.22

【答案】B

【解题关键点】最外层16人-四个角4人=12人

12÷4=3，即每个边3人

内层每个边应该比外层少2人以占角拐弯，故每个边仅1人，加上4个角，内层共8人

综上，内外两层共24人

总而言之，就是外层每排5人，内层每排3人，最中间空出一个人位置的两层空心方阵。

【结束】

7、方阵综合例1：

方阵外一层总人数比内一层的总人数多8

每边人数与该层人数关系是：最外层总人数＝（边人数－1）×4

方阵总人数＝最外层每边人数的平方

空心方阵的总人(或物)数=（最外层每边人(或物)数－空心方阵的层数）×空心方阵的层数×4

去掉一行、一列的总人数=去掉的每边人数×2-1

【例1】某校的学生刚好排成一个方阵，最外层的人数是96人，问这个学校共有学生？

【答案】625

【解题关键点】解答：最外层每边的人数是96÷4+1＝25，刚共有学生25×25=625

【结束】

8、方阵综合例2：五年级学生分成两队参加学校广播操比赛，他们排成甲乙两个方阵，其中甲方阵每边的人数等于8，如果两队合并，可以另排成一个空心的丙方阵，丙方阵每边的人数比乙方阵每边的人数多4人，甲方阵的人数正好填满丙方阵的空心。五年级参加广播操比赛的一共有多少人? （）

A160 B 204 C 100 D 260

【答案】D

【解题关键点】设乙最外边每人数为Y，则丙为Y+4.

8×8+Y×Y+8×8=(Y+4)(Y+4)， 求出Y=14,则共有人数：14×14+8×8＝260。

【结束】

9、方阵综合例3：明明用围棋子摆成一个三层空心方阵，如果最外层每边有围棋子15个，明明摆这个方阵最里层一周共有多少棋子？摆这个三层空心方阵共用了多少个棋子?

【答案】56个，144个。

【解题关键点】最外层有(15-1)×4=56个。则里二层为56-8×2=40 ，应用公式，用棋子（15－3）×3×4＝144。

【结束】

10、方阵综合例4：学校运动会上，晨光小学组成一个大型方阵队，方阵队最外层每边25人，共8层；中间部分是15名同学组成的运动会会徽，这个方阵共有多少名同学？

【答案】

【解题关键点】空心方阵问题总数的公式是：总数=(最外层每边数-层数)*层数*4

【结束】

11、方阵综合例5：108人排成空心方阵，如果最外层每边12人，那么共有几层？

【答案】3（层）。

【解题关键点】可以把相邻两层每边人数想成是一个等差数列，公差是2（方阵问题中有这样一个知识点，就是相邻两边每边人数相差2）。

通过“12×12-108=36 ”计算我们知道了此方阵是中间去掉了6×6的空心方阵，那么从每边12人排到每边6人，通过等差数列求项数《公式是：项数=（末项-首项）÷(公差+1）》的计算我们能求出（12-6）÷2+1=4（层），应该是有4层，

还因为我们已经知道要去掉的是每边6人那一层，所以刚才的算式就不用加1了，结果就是“（12-6）÷2=3（层）”。

【结束】

11、方阵综合例6：国庆阅兵大典，参演学生组成一个方阵，已知方阵由外到内第二层有120人，则该方阵共有学生多少人？（ ）

A．625 B．841 C．1024 D．1089

【答案】D

【解题关键点】方阵由外到内第二层有120人，那么最外层有120+8=128人，那么每边有（128+4）÷4=33人，则整个方阵有33×33=1089人。

【结束】

12、方阵综合例7：某校的学生刚好排成一个方阵，最外层的人数是96人，问这个学校共有学生（ ）。

A．600人 B．615人 C．625人 D．640人

【答案】C

【解题关键点】根据方阵问题的基本公式，可知学校共有学生=方阵总人数=（96÷4+1）　　=625。

【结束】

13、方阵综合例8：某校参加军训队列表演比赛，组织一个方阵队伍。如果每班60人，这个方阵至少要有4个班的同学参加，如果每班70人，这个方阵至少要有3个班的同学参加。那么组成这个方阵的人数应该为几人？ （ ）

A．169 B．196 C．225 D．256

【答案】B

【解题关键点】依题意知道方阵数大于180小于210，考虑到方阵人数必须是一个平方数因此只能是196人成一个14×14的方阵。

【结束】

二 : 方阵问题

方阵问题——基础学习



一. 解答题



2、实心方阵例1：30人一排的方阵，求最外层有多少人？

【答案】116人。

【解题关键点】利用公式四周人(或物)数=[每边人(或物)数-1]×4，（30-1）×4=116（人）

【结束】

3、实心方阵例2：20人一排的方阵共有多少人？

【答案】400（人）。

【解题关键点】利用公式：实方阵总人(或物)数=每边人(或物)数×每边人(或物)数，20×20=400（人）。

【结束】



5、空心方阵例1：小华用围棋摆了一个六层的空心方阵,共用264颗棋子,问最里层有多少个棋子？( )

A 36 B 24 C 30 D 22

【答案】B

【解题关键点】

法一：对于空心方阵，最外层每边数=总数÷4÷层数+层数

最外层每边数=（264÷4÷6）+6=17人；

共六层，最外一层与最里一层相差5层。

每层每边数差两个，所以最里层每边数=17-5×2=7个

那么最里层个数是4×7-4=24个。

法二：方阵每层相差8个。那么从里向外数，第二层比第一层多8个，第三比第一层多16个，第四层比第一层多24个，第五层比第一层多32个，第六层比第一层多40个；

那么最里一层就是（264-8-16-24-32-40）÷6=24个

【结束】

6、空心方阵例2：一个两层空心方阵最外层有16人，一共多少人？（）

A.16 B.24 C.10 D.22

【答案】B

【解题关键点】最外层16人-四个角4人=12人

12÷4=3，即每个边3人

内层每个边应该比外层少2人以占角拐弯，故每个边仅1人，加上4个角，内层共8人

综上，内外两层共24人

总而言之，就是外层每排5人，内层每排3人，最中间空出一个人位置的两层空心方阵。

【结束】

7、方阵综合例1：

方阵外一层总人数比内一层的总人数多8

每边人数与该层人数关系是：最外层总人数＝（边人数－1）×4

方阵总人数＝最外层每边人数的平方

空心方阵的总人(或物)数=（最外层每边人(或物)数－空心方阵的层数）×空心方阵的层数×4

去掉一行、一列的总人数=去掉的每边人数×2-1

【例1】某校的学生刚好排成一个方阵，最外层的人数是96人，问这个学校共有学生？

【答案】625

【解题关键点】解答：最外层每边的人数是96÷4+1＝25，刚共有学生25×25=625

【结束】

8、方阵综合例2：五年级学生分成两队参加学校广播操比赛，他们排成甲乙两个方阵，其中甲方阵每边的人数等于8，如果两队合并，可以另排成一个空心的丙方阵，丙方阵每边的人数比乙方阵每边的人数多4人，甲方阵的人数正好填满丙方阵的空心。五年级参加广播操比赛的一共有多少人? （）

A160 B 204 C 100 D 260

【答案】D

【解题关键点】设乙最外边每人数为Y，则丙为Y+4.

8×8+Y×Y+8×8=(Y+4)(Y+4)， 求出Y=14,则共有人数：14×14+8×8＝260。

【结束】

9、方阵综合例3：明明用围棋子摆成一个三层空心方阵，如果最外层每边有围棋子15个，明明摆这个方阵最里层一周共有多少棋子？摆这个三层空心方阵共用了多少个棋子?

【答案】56个，144个。

【解题关键点】最外层有(15-1)×4=56个。则里二层为56-8×2=40 ，应用公式，用棋子（15－3）×3×4＝144。

【结束】

10、方阵综合例4：学校运动会上，晨光小学组成一个大型方阵队，方阵队最外层每边25人，共8层；中间部分是15名同学组成的运动会会徽，这个方阵共有多少名同学？

【答案】

【解题关键点】空心方阵问题总数的公式是：总数=(最外层每边数-层数)*层数*4

【结束】

11、方阵综合例5：108人排成空心方阵，如果最外层每边12人，那么共有几层？

【答案】3（层）。

【解题关键点】可以把相邻两层每边人数想成是一个等差数列，公差是2（方阵问题中有这样一个知识点，就是相邻两边每边人数相差2）。

通过“12×12-108=36 ”计算我们知道了此方阵是中间去掉了6×6的空心方阵，那么从每边12人排到每边6人，通过等差数列求项数《公式是：项数=（末项-首项）÷(公差+1）》的计算我们能求出（12-6）÷2+1=4（层），应该是有4层，

还因为我们已经知道要去掉的是每边6人那一层，所以刚才的算式就不用加1了，结果就是“（12-6）÷2=3（层）”。

【结束】

11、方阵综合例6：国庆阅兵大典，参演学生组成一个方阵，已知方阵由外到内第二层有120人，则该方阵共有学生多少人？（ ）

A．625 B．841 C．1024 D．1089

【答案】D

【解题关键点】方阵由外到内第二层有120人，那么最外层有120+8=128人，那么每边有（128+4）÷4=33人，则整个方阵有33×33=1089人。

【结束】

12、方阵综合例7：某校的学生刚好排成一个方阵，最外层的人数是96人，问这个学校共有学生（ ）。

A．600人 B．615人 C．625人 D．640人

【答案】C

【解题关键点】根据方阵问题的基本公式，可知学校共有学生=方阵总人数=（96÷4+1）　　=625。

【结束】

13、方阵综合例8：某校参加军训队列表演比赛，组织一个方阵队伍。如果每班60人，这个方阵至少要有4个班的同学参加，如果每班70人，这个方阵至少要有3个班的同学参加。那么组成这个方阵的人数应该为几人？ （ ）

A．169 B．196 C．225 D．256

【答案】B

【解题关键点】依题意知道方阵数大于180小于210，考虑到方阵人数必须是一个平方数因此只能是196人成一个14×14的方阵。

【结束】

三 : 方阵问题

方阵其实是一种队形，一个团队排队,横着排叫行,竖着排叫列,若行数与列数都相等,正好排成一个正方形,这种队形就叫做方阵。将一些物体按照这样的方式排列起来，也叫做方阵。

方阵一般分为两类：实心方阵和空心方阵。其基本特点是：不论哪一层,每边上的人(或物)数量都相同；每向里一层,每条边上的人(或物)就少2，每一层的人(或物)的总数就少4。

1、方阵不论哪一层,每边上的人(或物)数量都相同,每向里一层,每边上的 人数就少2。
2、每边人(或物)数和四周人(或物)的关系;
四周人(或物)数=[每边人(或物)数-1]×4
每边人(或物)数=四周人(或物)数÷4+1
3、中实方阵的总人数(或物)=每边人(或物)数×每边人(或物)数
4、空心方阵的总人(或物)数=（最外层每边人(或物)数－空心方阵的层数）×空心方阵的层数×4
6、方阵外一层总人数比内一层的总人数多8
7、去掉一行、一列的总人数=去掉的每边人数*2-1

通过点子图理解方阵的特点及方阵问题中的四个数量关系

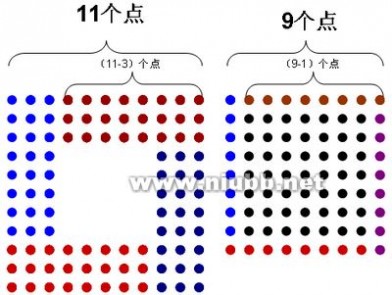
第一个空心方阵的总点数：（11-3）×3×4=56（点）；

第二个实心方阵外层点数：（9-1）×4=32（点

例题讲解

例1、某校的学生刚好排成一个方阵，最外层的人数是96人，问这个学校共有学生？

分析：要求出学校总人数，就要求出每边有多少人？

要求每边人数，利用已知，最外层的人数是96人，利用公式2，可以求出每边上的人数。

每边人数=96/4+1=25

公式3：中实方阵的总人数(或物)=每边人(或物)数×每边人(或物)数
25*25=625

例2、明明用围棋子摆成一个三层空心方阵，如果最外层每边有围棋子15个，明明摆这个方阵最里层一周共有多少棋子？摆这个三层空心方阵共用了多少个棋子?

第一问：可以用2种方法解答

第一种：利用公式1：方阵不论哪一层,每边上的人(或物)数量都相同,每向里一层,每边上的 人数就少2

最外层每边15个，里边一层每边（15-2），再往里一层每边（15-2-2）个

知道最里边每边有（15-2-2）个

利用公式2：四周人(或物)数=[每边人(或物)数-1]×4

（15-2-2-1）*4=40个

第二种方法：

利用公式2，求出最外一层四周有多少个：（15-1）*4=56个

利用公式6：方阵外一层总人数比内一层的总人数多8，56-8-8=40个

第二问：可以用2种方法解答

第一种：

最外边四周有几个：（15-1）*4=56

里边一层四周有几个：（15-2-1）*4=48

最里边一层有几个：（15-2-2-1）*4=40

共用：56+48+40=144

第二种

利用公式4：空心方阵的总人(或物)数=（最外层每边人(或物)数－空心方阵的层数）×空心方阵的层数×4
（15-3）*3*4=144

例3、军训的学生进行队列表演，排成了一个7行7列的正方形队列，如果去掉一行一列，要去掉多少人？还剩下多少人？

利用公式：去掉一行、一列的总人数=去掉的每边人数*2-1

例4、国庆节前夕，在街中心一塑像的周围，用204盆鲜花围成一个每边三成的方阵。求外面一层每边有鲜花多少盆？

因为：空心方阵的总花盆数=（最外层每边花盆数－空心方阵的层数）×空心方阵的层数×4。

这里的204盆鲜花也就是总盆数，现在由总盆数求外面一层每边花盆数。

先把总数平均分成4份，求图中四种颜色方块中，每种颜色方块里的鲜花有多少盆：204÷4=51（盆）；

再除以3层，求图中每种颜色方块里，每一行有鲜花多少盆：51÷3=17（盆）；

最后补加图中同一行另一种颜色的鲜花3盆，求外面一层每边有鲜花多少盆：17+3=20（盆）。

基本练习：

1、三年级一班参加运动会入场式,排成一个方阵,最外层一周的人数为20人,问方阵最外层每边的人数是多少?这个方阵共有多少人?

2、小明用围棋子摆了一个五层的空心方阵，共用了 200个棋子，问最外边一层每边有多少个棋子？

3、运动员入场式要求排成一个9行9列的正方形方阵，如果去掉2行2列，要减少多少运动员？

4、某校少先队员可以排成一个四层空心方阵如果最外层每边有20个学生,问这个空心方阵最里边一周有多少个学生?这个四层空心方阵共有多少个学生?

5、用121盆花摆一个方阵花坛，最外一层每边有多少盆花？最外层一共有多少盆花？

6、游行队伍中，手持鲜花的少先队员在一辆彩车的四周围成每边三层的方阵。最外层每边12人，问彩车周围的少先队员共有多少人？

本文标题：方阵问题-方阵问题
本文地址： http://www.61k.com/1082972.html