一 : 71重力式挡土墙设计

重力式挡土墙设计经验谈

【摘要】 对库仑、朗肯土压力理论和《建筑地基基础设计规范GBJ7-89》附录10—“挡土墙主动土压力系数Ka”提出一些看法，提出了粘性土主动土压力计算方法的改进；还提出了以抗滑移稳定为条件决定挡土墙截面的新方法和抗倾覆稳定验算的公式，并阐明墙身强度和地基应力的验算，举例说明一般重力式挡土墙的计算。

【关键词】 主动土压力 被动土压力 抗滑移稳定性 抗倾覆稳定性 0 引 言

在土建工程中，经常用挡土墙来支挡上下高差的土体，而重力式挡土墙是用得较多的一种形式。一般来讲，此种挡土墙的设计偏于保守的不少；但也有因考虑不周而致挡墙倒塌，甚至连地基发生整体滑动或因发生滑坡而被推倒。

一般重力式挡土墙的设计，须考虑以下五个问题：

(1)抗滑移稳定性；

(2)抗倾覆稳定性；

(3)墙身的强度；

(4)地基的应力；

(5)地基的整体稳定性。

关于墙身的强度，一般毋需验算，如有必要，仅验算最危险截面，即墙身和基础结合处的强度就可以了。如地基为抗剪强度较低的软土或基底下有软弱夹层时，除验算基底和下卧层的应力外，还需作地基稳定性验算。如因切割坡脚而砌筑挡墙，应加强工程地质勘察工作，特别注意山坡下是否存在容易发生滑坡的地质构造?经验算，切割坡脚后，有发生滑坡的可能，则此墙应作抗滑挡土墙考虑。

1 关于土压力问题

1.1 对库仑、朗肯土压理论的看法

法国学者(Coulomb)库仑在1773年提出的和英国的(Rankine)朗肯在1857年提出的两种土压力理论，直到现在，工程界还在普遍应用。这是因为这两种理论仍有其实用价值。第一，其计算模型比较简单，计算过程也不复杂；其二，用来计算主动土压力，误差不太大，而尤以库仑理论更小些。众所周知，无论库仑或朗肯理论都假定土为理想散体，只有摩擦力产生，而无粘聚力存在，故只适用于砂性土。关于散体的极限平衡理论，前苏联学者索科洛夫斯基曾作过精确的分析，用来检验和评价库仑理论的可靠性。当墙背垂直(α=0°)，填土水平(β=0°)，不考虑土与墙背的摩擦力(δ=0°)，由库仑理论求得的主动、被动土压力系数公式为：Ka=tan2(45°-φ/2)、Kp=tan2(45°+φ/2)，与索氏理论完全符合，说明在此种情况下，库仑理论是可靠无误的。上述两个公式亦即砂性土朗肯理论土压力系数计算公式。当α=0°,β=0°和δ≠0°时，由索氏的计算得出下列结论：库仑主动土压力误差一般不超过5%，而库仑被动土压力的误差是随着φ，特别是δ的增加而变大的，误差可超过50%，甚至更大。但索氏理论实质上还是不能完全反映复杂的实际情况，也只是一种近似方法，更何况对于复杂的填土和荷载情况，计算工作十分繁重，其实用价值不大。库仑土压力的误差主要是由于假设的滑动面为一平面而引起的。一般讲，库仑主动土压力计算实用上是足够准确的，而被动土压力与实际情况出入之大，有时不能应用于具体的工程设计中。朗肯土压力理论由于不考虑土与墙背的摩擦力，以致主动土压力偏大，而被动土压力则偏小。一般来讲，用朗肯土压力理论计算主动土压力作挡土墙的计算是比较保守的，除非墙背垂直而光滑，不能考虑墙摩擦力。当朗肯发表其土压力理论时，与库仑理论一样，仅限于无粘聚力的砂性土，后来培尔氏于1915年始将朗肯理论扩大使之适用于粘性土。(Terzaghi)太沙基认为库仑和朗肯土压力理论只适用于无挠曲的重力式挡土墙之类的挡土构筑物。

1.2 对《建筑地基基础设计规范GBJ7-89》附录11“挡土墙主动土压力系数Ka”的看法 在计算Ka的公式中，几乎所有计算主动压力的各种条件和参数如挡墙背面的角度α(注意此α与库仑公式中的α含义不一样)，墙后土坡的倾角β、墙摩擦角δ、粘性土的抗剪强度指标c、φ、地表均布荷载q以及挡墙的高度h，都已包括在内。但是粘性土的主动土压力计算毕竟是复杂的，要想用一个数学模式来全面正确地概括，这是不可能的。只有用简单的、误差又不大的计算方法，才具有真正的实际意义。笔者曾用朗肯、库仑及规范诸法计算H=8m,β=0°的直立式挡土墙(图1)的主动土压力(当粘性土的c=10kPa、φ=25°、=18.6kN/m3,q=0，δ=10°，用朗肯理论计算时δ=0°)列入表1中。从计算结果来看，如以规范法δ=10°为准，库仑理论以φD1代φ计算主动土压力与规范法算得的结果之比仅1.10；以规范法δ=0°为准，朗肯理论以φD1代φ计算主动土压力与规范法算得的结果之比为1.08。可见，用规范法算与库仑、朗肯理论算得的结果相差不大，但其算式冗繁，易得错误结果，笔者认为其实用意义不大。

表 1 主动土压力计算表

计 算 方 法 主动土压力

Ea/(kN*m-1) Ea的水平分力

Eax/(kN*m-1)

朗肯理论

(以φD代φ)

δ=0° φD1 150.4 150.4

φD2 118.7 118.7

库仑理论

(以φD代φ)

δ=10° φD1 140.5 138.4

φD2 111.9 110.2

规范法 δ=10° 127.8 125.9

δ=0° 139.6 139.6

注：表中φD1、φD2，为粘性土的第一、第二等代内摩擦角，其含义、计算方法和使用条件详见［2］。

图 1 直立式挡土墙主动土压力计算图

1.3 粘性土主动土压力计算方法的改进

在实际工程中，经常碰到粘性土。笔者认为：在计算挡墙上的主动土压力时，既要考虑粘聚力的作用，又要计及墙面摩擦力的客观存在；因此，可采用将朗肯、库仑两种理论相融合的方法来处理，即以朗肯的理论求等代内摩擦角φD，然后将φD取代φ代入库仑土压力理论的公式中以计算主动土压力。关于φD的求法详见参考文献［2］［3］。

今以一般直立式挡墙(α=0°)为例，墙后土面水平(β=0°)，先求出φD(φD1和φD2)，如挡墙高度H范围内为多层粘性土，应先求其c、φ、γ的加权平均值，然后再求φD，代入朗肯公式求得主动土压力系数Kar=tan2(45°-φD/2)，为了考虑土与墙背的摩擦作用，可将Kar乘一调整系数ξ，ξ值随φD及δ而变化，很明显，ξ以下式求得：

(1)

式中：Kac——表示按库仑公式计算的主动土压力系数，当α=0°、β=0°时：

(2)

事实上，采用ξKar求得的主动土压力实为按Kac求得的水平分力Eax，而Ea垂直分力： Eay=Eaxtanδ

(3)

式中：ξ、ξKar——可按表2查用；

δ——墙摩擦角δ，一般按(1/3～1/2)φD计。

表 2 kar、ξkar值表

φD(φD1、φD2) 20° 25° 30° 35° 40° 45° 50°

Kae(δ=0°) 0.49029 0.40586 0.33333 0.27099 0.21744 0.17157 0.13247

ξ 0.92799 0.91840 0.91134 0.90656 0.90388 0.90323 0.90456

ξKar 0.45498 0.37274 0.30378 0.24567 0.19654 0.15497 0.11983

ξ 0.89734 0.88370 0.87344 0.86620 0.86174 0.85993 0.86073

ξKar 0.43996 0.35866 0.29114 0.23473 0.18738 0.14754 0.11402

2 抗滑移稳定决定挡土墙截面的方法

关于重力式挡土墙的设计，一般先根据墙后填土性质、工程地质情况和砌筑材料等条件，凭经验初步拟定挡土墙截面的尺寸，首先应作抗滑移稳定验算，如不能满足要求，则改变截面尺寸或采取其它措施，待满足抗滑移要求后，然后再作其它各种验算。本文所提决定挡土墙截面的方法，并非先作假定，而是以抗滑移稳定为条件，经计算决定。

一般重力式挡土墙，为了增大其抗滑稳定性，并尽可能减小砌体的截面积，可将基底作成与土压力方向相反的斜坡，但其倾斜度不宜过大，以免基底和墙趾前的土体发生剪切破坏。通常，如为土质地基，可视其软硬程度，选用基底倾斜度i=0.1～0.2；岩石地基时i≤0.3。地基较软弱时，对基底的摩擦系数μ较小(见表3)，可于基底夯垫一层150mm厚，μ值较大的如砾砂或级配碎石、砂，μ值即可按新垫的材料计算。 表 3 土对挡土墙基底的摩擦系数表

土 的 类 别 摩擦系数μ

粘性土(可塑0.25＜IL＜0.75) 0.25～0.30

粘性土(硬塑0＜IL≤0.25) 0.30～0.35

粘性土(坚硬IL≤0) 0.35～0.45

粉 土(sr≤0.5) 0.30～0.40

中砂、粗砂、砾砂 0.40～0.50

碎 石 土 0.40～0.60

软质岩石 0.40～0.60

表面粗糙的硬质岩石 0.65～0.75

2.1 直立式挡土墙

如图2所示的直立式挡土墙，主动土压力的水平分力： Eax=H(H+2h0)ξKar

(4)

式中：h0——地表均布荷载当量填土高

；

ξKar——根据已知的φ、δ值查表2求得。

图 2 直立式挡土墙抗滑移截面计算图

挡墙总重：

W=0.5〔(b0+b)h1+ch2+h3)B〕γm

(5)

式中：γm——挡土墙圬工的容重，kN/m3；土压力和挡墙总重的合力R与铅直线间的交角：

(6)

而

(7)

式中：Eay——主动土压力Ea的垂直分力，用(3)式计算。当基底的倾角为ε，则R沿基底斜面的法向分力和切向分力为：

RN=Rcos(θ-ε)

(8)

Rt=Rsin(θ-ε)

(9)

因此，抗滑移安全系数为：

(10)

为了使Ks≥1.3，θ角应按下式控制：

(11)

亦即挡土墙总重应符合下式的要求：

W≥cotθ*Eax-Eay=λEax-Eay

(12)

式中：

(13)

当已知基底的坡度i=0～0.3,μ=0.25～0.50时，可求得λ值见表4。

表 4 λ值表

μ 0.25 0.30 0.35 0.40 0.45 0.50

λ i=0 5.200 4.333 3.714 3.250 2.889 2.600

i=0.10 3.355 2.953 2.635 2.377 2.164 1.984

i=0.15 2.837 2.535 2.289 2.084 1.911 1.763

i=0.20 2.451 2.214 2.016 1.848 1.704 1.579

i=0.25 2.152 1.960 1.796 1.655 1.532 1.424

i=0.30 1.914 1.754 1.615 1.494 1.387 1.292

图2中，挡土墙顶宽b0为已知(当采用浆砌块石，b0不小于0.5m，混凝土挡墙b0最小

可为0.2～0.4m)，控制台阶高宽比h3/bi≥2，h2=0.8～1.0(视基础的埋置深度而定，埋深一般不小于1.0m，墙趾覆土厚度不小于0.2m)，h1=H-h2，外墙面倾斜度为1∶n，基底的倾斜度i=1，因此b、h3、B的尺寸都可化为n的函数，故挡土墙总重W实为n的二次函数，代入

(10)式，即可求解n的最小限值。实际采用n稍大于此值，则抗滑移安全系数Ks必大于1.3。

2.2 仰斜式挡土墙

仰斜式挡土墙(见图3a)，墙背坡度愈缓，主动土压力愈小，但为了避免施工困难，仰斜墙背坡度一般不宜缓于1∶0.25，墙面坡应尽量与墙背坡平行。关于土与墙背摩擦角δ，当墙背坡不缓于1∶0.25时，可假设与墙背的仰斜角α相等，因此按库仑公式计算的主动土压力呈水平方向，这样可使计算简化。

当墙背仰斜时α值为负，故α+δ=0°，代入库仑理论的主动土压力系数公式，得：

(14)

主动土压力：Ea=KaγH(H+2Kqh0)

(15)

式中：

(16)

图 3 仰斜式挡土墙

如墙后土面呈水平状态，则β=0°，Kq=1。上述用于直立式挡土墙的计算公式(6)～(13)仍可照用，但Eax以Ea代，Eay=0，代入(12)式，可得：

W≥λEa

亦即每延米挡土墙的圬工体积：

V≥λEa/γm

先设挡墙基底的倾斜度i=0.1，墙背的倾斜度为1∶0.25，为了准确地求得挡墙的截面积，必须先求出h2。图3b为挡墙底ΔABC部分的放大图，在此三角形中：∠A=ε=tan-10.1,∠C=90°-tan-10.25，=b，先求解此三角形的a、c两边。

=0.0879912118b=D

c=(S+D)=(1.081039222+

0.879912118)b=0.98047567b

a=(S-D)=(1.081039222-

0.879912118)b=0.100563552b

h2=c*sin(tan-10.1)=0.980475b*sin(tan-10.1)

=0.097560975b

b2=c*cos(tan-10.1)=0.980475b*cos(tan-10.1)

=0.975609755b

b3=(1-0.975609755)b=0.024390245b

很明显，挡墙的截面积为：

F=Hb-0.5bh2=Hb-0.5×0.09756b2

=Hb-0.04878b2

其实V=F，故可建立以下方程式：

解此方程，即可求得b的最小限值。只要取略大于此值为挡墙的宽度，Ks就必定大于

1.3。如i=0.15、0.20，可用上述同样的方法求解c、a、h2、b2、b3诸值，并列出求解b的

71重力式挡土墙设计_重力式挡土墙

普遍方程式：

(17)

当i=0.10、0.15、0.20，b2、b3、h2、K值列入表5中，以备查用。

表 5 b2、b3、h2、K表

i b2 b3 h2 K

0.10 0.97561b 0.02439b 0.09756b 0.04878

0.15 0.96386b 0.03614b 0.14458b 0.07229

0.20 0.95238b 0.04762b 0.19048b 0.09524

3 抗倾覆稳定性验算的公式

当挡土墙截面的所有尺寸已经定出。可直接代入下列公式作抗倾覆稳定性验算。

3.1 直立式挡土墙

图1中：b=b0+nh1，

B=b1+b0+nh1,h4=iB

h3=b2-iB。

将挡土墙截面划分成①、②两个梯形，其面积及重心离前趾A点的距离各为：

F1=0.5(b0+b)h1 (18)

F2=0.5(h2+h3)B

(20)

a2=B-(B(h2+2h3))/(3(h2+h3))

(21)

总的抵抗力矩(对A点取矩)为：

Mr=mΣFa+EayB

(22)

主动土压力Ea作用点离挡墙后踵的距离：

(23)

Ea的水平分力Eax对挡墙前趾A点的倾覆力矩：

M0=Eax(z-h4)

(24)

抗倾覆安全系数：

(25)

3.2 仰斜式挡土墙

如图3a所示，将挡土墙截面划分成①、②两部分，其面积及重心离前趾A点的距离各为：

F1=bh1

(26)

a1=0.5(b1+b)

(27)

式中：b1=0.25h1=0.25(H-h2)

F2=0.5bh2

（28）

(29)

总的抵抗力矩(对A点取矩)为：

Mr=γmΣFa

(30)

挡墙顶和后踵的土压力强度各为：

e1=γh0KqKa

(31)

e2=γ(H+h0Kq)Ka

(32)

(33)

Ea对前趾A点的倾覆力矩为：

M0=Ea(z-h2)

(34)

抗倾覆安全系数：

(35)

4 墙身强度计算

4.1 法向承载力验算

重力式挡土墙墙身某截面法向承载力按无筋砌体偏心受压构件计算。按《砌体结构设计规范GBJ3-88》第4.1.5条：轴向力的偏心距e按荷载标准值计算并不宜超过0.7y,y为截面重心到轴向力所去偏心方向截面边缘的距离。当e≤0.7y时，按《GBJ3-88》第4.1.1条，承载力按下式计算：

N≤φfA

(36)

式中：φ——高厚比；

β——和轴向力的偏心距；

e——对受压构件承载力的影响系数，可根据高厚比β与矩形截面轴向力偏心方向的边长之比e/h，查《GBJ3-88》附录5附表5-1至5-5，或按附录5的公式计算。关于高厚比β，粗料石和毛石砌体应乘以系数1.5。一般验算墙身和基础结合外截面的强度。计算高厚比时，厚度可取该截面至墙顶之间的平均值。计算高度H0按上端为自由端考虑，即验算截面以上高度应乘以2。

4.2 剪切应力验算

计算截面上的剪应力应小于砌体的抗剪强度设计值。亦即：

(37)

式中：W1-1——验算截面1-1以上挡墙的自重；

Eax1-1、Eay1-1——验算截面1-1以上的主动土压力的水平分力和垂直分力；

μ——圬工与圬工间的摩擦系数，一般用0.4～0.5；

b——取挡墙的单位长度为1m；

fv——砌体的抗剪强度设计值，查《GBJ3-88》表2.2.2-1。

按上式计算的剪应力很小，有时甚至为负值，故一般可不予验算。

应力高强管桩以桩身强度高、承载力高、穿透力强、施工方便、节能环保的优异特点得到广泛的应用。但在实际施工中，经常出现静压不成功，达不到设计的贯入度和标高，进一步导致桩身断裂、承载力不住的各种质量问题。通过分析，致使管桩静压不成功的原因主要有：地质勘探资料不准确；桩身承载力确定不确切。地质勘探资料不准确 众所周知，地质情况本身很复杂，可能在一个很小的区域内会出现多种不同土质状况的起伏。有的勘探单位为节省成本，不能严格按规程布点，这样就不能给设计提供准确的地质情况。某高层住宅，设计桩长16m，设计抗压荷载标准值2400kn，地质勘探未能对地下5~8m处的中密粉砂层准确判断，导致桩在静压达到设计荷载后，却不能达到设计标高，桩普遍压入持力层5~8m，有的甚至只有3~4m，经过静载荷试验，抗压桩达到设计要求，但抗拔桩远远达不到设计要求，最后不得不通过灌注桩来处理抗拔桩。究其原因就是地质勘探不明确，粉砂持力层的起伏较大。桩身承载力确定不明确 地基勘探资料提供的地基承载力过于保守，给设计人员带来误区，通常在桩的选型上出现误差，导致桩的直径加大，桩身加长桩的密度加大，桩自身的承载力提高，这样的结果就是桩在静压的难度人为增大。在上面的工程案例中，个别部位的桩间距达到了1.2m，现场出现明显的挤土效应，并且对邻近桩身质量产生了影响。静压施工中应注意的问题 在实施施工前，必须先进行试桩，并且请勘探单位和设计单位参加，试桩数量应在整个场区范围内多点选择，至少三根，以便真实确定地质情况和桩的承载力，并且可以预防部分施工中出现的问题，还可以对设计作出调整。在上面的工程案例中，经过试桩后，设计将桩长普遍调整为11m，为建设单位节省了几十万的造价。 压桩应以压入力值和设计标高两方面来控制。压桩时应控制好终止条件：压桩的终止值可以大致通过单桩竖向承载力来判断，但因土质不同而异。桩的终止压力不等于单桩的极限承载力，应通过对比试验来确定，如终止值不能满足要求，加深或补桩以确保桩基的工程质量。 沉桩路线的选择：管桩施工时，随着桩数量的增加，各层地质构造的土体密度随之增高，土体与桩身表面的摩擦阻力也相应增加，压桩所需的压力随之增大。为使压桩中各桩的压力阻力基本接近，沉桩路线应选择单线进行，不能从两侧向中间进行（所谓关门桩）。这样地基

土在入桩挤密过程中，土体自由扩张，减少压桩的难度，避免地基土挤密造成部分桩身倾斜。 桩机配重的选择：桩机的配重应达到单桩竖向承载力极限标准值的1.2倍左右，这样就不会产生压桩接近终止值，桩机抬起时桩头和桩身的冲击，致使桩身破坏，桩身的完整性也得到保证。 控制沉桩的速度：桩身一旦进入土体，应匀速连续进行，尽量减少中途因接桩等因素造成的停息时间，这样可以减少土体重新固结造成沉桩困难。沉桩遇阻时，可以多次并逐步加载复压，这样可以消除巨厚粘土层快速沉桩卸压回弹使桩身上浮，同时也能在中密的砂土中破坏端部土体的抗剪作用，使桩达到设计标高。 在大面积管桩施工时，应控制好日压桩数量，让土体有重新排水固结的过程，避免强烈的挤土效应，这样既可以减少压桩的难度，又可以减少桩身倾斜等质量问题。 管桩的桩身长度应根据现场的地基土质

的起伏状况，选择不同的桩长，并且在压桩的过程中，先压入短桩，后压入长桩。基坑土方开挖要求 严禁边打桩便开挖，这样破坏土的平衡，造成大面积桩体失衡破坏。土方开挖的时间应该在所有桩施工完成后，让桩体过一个休止期，至少15天以上。土方的开挖路线应慎重考虑，一般应分层均匀进行，避免土体应力破坏，桩体失衡造成桩体破坏。综上所述，管桩静压施工的整个质量控制应该从地质勘探到土方开挖，应控制好各个节点，避免质量问题，达到设计效果。

关于抗倾覆稳定系数的计算，有疑问！！！

关于06年案例上午卷24题的疑惑：

墙体rG=22，墙后水平主动土和水压力合力Ea＝1550KN，做用点距墙底Za=3.6m，墙前水平向被动土和水压力合力Ep＝1237KN，做用点距墙底Zp=1.7m，问抗倾覆稳定安全系数Fs＝1.2时的墙宽度b。(示意图见2楼）

根据题意现有以下几个算法，不知到那个正确？

1．Fs=(墙重力矩－水浮力距)／（被动土压力力矩－主动土压力力矩）

2．Fs=(墙重力矩＋被动土压力力矩)／（主动土压力力矩＋水浮力距）

3．Fs=(墙重力矩＋被动土压力力矩－水浮力距)／（主动土压力力矩）

我用3种方法计算，结果如下：

方法1：6.94 方法2： 7.4 方法3：7.3

按基坑规范理解，应该采用2或3计算，其结果比较接近。

但题目给的可选答案是：

A 5.62 B 6.16 C 6.94 D 7.13

显然使用方法1计算的。

看来3种计算方法工程上都可接受，问题是我们在考试，考试时我可能会按方法2、3计算，那不就选D而错了吗？还要花不少的时间！！

大家帮忙解答一下，盼！！！

我计算的水浮力和力矩为：

墙－4米至－8米，三角形分布：Pw1=(0+10×4)b/2，力臂：2b/3，力矩：(40b^2)/3

墙－8米至－10米，矩形分布：Pw2=10×2×b，力臂：b/2，力矩：10b^2

水浮力合力力矩：(70b^2)/3

二 : 重力式挡土墙课程设计(通用版)

重力式挡土墙课程设计

重力式挡土墙课程设计

作学班学指所提

者姓名 号 级

土 木 工 程

建 筑 工 程 系

科导在交

专教院日

业 师 系 期

1

挡土墙课程设计 重力式挡土墙课程设计(通用版)

重力式挡土墙课程设计

设计任务书

一、 设计题目

本次课程设计题目：重力式挡土墙设计

二、 设计资料

1、线路资料：建设地点为某一级公路DK23+415.00~DK23+520.00段，在穿过一条深沟时，由于地形限制，无法按规定放坡修筑路堤，而采取了贴坡式（仰斜式）浆砌片石挡土墙。[www.61k.com)线路经过的此处是丘陵地区，石材比较丰富，挡土墙在设计过程中应就地选材，结合当地的地形条件，节省工程费用。

2、墙后填土为碎石土，重度?0?18kN/m3，内摩擦角??35?；墙后填土表面为水平，即??0?，其上汽车等代荷载值q?15kN/m2；地基为砾石类土，承载力特征值fk?750kPa；外摩擦角?取14?；墙底与岩土摩擦系数??0.6。

3、墙体材料采用MU80片石，M10水泥砂浆，砌体抗压强1.14N/mm2，砌体重度?0?24kN/m3。

4、挡土墙布置形式及各项计算参数如下图所示：

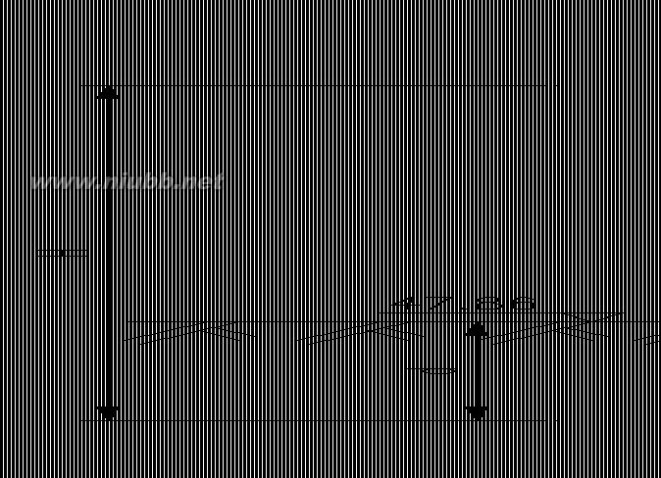
图4-1 挡土墙参数图（单位：m）

2

挡土墙课程设计 重力式挡土墙课程设计(通用版)

重力式挡土墙课程设计

目录

设计任务书·················································2

一、设计题目·············································2 二、设计资料·············································2 设计计算书·················································4

一、设计挡土墙的基础埋深、断面形状和尺寸·················4

二、主动土压力计算·······································4

1、 计算破裂角········································4 2 、计算主动土压力系数K和K1··························4

3、计算主动土压力的合力作用点·························5

三、挡土墙截面计算·······································5

1、计算墙身重G及力臂ZG·······························6

2、抗滑稳定性验算·····································6

3、抗倾覆稳定性验算···································6

4、基底应力验算·······································7

5、墙身截面应力验算···································7

四、设计挡土墙的排水措施·································8

五、设计挡土墙的伸缩缝和沉降缝···························8

六、参考文献·············································8

七、附图·················································8

3

挡土墙课程设计 重力式挡土墙课程设计(通用版)

重力式挡土墙课程设计

设计计算书

一、设计挡土墙的基础埋深、断面形状和尺寸

如图所示，挡土墙墙体高为H=8.5m，基础埋置深度d=1.5m,墙身纵向分段长度为L=10m；墙面与墙背平行，墙背仰斜，仰斜坡度1：0.2(???11.31?)，墙底倾斜度0.2:1（ω=11.31°），墙顶宽2.1m，墙底宽2m。［www.61k.com］

二、主动土压力计算

1、 计算破裂角

经试算，按破裂面交于荷载中部进行计算：

A?-H(H?2h0)tan??-tan??0.2 (H?2h0)H

????????30??11.31??15??33.69?<90°

tan?=-tan?+(cot??tan?)(tan??A) =-0.667+(0.866?0.667)(0.667?0.2)=0.486

?=26°

2 、计算主动土压力系数K和K1 K=cos(???)?tan??tan?? sin(???)

?cos（26??30?）?(tan26??tan?11.31?)?0.186 sin（26??33.69?)

4

挡土墙课程设计 重力式挡土墙课程设计(通用版)

重力式挡土墙课程设计

h0?q/γ?15/18?0.833m

h3?0

h4?H?h3?8.5-0?8.5m

K1?1?2h0h4=1?2?0.833?8.5?1.20 8.52H2

3、计算主动土压力的合力作用点

11E??H2KK1??18?8.52?0.186?1.20?145kN 22

Ex?Ecos(???)?145?cos(?11.31??15?）?144.7kN Ey?Esin(???)?145?sin(?11.31??15?)?9.3kN Zy?Hh0h4(3h4?2H)? 33H2K1

8.50.833?8.5?(3?8.5?2?8.5)??3.065m 33?8.52?1.20 =

三、挡土墙截面计算

图3-4-1 挡土墙计算图

5

挡土墙课程设计 重力式挡土墙课程设计(通用版)

重力式挡土墙课程设计

1、计算墙身重G及力臂ZG

墙身体积计算：

V1?b1(H?b1tan?0)?2.1??8.5?2.1?0.2??17m3

V2?0.5b1tan?0?0.5?2.12?0.2?0.441m3

墙身自重计算： 2

G1?V1?o?17?22?374kN

G2?V2?o?0.441?22?9.7kN

G?G1?G2?374kN?9.7kN?383.7kN

力臂ZG计算：

ZG1=0.125H+0.476b1=0.125×8.5+0.476×2.1=2.06m

ZG2=0.651b1=0.651×2.1=1.37m

ZG1G1?ZG2G22.06?374?1.37?9.7??2.04mG383.7

2、抗滑稳定性验算

（0.9G??Q1Ey）??0.9Gtan?0

?（0.9?383.7?1.4?9.3）?0.45?0.9?383.7?0.2

?230.32kN??Q1Ex?1.4?144.7?202.58kN

满足抗滑稳定性要求。(www.61k.com]

3、抗倾覆稳定性验算

墙底倾斜，需把求得的Zx、Zy修正为Zx1、Zy1。

Zy1?Zy?b1tan?0?3.065?2.1?0.2?2.645m Zx1?B?Zytan?0?2.0?3.065?0.2?1.387m

6

挡土墙课程设计 重力式挡土墙课程设计(通用版)

重力式挡土墙课程设计

0.9GZG??Q（1EyZx1?ExZy1)

?0.9?383.7?2.04?1.4?(9.3?1.387?144.7?2.645) =186.7>0

满足抗倾覆稳定性要求。（www.61k.com)

4、基底应力验算 Zn?

G1ZG1?G2ZG2?EyZx1?ExZy1G1?G2?Ey ?

e0?

max?min?374?2.06?9.7?1.37?9.3?1.387?144.7?2.645?1.053m374?9.7?9.3B2B2?ZN??1.?0.053m???0.333m 2266G?Ey?227.746e383.7?9.36?0.053?kPa??fk?750kPa 1?）?1?）???BB22?165.26

满足要求。

5、墙身截面应力验算

取墙底截面，按每延米墙长计算。

1）强度计算

Nj??kARk/?k

Nj??o?GNG?1.05?1.0?383.7?402.89kN e0.05381-256(0)81-256?()?k???0.992 e020.05321?12()1?12()2B

?kARk/??0.992?2?1?1140/2.31?979.12kN?402.89kN 满足强度要求。

2）稳定计算

Nj??k?kARk/?k

因为

7

挡土墙课程设计 重力式挡土墙课程设计(通用版)

重力式挡土墙课程设计

H/B=8.5/2=4.25<10

墙为矮墙，取?k=1，即满足稳定要求。[www.61k.com）

3）正截面直接受剪时验算

AjRj/?k?fmN1

?2?500/2.31?0.42?383.7

?594.05kN?Qj?145kN

满足受剪要求。

四、设计挡土墙的排水措施

墙身排水：设置直径为10cm的泄水孔，泄水孔向墙外倾斜5%，间距2.5m，上下交错设置。最下排泄水孔底部高墙外出地面0.3m。最下排泄水孔进水口底部铺设0.3m的黏土隔水层，并在墙顶处铺设0.3m的黏土隔水层，泄水孔进水侧设置厚度为0.3m的反滤层。在最下排泄水孔的底部设置隔水层。

五、设计挡土墙的伸缩缝和沉降缝

把沉降缝与伸缩缝结合在一起成为变形缝，沿墙长每10m布置，宽度取2cm，缝内塞沥青木板，深度为15cm。

六、参考文献

1、邓学钧 主编. 《路基路面工程》. 人民交通出版社；

2、《公路水泥混凝土路面设计规范 》（JTG D40-2010）. 人民交通出版社；

3、陈小川 周俐俐 主编. 《土力学与地基基础课程设计指南》. 中国水利水电

出版社 知识产权出版社；

七、附图

8

三 : 重力式挡土墙设计 计算过程

挡土墙设计说明书

一、设计内容

1．根据所给设计资料分析确定的挡土墙位置和类型；

2．进行挡土墙结构设计；

3.进行挡土墙稳定性分析；

4.挡土墙排水设计；

5.对挡土墙的圬工材料及施工提出要求。

二、设计步骤

1．根据所给设计资料分析挡土墙设置的必要性和可行性

此次设计的浆砌石挡土墙是为防止墙后堆积的煤矸石坍滑而修筑的，主要承受侧向土压力的墙式建筑物。

2．拟定挡土墙的结构形式及断面尺寸

给定资料：挡土墙高3.5m，堆渣坡坡比为 1:0.5 。设此挡土墙为重力式挡土墙，为增加挡土墙的稳定性，设置水平基底，为方便计算，挡土墙长度取单位长度L=1m。设墙顶宽为b1=0.5m，墙背坡比为1:0.5 ，墙面坡比为1:0.2 ，地基深h=1m，前墙趾宽为0.5m，后墙趾宽为0.5m。则可计算基底宽B=3.95m,墙身与基底交接除宽b2=2.95m。

查阅相关资料可知: 浆砌石重度γ=22kN/m3， 煤矸石堆积重度γ煤=12 kN/m3~18 kN/m3，取15 kN/m3，煤矸石内摩擦角φ=33°。地基与墙底的摩擦系数??0.4，墙背与填土间的摩擦角为

δ=0.67φ=22.11°。

挡土墙草图

3．土压力计算

计算挡土墙主动土压力Ea，首先要确定挡土墙主动土压力系数

Ka，计算公式如下：

Ka?cos(???)?2cos?cos(???)?1?

?sin(???)sin(???)??cos(???)cos(???)?22 ①

Ea=1/2*γ煤H2Ea ②

式中：

Ea——作用在挡土墙上的主动土压力（kN/m）,其作用点距基底h′（土压力图形的形心距基底的距离）。

H——挡土墙墙身高（m）；

γ煤——墙后煤矸石堆积重度（kN/m3）；

β——挡土墙墙后填土表面坡角（°）

ε——挡土墙墙背面与铅直面的夹角（°）

φ——挡土墙墙后回填煤矸石的内摩擦角（°） δ——挡土墙墙后煤矸石对墙背的摩擦角（°）

由已知条件可得：

γ煤=15 kN/m3 β=26.5651° ε=26.5651° φ =33° δ=22.11° H=3.5m 将相关数据代入①②式中，可得：

Ka=0.9914

Ea=91.08 kN/m

则土压力的水平和垂直分力分别为：

水平分力Eax=Ea cos(ε﹢δ)

=91.08×cos(26.5651°+22.11°) =60.1427 (kN/m)

垂直分力Eay=Ea sin(ε+δ)

=91.08×sin(26.5651°+22.11°) =68.4018 ( kN/m)

主动土压力的作用点距基底距离为：h′=1/3H+h=2.17m

则 ：水平分力Ex距基底左下部竖直距离为2.17m 垂直分力Ey距基底左下部水平距离为2.87m 挡土墙的自重

G=γ(b1+b2) ×H×1/2×L

=22×(0.5+2.95) ×3.95×1/2×1

=219.725 (kN/m)

重力力矩的计算：

MGⅠ=1/2×0.2H2Lγ×0.97

=1/2×0.2×3.52×1×22×0.97

=26.0517 (kN·m)

MGⅡ=b1×H×γ×1.45

=0.5×3.5×22×1.45

=55.825 (kN·m)

MGⅢ=1/2×0.5H2γ×2.28

=1/2×0.5×3.52×22×2.28

=153.840 (kN·m)

MGⅣ=Bhγ×1.975

=3.95×1×22×1.975

=171.63 (kN·m)

MG= MGⅠ+ MGⅡ+ MGⅢ+MGⅣ

=26.0517+55.825+152.840+171.63

=407.3437 (kN·m)

MEx=2.17×Ex

=2.17×60.1427

=130.5096 (kN·m)

MEy=2.87×Ey

=2.87×68.4018

=196.3132 (kN·m)

则抗倾覆力矩∑My=MG+MEy

=407.3437+196.3132

=603.6569 (kN·m)

倾覆力矩∑Mx= MEx =130.5096 (kN·m)

当|e|≤B/6时

Pmax=（Ey+G）(1+6e/B)/(BL) ③

Pmin=（Ey+G）(1-6e/B)/(BL) ④

根据资料得e=B/2-Zn

其中 Zn=(∑My-∑Mx)/(G+Eay)

=(603.6069-130.5096)/(219.725+68.4018)

=1.642

则 e=0.333＜B/6

将相关数据代入③式与④式中可求得：

Pmax =109.8424 (kPa)

Pmin=36.0478 (kPa)

Pmax /Pmin≈3 符合挡土墙基底应力最大值与最小值之比的允许值。

4、稳定性验算--抗滑稳定性和抗倾覆稳定性验算

①抗滑稳定性验算

基底抗滑力与滑动力之比称为抗滑安全系数Ks。为保证挡土墙抗滑稳定性，应验算在土压力及其他外力作用下，基底摩擦力抵抗挡土墙滑移的能力，在一般的情况下，要求抗滑安全系数Ks应满足下式： Ks=(G+Eay) μ/Eax≥1.3

代入相关数据可得 Ks=2.2＞1.3，可知挡土墙满足抗滑稳定性要求。

②抗倾覆稳定性验算

抗倾覆力矩与倾覆力矩之比称为抗倾覆安全系数Kt。为保证挡土墙抗倾覆稳定性，须验算它抵抗墙身绕墙脚趾向外转动倾覆的能力，在一般的情况下，要求抗倾覆安全系数Kt应满足下式：

Kt=∑My/∑Mx≥1.6

代入相关数据可得 Kt=4.6＞1.3，可知挡土墙满足抗倾覆稳定性要求。

5．挡土墙排水和变形缝设置

为防止地表水渗入墙背填料或地基，因此设立地面排水沟。在距地面0.3m处设置一排排水孔，排水沟的横断面为10cm×10cm的矩形，间距为2.5m。为防止因地基不均匀沉陷而引起堵身开裂，根据地基地质条件及墙高、墙身断面的变化情况，设置沉降缝。同时，为了减少圬工砌体因硬化收缩和温度变化作用而产生裂缝，须设置伸缩缝。

挡土墙排水设施如下图所示：

本文标题：重力式挡土墙设计要点-71重力式挡土墙设计
本文地址： http://www.61k.com/1072481.html