一 : 直角三角形边角关系

一、 导入

(1) 同名三角函数的大小比较

①正弦、正切是增函数．三角函数值随角的增大而增大，随角的减小而减小．

②余弦、余切是减函数．三角函数值随角的增大而减小，随角的减小而增大。

(2) 异名三角函数的大小比较

①tanA＞SinA，由定义，知tanA=a

b，sinA=a

c；因为b＜c，所以tanA＞sinA

1

努力+勤奋+信心=成功 戴氏教育集团

②cotA ＞cosA．由定义，知cosA=

○ ○bc，cotA=ba；因为 a＜c，所以cotA＞cosA． ③若0＜A＜45，则cosA＞sinA，cotA＞tanA；

○○若45＜A＜90，则cosA＜sinA，cotA＜tanA

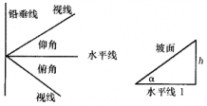
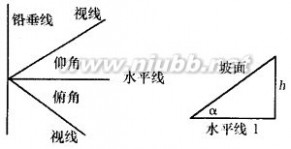
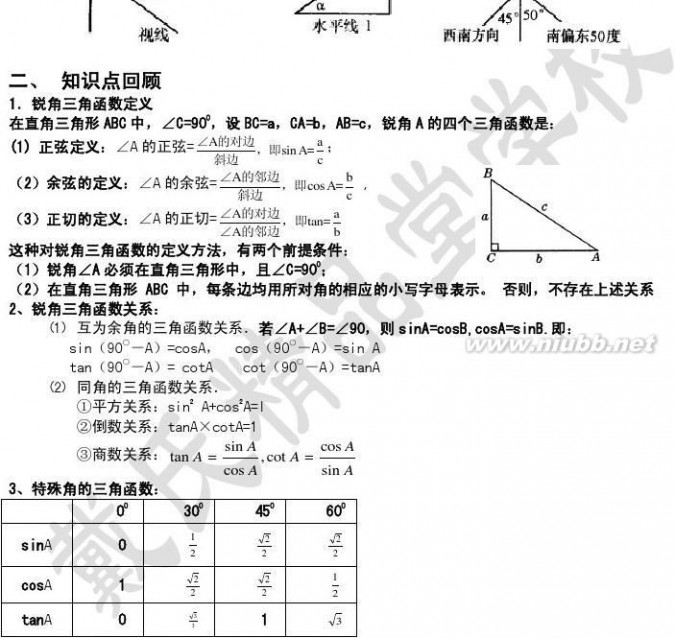
5.仰角和俯角 在视线和水平线所成的角中，视线在水平线上方的角叫仰角，在水平线下文的叫俯角（如图①）

6.7.

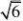
8，

(2) ?2?

? 22

2 努力+勤奋+信心=成功 戴氏教育集团

-1x3-8x3+8x3-6x2+9x0（2-2）1、设

)+(sin73°)+tan21°·tan69°，求÷的值． 2x-4x-4x+4x-x-6

??1-20sin30-2cos302、.（sin21°13′-tan21°）- （）

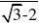
?2cos60

°,∠A=

在△

∴∠∵∴CM在△∴∠∴MD?BM?

∴CD?CM?MD?15?．

综合实践课上，小明所在小组要测量护城河的宽度。如图所示是护城河的一段，两岸

ABCD，河岸AB上有一排大树，相邻两棵大树之间的距离均为10米.小明先用测角仪在河岸CD的M处测得∠α=36°，然后沿河岸走50米到达N点，测得∠β=72°。请你根据这些数据帮小明他们算出河宽FR（结果保留两位有效数字）.

3

努力+勤奋+信心=成功 戴氏教育集团

（参考数据：sin 36°≈0.59，cos 36°≈0.81，tan36°≈0.73，sin 72°≈0.95，cos 72°≈0.31，tan72°≈3.08）

4 努力+勤奋+信心=成功 戴氏教育集团

∵69.3

千米/时<70千米/时

∴该车没有超过限速．

【点评】此题应用了直角三角形中30°角对的直角边是斜边的一半及勾股定理，也是几何与代数的综合应用

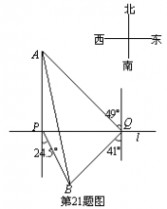
如图，自来水厂A和村庄B在小河l的两侧，现要在A，B间铺设一条输水答道.为了搞好工程预算，需测算出A，B间的距离.一小船在点P处测得A在正北方向，B位于南偏东24.5o方向，前行1200m,到达点Q

（1（2o, (2)点的G

C ? G E A

C B ? F ? F ? B E A

5 努力+勤奋+信心=成功 戴氏教育集团

【答案】解：设建筑物CD与EF的延长线交于点G，DG=x米． ????1分

在Rt△DGF中,tan??DGx，即tan??． ????2分 GFGF

DGx，即tan??． ????3分 GEGE在Rt△DGE中，tan??∴GF?xx，GE?． tan?tan?

∴

∴4∴ （）

∴x，3x＝(x＋100) ?x?1003

解得x＝50＋50＝136.6

∴CD＝CE＋ED＝(136.6＋1.5)＝138.1≈138(m)

答：该建筑物的高度约为138m．

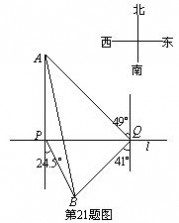
【例5】（2011四川凉山州，23，8分）在一次课题设计活动中，小明对修建一座87m长的水库大坝提

6 努力+勤奋+信心=成功 戴氏教育集团

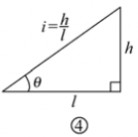
出了以下方案；大坝的横截面为等腰梯形，如图，AD∥BC，坝高10m，迎水坡面AB的坡度i?5，老3师看后，从力学的角度对此方案提出了建议，小明决定在原方案的基础上，将迎水坡面AB的坡度进行修改，修改后的迎水坡面AE的坡度i?5。 6

（1） 求原方案中此大坝迎水坡AB的长（结果保留根号）

（2） 如果方案修改前后，修建大坝所需土石方总体积不变，在方案修改后，若坝顶沿EC方向拓宽2.7m，

求坝顶将会沿AD方向加宽多少米？

?即 BE?MC?ND。 ??3x?27?4

?21?x??3x?27?4???

ND?BE?MC?6?2.7?3.3?m?。

答：坝底将会沿AD方向加宽3.3m。

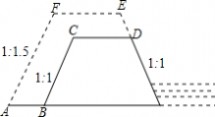
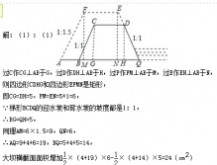
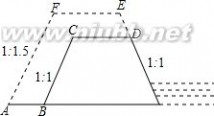
如图，某县为加固长90米，高5米，坝顶宽为4米，迎水坡和背水坡的坡度都是1：1的

横断面是梯形的防洪大坝．要将大坝加高1米，背水坡坡度改为1：1.5．已知坝顶宽不变．

7 努力+勤奋+信心=成功 戴氏教育集团

（1）求大坝横截面面积增加多少平方米？

（2

）要在规定时间内完成此项工程．如果甲队单独做将拖延10

天完成，乙队单独做将拖延6

天完成．现在甲队单独工作2天后，乙队加入一起工作，结果提前4天完成．求原来规定多少天完成和每天完成的土方数？

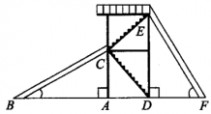
12则∠ABC+∠DFE=______．

8 努力+勤奋+信心=成功 戴氏教育集团

（2）选择

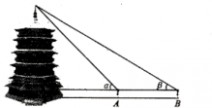
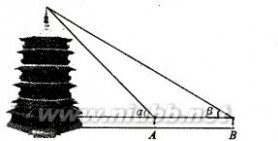
3、（2011四川绵阳10，3）周末，身高都为1.6米的小芳、小丽来到溪江公园，准备用她们所学的知识测算南塔的高度.如图，小芳站在A处测得她看塔顶的仰角α为45°，小丽站在B处测得她看塔顶的仰角β为30°.她们又测出A、B两点的距离为30米。假设她们的眼睛离头顶都为10cm，则 可计算出塔高约为(结果精确到0.01，参考数据：2=1.414，3=1.73)

4的

在Rt（35、（与

地面是 m .第16题图

【答案】1.4

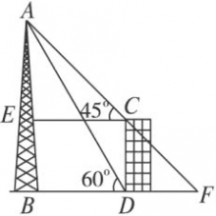
6、（2011江苏无锡，24，9分）(本题满分9分)如图，一架飞机由A向B沿水平直线方向飞行，在航线AB的正下方有两个山头C、D。飞机在A处时，测得山头C、D在飞机前方，俯角分别为60°和30°。飞机飞行了6千米到B处时，往后测得山头C的俯角为30°，而山头D恰好在飞机的正下方。求山头C、D之间的距离。

9 努力

+勤奋+信心=成功 戴氏教育集团

C

D

3

= 23．? (2分)

3

【答案】解：在Rt△ABD中，∵∠BAD = 30°，∴BD = AB·tan30° = 6 ×

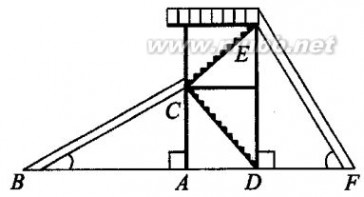
7、（角为8、如图28－2－2－10，塔AB和楼CD的水平距离为80米，从楼顶C处及楼底D处测得塔顶A的仰角分别是45°和60°.求塔高与楼高.（精确到0.01米）（参考数据2=1.414 21，=1.732 05）

图28－2－2－10

10 努力+勤奋+信心=成功 戴氏教育集团

解：在Rt△ABD中,BD=80米，∠BDA=60°，∴AB=BD·tan60°=803≈138.56（米）.

Rt△AEC中,EC=BD=80,∠ACE=45°，

∴AE=CE=80(米).∴CD=AB－AE≈58.56（米）.答:塔高与楼高分别为138.56米、58.56米.

9、某校初三课外活动小组，在测量树高的一次活动中，如图7所示，测得树底部中心A到斜坡底C的水平距离为8. 8m．在阳光下某一时刻测得1米的标杆影长为0.8m，树影落在斜坡上的部分CD= 3.2m．已知斜坡CD的坡比i=1

AB。

?1.7）

∠(

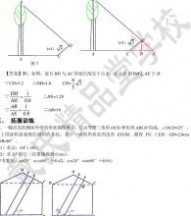
【答案】解：（1）设CD与FG交于点M，由CD∥AB，∠FGB=65°，可得∠FGC=65°，又∠OCD=25°，于是在△FGC中，可得∠CFM=90°，即GF⊥OC．

（2）过点G作GN⊥HE，则GN=EF，在Rt△GHN中，

11 努力+勤奋+信心=成功 戴氏教育集团

sin ∠EHG=GN,即GN=GH sin ∠EHG=2.6 sin 65°=2.6×0.91=2.366≈2.4cm. GH

六、反思总结

当堂过手训练 （快练5分钟，稳准建奇功）

1、如图，小明在A时测得某树的影长为2m，B时又测得该树的影长为8m，若两次日照的光线互相垂直，则树的高度为_____m.

B

23是S14、

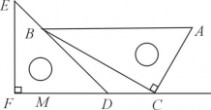
5. (点B与点F重合，EF和DF分别交AC于点M、N，DF?AB，垂足为D，AD＝1，则重叠部分的面积为 .

9 4

6、（2011四川成都，16,6分）如图，在亚丁湾一海域执行护航任务的我海军某军舰由东向西行驶．在航行到B处时，发现灯塔A在我军舰的正北方向500米处；当该军舰从B处向正西方向行驶至达C处时，发现灯塔A在我军舰的北偏东60°的方向.求该军舰行驶的路程．（计算过程和结果均不取近似值)

12

努力+勤奋+信心=成功 戴氏教育集团

北

东

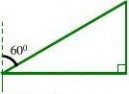
【答案】解：由题意可知，在Rt△ABC中，AB=500m，∠ACB=90°－60°=30°，

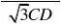
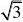
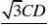
7?CD?20 35??7 5∴t?

故约7秒钟后灰太狼能抓到懒羊羊.

13 努力+勤奋+信心=成功 戴氏教育集团

二 : 直角三角形边角关系

一、 导入

(1) 同名三角函数的大小比较

①正弦、正切是增函数．三角函数值随角的增大而增大，随角的减小而减小．

②余弦、余切是减函数．三角函数值随角的增大而减小，随角的减小而增大。(www.61k.com]

(2) 异名三角函数的大小比较

①tanA＞SinA，由定义，知tanA=a

b，sinA=a

c；因为b＜c，所以tanA＞sinA

1

努力+勤奋+信心=成功 戴氏教育集团

直角三角形 直角三角形边角关系

②cotA ＞cosA．由定义，知cosA=

○ ○bc，cotA=ba；因为 a＜c，所以cotA＞cosA． ③若0＜A＜45，则cosA＞sinA，cotA＞tanA；

○○若45＜A＜90，则cosA＜sinA，cotA＜tanA

5.仰角和俯角 在视线和水平线所成的角中，视线在水平线上方的角叫仰角，在水平线下文的叫俯角（如图①）

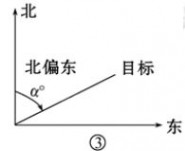
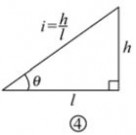
6.7.

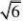
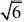
8，

(2) ?2?

? 22

2 努力+勤奋+信心=成功 戴氏教育集团

直角三角形 直角三角形边角关系

-1x3-8x3+8x3-6x2+9x0（2-2）1、设

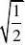
)+(sin73°)+tan21°·tan69°，求÷的值． 2x-4x-4x+4x-x-6

??1-20sin30-2cos302、.（sin21°13′-tan21°）- （）

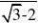
?2cos60

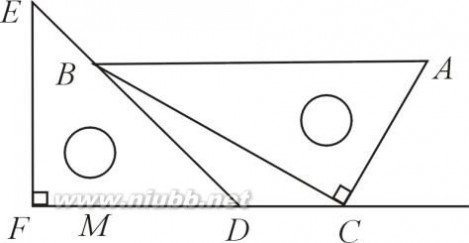
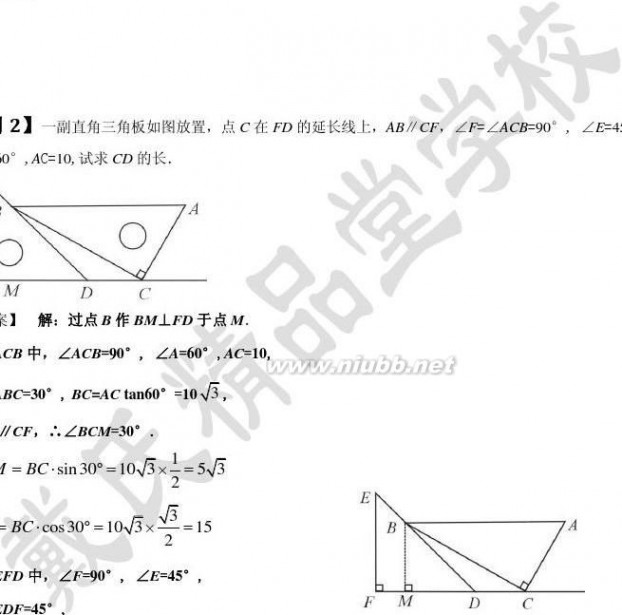
°,∠A=

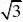
在△

∴∠∵∴CM在△∴∠∴MD?BM?

∴CD?CM?MD?15?．

综合实践课上，小明所在小组要测量护城河的宽度。[www.61k.com]如图所示是护城河的一段，两岸

ABCD，河岸AB上有一排大树，相邻两棵大树之间的距离均为10米.小明先用测角仪在河岸CD的M处测得∠α=36°，然后沿河岸走50米到达N点，测得∠β=72°。请你根据这些数据帮小明他们算出河宽FR（结果保留两位有效数字）.

3

努力+勤奋+信心=成功 戴氏教育集团

直角三角形 直角三角形边角关系

（参考数据：sin 36°≈0.59，cos 36°≈0.81，tan36°≈0.73，sin 72°≈0.95，cos 72°≈0.31，tan72°≈3.08）

4 努力+勤奋+信心=成功 戴氏教育集团

直角三角形 直角三角形边角关系

∵69.3

千米/时<70千米/时

∴该车没有超过限速．

【点评】此题应用了直角三角形中30°角对的直角边是斜边的一半及勾股定理，也是几何与代数的综合应用

如图，自来水厂A和村庄B在小河l的两侧，现要在A，B间铺设一条输水答道.为了搞好工程预算，需测算出A，B间的距离.一小船在点P处测得A在正北方向，B位于南偏东24.5o方向，前行1200m,到达点Q

（1（2o, (2)点的G

C ? G E A

C B ? F ? F ? B E A

5 努力+勤奋+信心=成功 戴氏教育集团

直角三角形 直角三角形边角关系

【答案】解：设建筑物CD与EF的延长线交于点G，DG=x米． ????1分

在Rt△DGF中,tan??DGx，即tan??． ????2分 GFGF

DGx，即tan??． ????3分 GEGE在Rt△DGE中，tan??∴GF?xx，GE?． tan?tan?

∴

∴4∴ （）

∴x，3x＝(x＋100) ?x?1003

解得x＝50＋50＝136.6

∴CD＝CE＋ED＝(136.6＋1.5)＝138.1≈138(m)

答：该建筑物的高度约为138m．

【例5】（2011四川凉山州，23，8分）在一次课题设计活动中，小明对修建一座87m长的水库大坝提

6 努力+勤奋+信心=成功 戴氏教育集团

直角三角形 直角三角形边角关系

出了以下方案；大坝的横截面为等腰梯形，如图，AD∥BC，坝高10m，迎水坡面AB的坡度i?5，老3师看后，从力学的角度对此方案提出了建议，小明决定在原方案的基础上，将迎水坡面AB的坡度进行修改，修改后的迎水坡面AE的坡度i?5。［www.61k.com） 6

（1） 求原方案中此大坝迎水坡AB的长（结果保留根号）

（2） 如果方案修改前后，修建大坝所需土石方总体积不变，在方案修改后，若坝顶沿EC方向拓宽2.7m，

求坝顶将会沿AD方向加宽多少米？

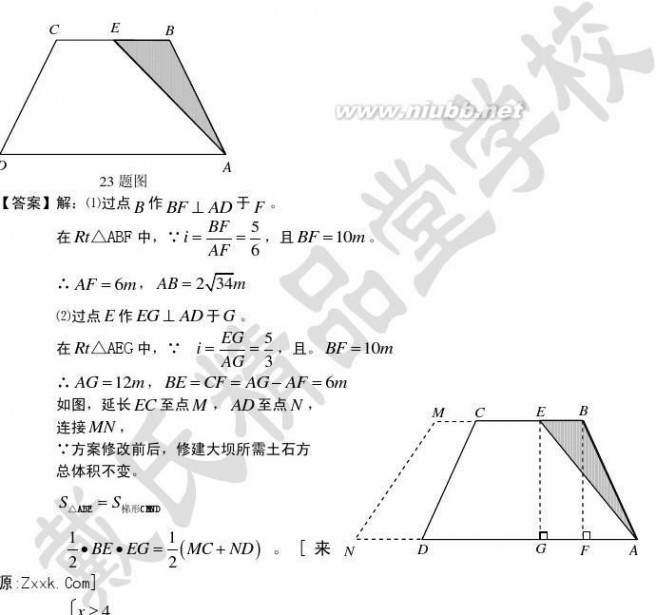
?即 BE?MC?ND。 ??3x?27?4

?21?x??3x?27?4???

ND?BE?MC?6?2.7?3.3?m?。

答：坝底将会沿AD方向加宽3.3m。

如图，某县为加固长90米，高5米，坝顶宽为4米，迎水坡和背水坡的坡度都是1：1的

横断面是梯形的防洪大坝．要将大坝加高1米，背水坡坡度改为1：1.5．已知坝顶宽不变．

7 努力+勤奋+信心=成功 戴氏教育集团

直角三角形 直角三角形边角关系

（1）求大坝横截面面积增加多少平方米？

（2

）要在规定时间内完成此项工程．如果甲队单独做将拖延10

天完成，乙队单独做将拖延6

天完成．现在甲队单独工作2天后，乙队加入一起工作，结果提前4天完成．求原来规定多少天完成和每天完成的土方数？

12则∠ABC+∠DFE=______．

8 努力+勤奋+信心=成功 戴氏教育集团

直角三角形 直角三角形边角关系

（2）选择

3、（2011四川绵阳10，3）周末，身高都为1.6米的小芳、小丽来到溪江公园，准备用她们所学的知识测算南塔的高度.如图，小芳站在A处测得她看塔顶的仰角α为45°，小丽站在B处测得她看塔顶的仰角β为30°.她们又测出A、B两点的距离为30米。[www.61k.com］假设她们的眼睛离头顶都为10cm，则 可计算出塔高约为(结果精确到0.01，参考数据：2=1.414，3=1.73)

4的

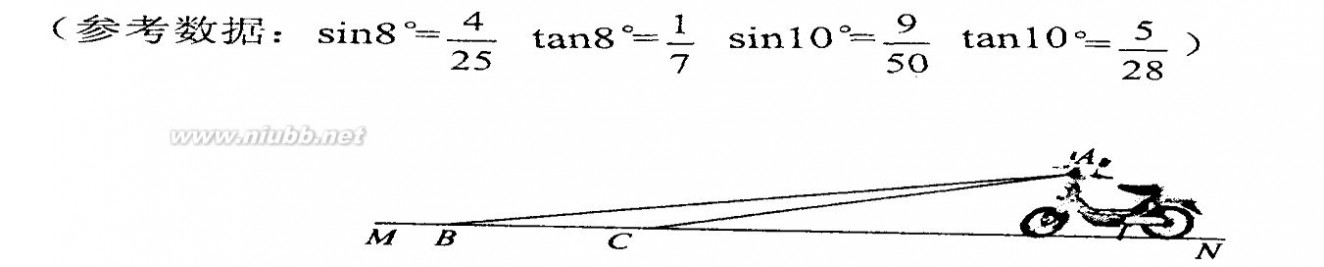
在Rt（35、（与

地面是 m .第16题图

【答案】1.4

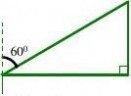
6、（2011江苏无锡，24，9分）(本题满分9分)如图，一架飞机由A向B沿水平直线方向飞行，在航线AB的正下方有两个山头C、D。飞机在A处时，测得山头C、D在飞机前方，俯角分别为60°和30°。飞机飞行了6千米到B处时，往后测得山头C的俯角为30°，而山头D恰好在飞机的正下方。求山头C、D之间的距离。

9 努力

+勤奋+信心=成功 戴氏教育集团

直角三角形 直角三角形边角关系

C

D

3

= 23．? (2分)

3

【答案】解：在Rt△ABD中，∵∠BAD = 30°，∴BD = AB·tan30° = 6 ×

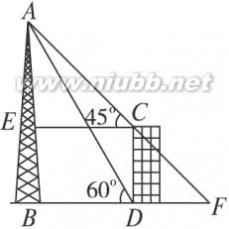
7、（角为8、如图28－2－2－10，塔AB和楼CD的水平距离为80米，从楼顶C处及楼底D处测得塔顶A的仰角分别是45°和60°.求塔高与楼高.（精确到0.01米）（参考数据2=1.414 21，=1.732 05）

图28－2－2－10

10 努力+勤奋+信心=成功 戴氏教育集团

直角三角形 直角三角形边角关系

解：在Rt△ABD中,BD=80米，∠BDA=60°，∴AB=BD·tan60°=803≈138.56（米）.

Rt△AEC中,EC=BD=80,∠ACE=45°，

∴AE=CE=80(米).∴CD=AB－AE≈58.56（米）.答:塔高与楼高分别为138.56米、58.56米.

9、某校初三课外活动小组，在测量树高的一次活动中，如图7所示，测得树底部中心A到斜坡底C的水平距离为8. 8m．在阳光下某一时刻测得1米的标杆影长为0.8m，树影落在斜坡上的部分CD= 3.2m．已知斜坡CD的坡比i=1

AB。（www.61k.com］

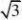
?1.7）

∠(

【答案】解：（1）设CD与FG交于点M，由CD∥AB，∠FGB=65°，可得∠FGC=65°，又∠OCD=25°，于是在△FGC中，可得∠CFM=90°，即GF⊥OC．

（2）过点G作GN⊥HE，则GN=EF，在Rt△GHN中，

11 努力+勤奋+信心=成功 戴氏教育集团

直角三角形 直角三角形边角关系

sin ∠EHG=GN,即GN=GH sin ∠EHG=2.6 sin 65°=2.6×0.91=2.366≈2.4cm. GH

六、反思总结

当堂过手训练 （快练5分钟，稳准建奇功）

1、如图，小明在A时测得某树的影长为2m，B时又测得该树的影长为8m，若两次日照的光线互相垂直，则树的高度为_____m.

B

23是S14、

5. (点B与点F重合，EF和DF分别交AC于点M、N，DF?AB，垂足为D，AD＝1，则重叠部分的面积为 .

9 4

6、（2011四川成都，16,6分）如图，在亚丁湾一海域执行护航任务的我海军某军舰由东向西行驶．在航行到B处时，发现灯塔A在我军舰的正北方向500米处；当该军舰从B处向正西方向行驶至达C处时，发现灯塔A在我军舰的北偏东60°的方向.求该军舰行驶的路程．（计算过程和结果均不取近似值)

12

努力+勤奋+信心=成功 戴氏教育集团

直角三角形 直角三角形边角关系

北

东

【答案】解：由题意可知，在Rt△ABC中，AB=500m，∠ACB=90°－60°=30°，

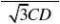
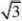
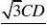
7?CD?20 35??7 5∴t?

故约7秒钟后灰太狼能抓到懒羊羊.

13 努力+勤奋+信心=成功 戴氏教育集团

三 : 什么叫垂直角度？什么叫分枝角度？它们与整形修剪有什么关系？

什么叫垂直角度？什么叫分枝角度?它们与整形修剪有什么关系？

果树枝条与垂直方向的夹角，称为垂直角度。垂直角度在30。以内的称为直立或不开张，40－60。为半开张，60－80。为开张或垂直角度大，90。左右为水平，垂直角度大于90。时称为下垂。垂直角度的大小与顶端优势有密切关系，从而影响到枝条的生长势、枝量、枝类组成．成花结果能力，以及树冠内膛的通风透光条件等。垂直角度较大时，枝条生长缓和，枝量增加比较迅速，比较容易成花、结果，树冠内的通风透光条件较好，果实品质优良，树冠内膛大枝的后部易培养结果枝组，而且在衰老更新期膛内易发生更新技。垂直角度较小时，枝条生长旺盛，枝量增加较慢，长枝比例过高，不易成花、结果，树冠内膛光照条件差，果实品质差，树冠内膛及大枝后部枝条生长弱、易枯死；衰老树回缩大枝进行更新时，仅在锯口附近萌发更新枝，下部不易萌发，因此更新比较困难。

(www.61k.com）

整形修剪中，不仅要注意干枝上的垂直角度，还需注意骨干枝之间、骨干枝与辅养枝之间在垂直角度上的差异，例如，主干疏层形要求基部主枝垂直角度较大，而上层主枝角度较小，以使膛内通风透光良好。为了保持主枝与侧枝的主从关系，要使侧枝的垂直角度大于主枝，而辅养枝的垂直角度应尽量大些，以便控制其生长势，有利于成花结果。

生产上把加大骨干枝垂直角度的方法，称为开张角度，把加大（或缩小）各种枝头垂直角度的方法，称为压低（或抬高）角度。开张角度的方法，主要是对骨干枝不过重短截、轻剪多留枝、避免选用竞争枝作为骨干枝，以及采用支撑、拉枝和背后枝换头等，还要注意多方法的综合应用。旺树的垂直角度小，重短截有促使枝条直立生长；轻剪、多留枝，可以使枝条生长缓和，其垂直角度也会较大。应用机械方法开张角度，以生长季节枝条比较柔软时进行为宜；休眠期枝脆，支、拉时易折断或劈裂。在新梢刚刚木质化时进行拿枝软化，是压低角度的好办法。枝条与其着生的母枝间的平面夹角，称为分枝角度。分枝角度过小，会形成“夹皮角”，结构不牢固、易劈裂，而且,是枝之间的空间小，影响小枝的生长。分枝角度与树种、品种的生长习性有关，柿、核桃的分枝角度较大，枣的分枝角度较小。在同一枝条上，着生节位高的枝条分枝角度较小；着生节位低的枝条分枝角度较大。为了使侧枝有较大的分枝角度，可以选用着生节位较低的枝条进行培养。

本文标题：直角三角形三边关系-直角三角形边角关系
本文地址： http://www.61k.com/1061548.html