随机过程习题解答-【程阳解答】EXCELVBARandomize生成随机数的误区

发布时间：2017-07-30 所属栏目：应用随机过程

一 : 【程阳解答】EXCELVBARandomize生成随机数的误区

【程阳解答】

EXCEL VBA Randomize 生成随机数的误区

randomize 【程阳解答】EXCELVBARandomize生成随机数的误区

更多的【程阳解答】

1个Excel_VBA随机性比对程序_06.xls

【网友问题】 来自博文留言【点击查看】

程阳老师，上面第13、14两图，也是我关心的。可是事实上很难呀，彩票的“机选”就不是随机的，而且很不随机，经常是几个号码扎堆。随便翻报纸选号，就像您说的，也不随机。我用EXCEL编了个小程序，想生成随机数Rand()，可是号码序列竟然会经常重复！真实郁闷，说白了可能最随机的数，还是把号码写在扑克牌上，洗牌抽取。可是，又太罗嗦啦。请老师指点！谢谢！

randomize 【程阳解答】EXCELVBARandomize生成随机数的误区

【程阳解答】

这位不知名的网友，你提到的博文中“第13、14两图”，我们在放在这里，大家可是进行分析，其实即使彩票从业者，大多数人对此也是毫无头绪的。你的言语告诉我，你对彩票随机性有相当的理解，否则我的解答还真是很难进行。

随机性研究，是项很重要的研究领域，这方面的成果汗牛充栋，我本人1980年代也做过随机性相关研究工作，主要是用于工业控制与检测方面。而随机性则是彩票的命门，其重要性怎么说都不过分，只不过中国彩票业研究随机性的人确实很少。这里，考虑大多数彩票同仁的理解，我尽量把你的问题，解释的通俗易懂些，冗长深奥的随机性理论我们就不谈了。

总的来说，要生成随机数，无非就是3种方法：

第一是用物理器件。这种类型的芯片现在很多，同一系列等级从军用、工业用、民用性能差异也是数量级，例如现在多数快速游戏的开奖，就是使用的这类芯片生成随机数，再通过软件转换为开奖号码。尽管这类方法可以生成所谓“真随机”数，但那是对大众理解来说的，事实上要研究解决的问题永远存在，众多学者对此的研究从无停息。

第二是软件编程与物理事件结合的方法。例如可以把鼠标的运动轨迹“当成”1种物理事件，并用相关编程，最大限度地“发挥”该物理事件的随机性。这类方法，我以为是1个不上不下的方法，在现今意义已经不大，因为如果要工业、商业应用直接用“真随机”芯片更加简单，要简单玩玩编程就能实现。

第3种就是纯软件编程实现的方法。总所周知，这种方法生成的随机数，是“随机质量”很差的“伪随机”数，但是因为简单，现实中也经常使用在要求不高的场合，例如彩票号码的“机选”即可此来简单实现，所以也会产生一些让人“揪心”的结果，并引起有关媒体的猜疑。这里要说的，许多媒体和百姓把“伪随机”当成了“作假”，其实是很片面的。其实说白了，不是彩票机构不想更加“随机”，而是理论和技术上有困难，或者要实现成本过于巨大。简单的比喻，都知道数学理论上有“圆”，但“真正的圆”现实物理世界中是没有的，地球是圆的吗？足球是圆的吗？车轮是圆的吗？彩票号球是圆的吗？严格说的都不是！甚至圆规画出来的都不是100%的“圆”，这就数学理论与现实物理世界的区别。

既然任何计算机程序语言都不可能生成真正的随机数，都是“伪随机”数，那么如何最大限度地接近真随机，就是编程者的水平问题啦。你使用的EXCEL VBA 用 Rand() 【程序中用Rnd()】函数生成随机数，出现号码序列经常重复的现象，可能的情况是——

1、忽略了Randomize 的使用。在程序开始，使用一次 Randomize 初始化是Rand() 能够随机的前提；

2、错误地多次使用Randomize 。这方面，大多数 EXCEL 的教科书甚至都是错误的，特别是在大多数使用 Rand()进行循环产生序列随机数的案例中，基本都错了。有些人认为Randomize 既然是“随机化”的，所以多多益善，在所有Rand()循环中多次调用。我只能告诉大家，这样的“后果很严重”。

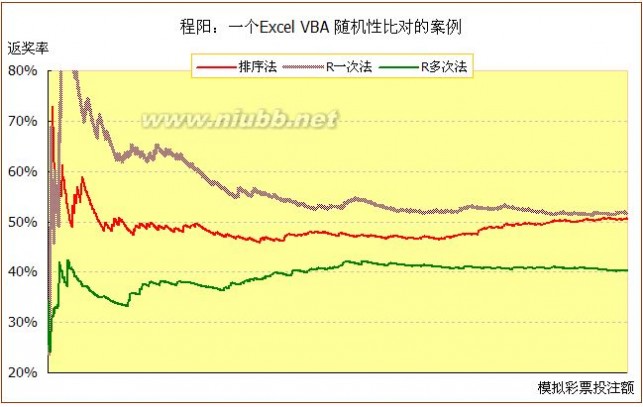
题图，给出了1个 EXCEL VBA 随机性比对的案例：“排序法”直接在页面使用Rand()，并与彩票号码两列等长排列，然后以Rand()的大小为序排序，这样可以形成一组随机彩票号码；“R一次法”“R多次法”就是上面说的使用一次、多次Randomize。我们看到，随着“模拟彩票销额”的增加，“排序法”“R一次法”的返奖率，都慢慢向50%的理论返奖率靠拢“收敛”，而“R多次法”由于严重的非随机性，导致结果“不收敛”。这是十分严重的事情，有些地方用计算机“抽号”时，发生的很多匪夷所思的现象，也许不一定是作假，而是“水平有限”所致。

randomize 【程阳解答】EXCELVBARandomize生成随机数的误区

二 : 谁养鱼？解答过程

谁养鱼？

1。在一条街上，有5座房子，喷了5种颜色。?2。每个房子里住着不同国籍的人。

3。每个人喝着不同的饮料，抽不同品牌的香烟，养不同的宠物。问题是：谁养鱼？

提示：

1、英国人住红色房子。2、瑞典人养狗。3、丹麦人喝茶。

4、绿色房子在白色房子左面。5、绿色房子主人喝咖啡。

6、抽Pall Mall香烟的人养鸟。7、黄色房子主人抽Dunhill香烟。8、住在中间房子的人喝牛奶。9、挪威人住第一间房。

10、抽Blends香烟的人住在养猫的人隔壁。11、养马的人住抽Dunhill香烟的人隔壁。12、抽Blue Master的人喝啤酒。13、德国人抽Prince香烟。14、挪威人住蓝色房子隔壁。

15、抽Blends香烟的人有一个喝水的邻居。

1使用提示：挪威人住第一间房。2使用提示：住在中间房子的人喝牛奶

3使用提示：挪威人住蓝色房子隔壁得出2号房蓝色

4使用提示：绿色房子在白色房子左面。只能是345号房又因提示 5绿色房子主人喝咖啡。所以排除3号房得出是4号房是绿色.5号房是白色，4号房的是喝咖啡

5使用提示：英国人住红色房子。第一间是挪威人住的。也就是只能3号房是英国人住的红色房子，2345的颜色都出来了。那1号房的颜色自然就是剩下的黄色了。

6使用提示：7黄色房子主人抽Dunhill香烟，11、养马的人住抽Dunhill香烟的人隔壁。得出：1号房Dunhill香烟，2号房养马

7使用提示：2、瑞典人养狗。3、丹麦人喝茶。12、抽Blue Master的人喝啤酒。喝啤酒的只能是2号或者5号房间。而瑞典人养狗也就直接排除了2号房间。也就是5号是瑞典人的养狗喝啤酒，丹麦人就只剩下2号房间了，四个国籍的都出来了，4号自然就是德国人住的了

8使用提示：德国人抽Prince香烟

9使用提示：15、抽Blends香烟的人有一个喝水的邻居。4间房的饮料出来了，剩下的是挪威人，也就是挪威人喝水，2号房抽Blends香烟

10使用提示：6、抽Pall Mall香烟的人养鸟。香烟也就只剩下3号房间的了，3号房间的人养鸟，抽Pall Mall香烟

11使用提示：抽Blends香烟的人住在养猫的人隔壁，得出1号房养猫

剩下的那位就是养鱼的了

答案：德国人养鱼

解答人：沉詸小雙

三 : 应用随机过程课后习题解答毛用才胡奇英

第一章习题解答

1．设随机变量X服从几何分布，即：P(X?k)?pqk,k?0,1,2,。（www.61k.com]求X的特征函

数，EX及DX。其中0?p?1,q?1?p是已知参数。解

fX(t)?E(e

jtx

k?0

jtk

pqk

kjtk

) ?p?(qe

k?0

jtk

=p?(qe)?

k?0

1?qejt

又

E(X)??kpq?p?kq?p2?

ppk?0k?0

D(X)?E(X2)?[E(X)]2?q （其中 ?nx

n?0?

??(n?1)x??xn）

n?0

令 S(x)??(n?1)xn

n?0

则 ?0S(t)dt?

??(n?1)tdt?

k?00

?xn?1?

n?0

1?x

?S(x)?

S(t)dt?2?(1?x)0

11x

??nxn???

(1?x)21?x(1?x)2n?0

同理 ?kx??(k?1)x?2?kx??xk

k?0

????

令S(x)??(k?1)2xk 则

k?0

?S(t)dt??(k?1)tdt??(k?1)x

k?0

k?1

??kxk）

k?1

应用随机过程应用随机过程课后习题解答毛用才胡奇英

2、（1）求参数为(p,b)的?分布的特征函数，其概率密度函数为 ?bp

p?1?bxxe,x?0?b?0,p?0 p(x)???(p)

?0,x?0?

（2）其期望和方差；

（3）证明对具有相同的参数的b的?分布，关于参数p具有可加性。(www.61k.com) 解（1）设X服从?(p,b)分布，则 ?

fX(t)??e

0jtxbpp?1?bxxedx ?(p)

?bp

p?1(jt?b)x?xedx ??(p)0

bpe?uup?1bp1?u(jt?b)x??pp?p ?(p)0(b?jt)(b?jt)(1?)b??

(?(p)??xp?1exdx) ?0

（2）?E(X)?1'pfX(0)? jb

1''p(p?1)f(0)? Xj2b2

22 E(X2)?P ?D(X)?E(X)?E(X)?2 b

（4）若Xi?(pi,b) i?1,2 则

jt?(P1?P2)fX1?X2(t)?fX1(t)fX2(t)?(1?) b

?Y?X1?X2?(P1?P2,b)

应用随机过程应用随机过程课后习题解答毛用才胡奇英

同理可得：bP?fX(t)?()i?ib?

3、设X是一随机变量，F(x)是其分布函数，且是严格单调的，求以下随机变量

的特征函数。［www.61k.com）

（1）Y?aF(X)?b,(a?0,b是常数)；

（2）Z?lnF(X),并求E(Zk)(k是常数）。

解（1）P{F(x)?y}?P{x?F?1(y)}?F[F?1(y)]?y

?y?0

? F(y)??0

?y0?y?1

??1y?1

?F(x)在区间[0，1]上服从均匀分布

fjtxejtx

?F(x)的特征函数为X(t)??edx?0?(ejt?1)

0jtjt

fY(t)?ejbtfX(at)?ejbt(ejta?1)1

jat

（2）fZ(t)?E(ejtz)?E[ejtlnF(x)]

=?ejtlny?1dy 0

=?yjtdy?1

01?jt

?f'

Z(t)?(?1)?j?(1?jt)?2

f''

Z(t)?(?1)(?2)?j2?(1?

jt)?3

3 0?y?1）（

应用随机过程应用随机过程课后习题解答毛用才胡奇英

fZ(t)?(?1)k!?j?(1?jt)?E(Zk)?(k)kk?(k?1) 1(k)kf(0)?(?1)k! Zkj

n4、设X1，X2，Xn相互独立，且有相同的几何分布，试求?Xk的分布。(www.61k.com）

k?1

解 f?Xk

k?1n(t)?E(e

n?xkk?1n) jtxkE(e) =?k?1

n =?p jt

k?11?qe

=pn(1?qejt)n =?Cnkpn(?q)kejtk

k?0?

?P{?xk?n?k}?Cnkpn(?q)k

k?1n

ejt(1?ejt)5、试证函数f(t)?为一特征函数，并求它所对应的随机变量 n(1?ejt)

的分布。

ejt(1?ejnt)1ejt(1?ejt)证（1）limf(t)?lim?lim?1 jtt?0?t?0?n(1?e)nt?0?1?ejt

ejt(1?ejnt)1(1?ejt)jt limf(t)?lim?limelim?1 jtjt??t?0?t?0?n(1?e)t?0t?0n1?e ?f(0)?1

f(t)?1? f(t)为连续函数 limt?0

应用随机过程应用随机过程课后习题解答毛用才胡奇英

??f(t

i?1k?1

?tk)?ik???

i?1k?1

ejtiejtin

{1?(jtk)}jtk

jti

n(1?jtk)

ejtiejtiejti

{1?(jtk)(1?jtk?nnjtk

=??ejtii?1k?1

n(1?jtk)

)}

i?k

1nnnj(ti?tk)l

]?i?k

=???[eni?1k?1l?1

? =???jltkik

ni?1k?1l?1e

1nnjltinn?jltk

k =??e?i??e

ni?1l?1k?1l?1

nnn

jlti

??f(t?t)?i

i?1k?1

?非负定（2）

ejt(1?ejnt)

f(t)?

n(1?ejt)

e(n?1)tj)

ejt(1?ejt)(1?ejt?e2jt?

n(1?ejt)

1njtk

=?e

nk?1

?P{xk?k}? （k?0,2,n）

6、证函数f(t)?

解（1）

为一特征函数，并求它所对应的随机变量的分布。[www.61k.com） 1?t2

??f(t?t)??

i?1k?1

应用随机过程应用随机过程课后习题解答毛用才胡奇英

=??

i?1

?ik

k?11?(ti?tk)

???

i?1

?ik

k?11?M

?0 （M?max{ti?tk）

1?i,j?n

且f(t)连续f(0)?1 ?f(t)为特征函数（2）f(t)?

11111

??[?] 1?t21?(jt)221?jt1?jt

1(jt?1)x

dx??e?(jt?1)xdx] =[?e

1jtx?x

dx =?e

2??

jtx1?x

edx

=?e2??

?P(x)?e?x

7、设X1，X2，Xn相互独立同服从正态分布N(?,?2)，试求n 维随机向量

(X1,X2,

并求出其均值向量和协方差矩阵，再求X??Xi的率密度X

n)的分布，

ni?1

函数。(www.61k.com]

解

P(x1,x2,

xn)??Pxi(xi)

i?1

1(2?)?n

exp{?

?(x?a)

ii?1

22f(t)?exp{jat??t} 又 Xi的特征函数为：Xi2

fX1,X2Xn(t1,t2

22tn)??f(ti)?exp{?(jati??ti)} 2

i?1

? 均值向量为??{?,?,?} ? 协方差矩阵为B?diag(?2,?2,?2)

又

应用随机过程应用随机过程课后习题解答毛用才胡奇英

ttf(t)?f(n,n,tnt)??f(n)?exp{jat?21n?2t2] i?1n

8、设X．Y相互独立，且（1）分别具有参数为(m,p)及(n,p)分布；（2）分别服从参数为(p1,b),(p2,b)的?分布。(www.61k.com)求X+Y的分布。

解（1）fX(t)??e

njtxkPk??e?jtxCnxpxqn?x x?0n =?(pe?it)xCnxqn?x

x?0

=qn?(

x?0np?jtx)Cnx

p?jtn =qn(1?e)

=(q?pe?jt)n

jtjtmn则 fX,Y(t1,t2)?(pe1?q)(pe2?q)

?fX?Y(t)?fX(t)fY(t)?(pejt?q)m?n

b(m?n,p) ?X?Y

（2）

jt?p1fX(t)?(1?)b

jt?(p1?p2)?fX?Y(t)?(1?) b

?X?Y?(p1?p2,b)

9、已知随机向量（X、Y）的概率密度函数为

22?4[1?xy(x?y)],?1?x,y?1 p(x,y)?? 0,其他?

求其特征函数。

解

f(t1,t2)?E{ej(t1x?t2y)} 7

应用随机过程应用随机过程课后习题解答毛用才胡奇英

j(1x?t2y)33e?(1?xy?xy)dy ＝??4

?1?11

jtx33 ＝2?e1dx?[cost2y?j(xy?xy)sint2y]dy

sint1sint2 ＝t1t2

10、已知四维随机向量(X1,X2,X3,X4)服从正态分布，均值向量为0，协方差矩阵为B?(?kl)4?4,求（X E1X2X3X4）。［www.61k.com] 解

E(X1,

?f(

t1,t4)

X4)?(j)?4[]

?(t1,t4)

' t4)?exp[?2tBt]

t1?t4?0

又

f(t1,

＝exp{?

??11

其中B??21

??31????41

1????tt}

lkl

k?1l?1

?12?22?32?42?13?23?33?43

?14??24?? ??cov(X,X) (kl,?

klkl

?34???44??

1,2 ,

E（X1X2X3X4）=?12??3

???13

11、设X1，X和相互独立，且都服从N（0，1），试求随机变量X32

Y1?X1?X2和Y2?X1?X2组成的随机向量（Y，Y）12的特征函数。

解

fX1,X2,X3(t1,t2,t3)?exp{j?tkxk}

k?1

jtkxk2e?exp{?t2?k} ＝?

k?1

＝fX1,X2,X3(u1?u2,u3,u4)

222

＝1[((u1?u2)?u1?u2)]}

12、设X1，X2和X3相互独立，都服正态分布N（0，?2），试求：

应用随机过程应用随机过程课后习题解答毛用才胡奇英

（1）随机向量的特征函数。（www.61k.com）（X1，X2，X3）

（2）设S1?X1,S2?X1?X2,S3?X1?X2?X3,，求随机向量(S1,S2,S3)的特征函数。（3） Y1?X2?X1和Y2?X3?X2组成的随机向量（Y，Y）12的特征函数。解（１）fX,X

1222

(t?t?t,t?t,t)?exp{?[(t?t?t)?(t?t)?t]?} ,X12323312323323

2,3

（２）fS,SS(t1,t2,t3)?E{exp[j(t1s1?t2s2?t3s3)]}

＝E{exp[j((t1?t2?t3)x1?(t2?t3)x2?t3x3]} ＝fX,X,X(t1?t2?t3,t2?t3,t3)

＝exp{?[(t1?t2?t3)2?(t2?t3)?t32]?2} （３）?fY1,Y2(t1,t2)?E{e

j(t1y1?t2y2)

}

＝E{exp[j(?t1x1?(t1?t2)x2?t2x3]}

2222

＝exp[?1(t?(t?t)?t]?} 112213、设，其中协方差矩阵为B=（?ld）（X，1X，2X）3服从三维正态分布N（0，B）3?3,，且

?11??22??33??2.试求。

解

222

E[(X1??2)(X2??2)(X3??2)]

＝E[X12X22X32]?E[X12X22?X12X32?X22X32]?3?4E[X12]??6

又f(t)?exp{?1 tBt}

?4f ?22

?t1t2

t1?t?2t?0

???2b 123

同理可得 E(XX)??42 1b313?2 E(X22X32)??4?2b23

22 E(X12X22X32)??6?2?2b12?2?2b13?8b12b23b13 2 ?E[(X1??

)X(?2?2

?)X?(2?3

)1b]2 b823b

14、设X1，X2，Xn相互独立同服从分布N（0，?）。试求Yn?exp(??Xi2)的期望。

i?1

应用随机过程应用随机过程课后习题解答毛用才胡奇英

解Xkn, N(0,?2) (k?1,2 令X?(x1,x2,xn) t?(t1,t2,tn) 则

1fX(t)?exp{?tdiag(?2,?2,212n2?)t}?exp{???tk} 2k?12'

n2?E(Yn)?E{exp(??tk)}

k?1

???

2?n??k?1??2?2?xk12?dk x 2xk yn?(

n2?1x)

2k12k?1n1?212?1)2)?e?ykdyk 2?????

＝k?112?1) 2?

＝(1?2?) 2?n2

15、设X．Y相互独立同分布的N(0,1)随机变量，讨论U?X2?Y2和V? 解 ?Z1?X2?Y2? ?XZ2???Y

22X的独立性。[www.61k.com) Y???x??x??z1?x?y????有

或?x??z??2y????y??y??? 则J?1?2x

y2y?xyx22??22?2??2(z2?1) y

?x2?y2

2又RX?Y(x,y)?1e2? (x,y)?R2 1?z

11e[?] ?PZ1,Z2(z1,z2)?22?(1?z2)

10 (z1?0,z2?R)

应用随机过程应用随机过程课后习题解答毛用才胡奇英

P1?zZ1)?2

1(z2e (z1?0)

P11

Z2(z2)?2??1?z2 z

22?R

?Z1服从指数分布， Z2服从柯西分布，且

对?(z2

1,z2)?R,有

PZ1,Z2(z1,z2)?PZ1(z1)?pZ2(z2)

?Z1,Z2 相互独立。［www.61k.com）

、设X． Y相互独立同服从参数为1的指数分布的随机变量，讨论U?X?Y和V?X

X?Y的独立性。

解（1）P?e?xx?0

X(x)??x?0

?e?(x?y) Px?0,y?0

X,Y(x,y)???0其它

(2) P-[u(1-v)+uv]u???ue?u0?u0?v?1

U（u,v）=eV?0其它

(3) P,v)dv???0u?0

U(u)?

???PUV(u?ue?uu?0

Pv)??v?0或v?1

V(???

?ue?udu?1

??0?v?1

? Pu,v)?P2

UV(U(u)PV(v) 对?(u,v)?R均成立

?U,V相互独立

、设二维随机变量（X，Y）的概率密度函数分别如下，试求E（XY?y)

?1?y?x

（1）y

p(x,y)???e,x?0,y?0

?y,其它

11 1617

应用随机过程应用随机过程课后习题解答毛用才胡奇英

??2e??x,0?y?x（2）p(x,y)?? ,其它?0

??证（1）E{XY?y}??xPX(xy)dx

??0??1?y?x?edxy1?y?edxy

?1??y?y?0 （2）E(XY?Y)?x?2e??xdx

2??x??edx

yy???

18、设X、Y是两个相互独立同分布的随机变量，X服从区间[0，1]上的均匀分布，Y服从参数为?的指数分布。（www.61k.com]试求（1）X与X+Y的联合概率密度；（2）D(XY?y).

解 PX(x)???1x?(0,1) ?0其它

??e??yy?0 PY(y)?? y<0?0

??e??y0?x?1y?0?PX,Y(x,y)?? 其它y<0?0

令??U?X?x?u 则J?1?0 ? ?V?X?Y?y?v?u

??e??(v?u)0?u?1v?u?PX,X?Y(u,v)?PX,Y(u,v?u)J?? 其它?011??（2）D(XY?y)?D(x)?1

3412

应用随机过程应用随机过程课后习题解答毛用才胡奇英

19、设Xn,n?0,?1,?2,???n0?是一列随机变量，且Xn???12?k1?kn?n?n???，其中K 是正常1??kn?数。（www.61k.com)试证：

（1）当k?1时，Xn几乎收敛于0。

（2）当k?2时，Xn均方收敛于0；

（3）当k?2时，Xn不均方收敛于0。证令X?0

Pkk 1?nnk k nXn ?n 0 n

Pk1?nk nk Xn2n2

Xn?0}?1 (当k?1，lim ?P{limn??n??2?0) Xn几乎肯定 kn

收敛于0

E{Xn?X}?E{Xn2}?2n2?k

limE{Xn?X}?lim2n2?k?0 当k?2时，n??n??22?Xn均方收敛于0

E{Xn?X}?0 当k?2时，limn??2

即Xn不均方收敛于0。 13

应用随机过程应用随机过程课后习题解答毛用才胡奇英

20、设XPYP??P

n???a,n???b,试证Xn?Yn?a?b. 证???0 xn?yn)?(a?b)??}=xn?a)?(yn?b)??} ?{x?

n?a?{y?

2n?b?2

?0?Pxn?yn)?(a?b)??} ?P{x??

n?a?2?P{yn?b?2?0 (n??)

? x?yP

nn???a?b

第二章习题解答

1.设X(i?1,2,)是独立的随机变量列，且有相同的两点分布???1

Y(0)?0Y,n(?)?Xi，试求：

i?1

（1）随机过程{Y(n),n?0,1,2,}的一个样本函数；

（2） P[Y(1)?k]及P[Y(n)=k]之值；

（3） P[Y(n)?k]；

（4）均值函数；

（5）协方差函数；解：（1）当Xi?1 时，(i?1,2,)，y(n)?n

（2）P{y(1)?k}?P{X??1

?k??1或1

1?k}?0其它 X1?X 2 0 -2

Pk 14 11

2 4

14 1?1?，令?

应用随机过程应用随机过程课后习题解答毛用才胡奇英

?1?1?k?2k?0

p{Y(2)?k}?P{X?1?X2?k}??1

k??2 ??0

其它

当n

Y ?n

?n?2 ?1 1 n?2 n

n?1n?10

1PC

nCnCn2k

Cn2n

Cn?1nCn

2n 2

当n

Y ?n

?n?2 ?2 ０ 2 n?2

[

1nn2

?]1

[n]k2

C2n

Cn2n

Cn2?1 Cn?1n2

2n （４）nn

E[Y(n)]?E[?xi]?1

?E(xi)

i?i?1

而E(xi)?0

?E[Y(n

?)] （５）nn

Cov[Y(n),Y(m)]?E{?xii?1

?xj]

j?1

若m?n E{?x2

k}?1

?E{x2k}?m

k?k?1

? 若n?m，则有Cov[Y(n),Y(m)]=n 即有Cov[Y(n),Y(m)]=min(n,m)

nCnn2

应用随机过程应用随机过程课后习题解答毛用才胡奇英

2.设X(t)?Acos?t?Bsin?t，其中A、B是相互独立且有相同的N(0,?2)分布的随机变量，?是常数，t?(??,??)，试求：

（1）X（t）的一个样本函数；

（2）X（t）的一维概率密度函数；

（3）均值函数和协方差函数。（www.61k.com)

解：（1）当A=B=1时，X(t)?cos?t?sin?t

（2）??20??cos?t?X(t)?(A,B)? ? (A,B)~N(0,B1) B1??2??sin?t???0??

2?X(t) ～N(0,?

) ?pX(x)??x22?2x?(??,??)

（3）E[X(t)]?0

cov[X(s),X(t)]?E{(Acos?s?Bsin?s)(Acos?t?Bsin?t)} ??2cos?(s?t)

3.设随机过程X(t)??(Ykcos?kt?Zksin?kt),t?0。其中Y1,Y2,,Yn,Z1,Z2,Zn是相互独

k?1n

立的随机变量，且Yk,Zk～N(0,?k2),k?1,2,n。

（1）求{X(t)}的均值函数和相关函数；

（2）证明{X(t)}是正态过程。

解：（1）E[X(t)]??[E(Yk)cos?kt?E(Zk)sin?kt]?0

k?1n

RX(s,t)?E[X(s)X[t]]

?E{[?(Ykcos?ks?Zksin?ks)][?(Ykcos?kt?Zksin?kt)]}

k?1k?1nn

?E[?(Yk2cos?kscos?kt?Zk2sin?kssin?kt)]

k?1

??2?cos?(s?t)k

k?1

应用随机过程应用随机过程课后习题解答毛用才胡奇英

（2）(X(t1),X(t2),,X(tn))?(Y1,Y2,,Yn,Z1,Z2,,Zn)A (Y1,Y2,,Yn,Z1,Z2,,Zn)~N(0,B)

cos?1tn???cos?ntn?222222?，B?diag(?1,?2,?k,?1,?2,?k) sin?1tn???sin?ntn???cos?1t1cos?1t2???cos?nt1cos?nt2其中A???sin?1t1sin?1t2???sin?tsin?tn1n2?由n维正态分布的线性性质得 (X(t1),X(t2),,X(tn))～N(0,A'BA) 因此X(t)是正态过程。(www.61k.com）

4.设{W(t),t?0}是参数为?2的Wiener过程，求下列过程的均值函数和相关函数：

（1）X(t)?W2(t),t?0; （2）X(t)?tW(),t?0

（3）X(t)?c?1W(c2t),t?0 （4）X(t)?W(t)?tW(t),0?t?1 解：（1）mX(t)?E[X(t)]?E[W2(t)]??2t RX(s,t)?E[W2(s)W2(t)]?E[W2(s)]?E[W2(t)]?2{E[W(s)?W(t)]}2

??4st?2?4min2(s,t) 1t

（2）mX(t)?E[tW()]?0

1111RX(s,t)?E[sW()?tW()]?stE[W()?W()] stst1t

11?st?2min(,)st

??2min(s,t)

（3）mX(t)?E[X(t)]?E[c?1W(c2t)]?c?1E[W(c2t)]?0 RX(s,t)?E[X(s)?X(s)]?E[c?1W(c2s)?c?1W(c2t)]

?c?2E[W(c2s)?W(c2t)]

?c?2??2?c2min(s,t)

??2min(s,t)

应用随机过程应用随机过程课后习题解答毛用才胡奇英

（4）mX(t)?E[X(t)]?E[W(t)?tW(t)]?0

RX(s,t)?E[X(s)X(t)]

?E{[W(s)?sW(s)][W(t)?tW(t)]}

?(1?s)(1?t)E?W(s)W(t)?

?(1?s)(1?t)?2min(s,t)

5.设到达某商店的顾客组成强度为?的Poisson流，每个顾客购买商品的概率为p,且与其他顾客是否购买商品无关，若{Y(t),t?0}是购买商品的顾客流，证明{Y(t),t?0}是强度为?p的Poisson流。[www.61k.com]

证：令Xn表示“第n个顾客购买商品”，则P(Xn?1)?p,P(Xn?0)?1?p?q且Y(t)??Xn。其中N(t)为[0,t]时间段内到达商店的顾客人数，则Y(t)的特征函数

n?1N(t)

为

fY(t)(u)?E{exp[juY(t)]} ?E{exp[ju?Xn]}

n?1N(t)

??E{exp[ju?Xk]N(t)?n}?P{N(t)?n}n?0

?k?1?N(t) n(?t)??[peju?q]ne??t

n!n?0

?ep?t(eju?1)

?{Y(t),t?0}是强度为?p的Poisson流。

6.在题5中，进一步设{Z(t),t?0}是不购买商品的顾客流，试证明{Y(t),t?0}与{Z(t),t?0}是强度分别为?p和?(1?p)的相互独立的Poisson流。证：（1）N(t)?Z(t)?Y(t)

? f

Z(t)(u)?E{exp[ju(N??Xi)]} i?1N(t)18

应用随机过程应用随机过程课后习题解答毛用才胡奇英

(?t)n

??t??E{exp[ju(n??Xi)]}?en!n?0i?1?n

1??

[?teju(peju?q)]e??t

n?0n!

?e?t(p?qeju)??t?t(1?p)(eju?1)?n

fN(u)?E{exp[juN(t)]}

??e

k?0?juk(?t)k??t?ek!

?e?t(eju?1)

?fN(u)?fY(u)?fZ(u)

?{Z(t),t?0}与{Y(t),t?0}独立且强度为?(1?p)的Poisson流。(www.61k.com）

7.设{N1(t),t?0}和{N2(t),t?0}分别是强度为?1和?2的独立Poisson流。试证明：

（1）{N1(t)?N2(t),t?0}是强度为?1??2的Poisson流；

（2）在{N1(t),t?0}的任一到达时间间隔内，{N2(t),t?0}恰有k个时间发生的概率为

pk??1

?1?

?2?1??2.(?2)k,k?0,1,2,

证：（1）fN1(t)?N2(t)(t)?E{eju(N1?N2)}

?E{ejuN1}?E{ejuN2}

?e?1(eju?1)?e

ju?2(eju?1) ?e(?1??2)(e?1)

? {N(t),t?0}是强度为?1??2的Poisson流。

（2）令T表示过程{N1(t)?N2(t),t?0}任两质点到达的时间间隔。A表示

恰有1个事件发生在{N1(t),t?0}的任一到达时间间隔内，则{N2(t),t?0}

应用随机过程应用随机过程课后习题解答毛用才胡奇英

P(A)?P{T2?T1}???2e??2xdx??1e??1ydy 0x??

8.设{N(t),t?0}是Poisson过程，?n和Tn分别是{N(t),t?0}的第n个事件的到达时间和点间间隔。（www.61k.com]试证明：

（1）E(?n)?nE(Tn),n?1,2,；

（2）D(?n)?nD(Tn),n?1,2,。证：E(Tn)?,E(?n)?,D(Tn)???1n1?,D(?n)?2n?2

?E(?n)?

nE(Tn),n?1,2, D(?n)?

nD(Tn),n?1,2,

9.设某电报局接收的电报数N(t)组成Poisson流，平均每小时接到3次电报，求：

（1）一上午（8点到12点）没有接到电报的概率；

（2）下午第一个电报的到达时间的分布。解：

10.设{N1(t),t?0}和{N2(t),t?0}分别是强度为?1和?2的独立Poisson过程，令X(t)?N1(t)?N2(t),t?0，求{X(t),t?0}的均值函数与相关函数。解：E[X(t)]?E[N1(t)?N2(t)]?E[N1(t)]?E[N2(t)]?(?1??2)t RX(s,t)?E[X(s)X(t)]?E{[N1(s)?N2(s)][N1(t)?N2(t)]}

E[N1(s)N1(t)?N1(s)N2(t)?N2(s)N1(t)?N2(s)N2(t)]

??12st??1min(s,t)?2st?1?2??22st??2min(s,t)

?(?1??2)2st?(?1??2)min(s,t)

11.设{X(t),t?0}是强度为?的Poisson过程，T是服从参数为?的指数分布的随机变量，且与{X(t)}独立，求[0,T]内事件数N的分布律。解：由[0,T]内N的分布律为： (?x)k

??xepT(x)dx P(N(T)?k)????k!?

应用随机过程应用随机过程课后习题解答毛用才胡奇英

?????k

?0xke?(???)xdx ???kk!

k!(???)k?1 k?0,1

?k??(???)k?1

第三章习题解答

1．证明Poisson随机变量序列的均方极限是Poisson随机变量。（www.61k.com］

?nk??n证：令{Xn,n?N}是Poisson随机变量序列，则对?n?N p{Xn?k}?ek?0,1 k!

E{Xn}?lim(???2)????2?E(X)，其中X为Poisson随机变量。又limn??n??22

2．设Xn,n?1,2，是独立同分布的随机变量序列，均值为?，方差为1，定义

1nYn??Xi，证明l.i.mXn??。 n??ni?1证：1n?Xk??nk?121n??[Xk?E(Xk)] nk?12

?E{?[Xk?E(Xk)]}nk?1

nn1?2E{?[Xk?E(Xk)]?[Xl?E(Xl)]}nk?1l?12

1 ?2n??cov(X

k?1l?1nnk,Xl)

?2?D(Xk)(Xn的独立性)nk?1

1??0(n??)n

?l.i.mYn??。 n??

3．研究下列随机过程的均方连续性、均方可导性和均方可积性。

（1）X(t)?At?B，其中A、B是相互独立的二阶矩随机变量，均值为a、b，方差为?12、?22；

（2）X(t)?At2?Bt?C，其中A、B、C是相互独立的二阶矩随机变量，均值为a、 21

应用随机过程应用随机过程课后习题解答毛用才胡奇英

22b、c，方差为?12、?2；、?3

（3）{N(t),t?o}是Poisson过程；

（4）{W(t),t?o}是Wiener过程。［www.61k.com)

解：（1）E[X(t)]?E[At?B]?ta?b

RX(s,t)?E{X(s)X(t)}?E{(As?B)(At?B)}

?stE(A2)?sE(AB)?tE(AB)?E(BB)

?st(??a)?sab?tab???b2

12222

是关于s, t的多项式函数

?存在任意阶的偏导数

?过程是均方连续，均方可导，均方可积。 22(2)E?X(T)??E??At?Bt?C???at?bt?c

RX(s,t)?E?X(s)X(t)?

?E?(As2?Bs?C)(At2?Bt?C)?

22?s2t2(a2??12)?s2tab?s2ac?st2ab?st(b2??2)?t2ac?tbc?c2??3

（3）由RN(s,t)??2st??min(s,t)知Poisson过程{N(t),t?o}是均方连续，均方可积的。

RN(t??s,t)?RN(t,t)?2(t??s)t??t?(?2t2??t)lim??lim??2t?s?0?s?0?s?s R(t??s,t)?RN(t,t)lim?N??2t???s?0?s

''(t,t)不存在，即均方不可导。 ?RN

（4）由RW(s,t)??2min(s,t)知Wiener过程{W(t),t?o}是均方连续，均方可积的。

RW(t??t,t)?RW(t,t)0?lim?0?t?0?t?t?0?t RW(t??t,t)?RW(t,t)lim???2?t?0?tlim?

''(t,t)不存在，即均方不可导。 ?RW

应用随机过程应用随机过程课后习题解答毛用才胡奇英

4．试研究上题中过程的均方可导性，当均方可导时，试求均方导数过程的均值函数和相关函数。（www.61k.com]

解：（1）均方可导

mX'(t)?a

''RX'(s,t)?Rst(s,t)??12?a2

2又RX(s,t)?st(?12?a2)?ab(s?t)??2?b2

1{RX(s??s,t??t)?RX(s??s,t)?RX(s,t??t)?RX(s,t)}?t?0?t?s?s?0lim

?lim12{(s??s)(t??t)(?12?a2)?ab(s??s)(t??t)??2?b2?t?0?t?s?s?0

2?[(s??s)t(?12?a2)?ab(s??s?t)??2?b2]

2?[s(t??t)(?12?a2)?ab(s?t??t)??2?b2]

2?[st(?12?a2)?ab(s?t)??2?b2]}

?lim1{(?12?a2)?s?t}??12?a2???t?0?t?s?s?0

?XT均方可微。

（2）均方可导，且

E[X'(t)]?mX'(t)?2at?b

RX'(s,t)?R(s,t)?[(a??)s?2t?abs?abs?2t?(b??)s?ac?2?bc?0]''ts2122222's

2?4(a2??12)st?2abs?2abt?b2??2?0 ?4(a??)st?2ab(s?t)?b??22

1222

（3）Poisson过程{N(t),t?o}均方不可导。

（4）Wiener过程{W(t),t?o}均方不可导。

5．求下列随机过程的均值函数和相关函数，从而判断其均方连续性和均方可微性。

（1）X(t)?cos(?t??)，其中?是常数，?服从[0,2?]上的均匀分布；

（2）X(t)?tW(),t?0，其中W(t)参数为1的Wiener过程；

23 1t

应用随机过程应用随机过程课后习题解答毛用才胡奇英

（3）X(t)?W2(t),t?0，其中W(t)参数为?2的Wiener过程。［www.61k.com］解：（1）E{X(t)}?1

2??2?

0cos(?t??)d??2?1sin(?t??)?0。 02?

RX(s,t)?E{X(s)X(t)}?E{cos(?s??)cos(?t??)}

12??[cos((t?s)?2?)?cos((t?s)?)]d?4??0 1?cos?(t?s)2

（2）E{X(t)}?E{tW()}?0

当s?t，RX(s,t)?E{tsW()W()}?stE{[W()?W()?W()]W()} ?stE{W2()}?st?min(,)?s ?RX(s,t)?min(s,t)?min(s,t)

?均方连续，但均方不可微，均方可积。 1t11st1s1t1s1t1t1t1t

（3）E{X(t)}?E{W2(t)}??2t

??4s(t?2s)s?tRX(s,t)?E{W(s)W(t)}??4 s?t??t(s?2t)s22

?均方连续，但均方不可微，均方可积。

6．均值函数为mX(t)?5sint、相关函数为RX(s,t)?3e?0.5(t?s)2的随机过程X(t)输入

X(t)微分电路，该电路输出随机过程Y(t)?X'(t)，试求Y(t)的均值函数和相关函数、

和Y(t)的互相关函数。

解：E[Y(t)]?E[X'(t)]?mX(t)?(5sint)t'?5cost '

RY(s,t)?E[Y(s)Y(t)]?E[X'(s)X'(t)]

?0.5(t?s)2'2?0.5(t?s)2?RX(s,t)?(3e?(t?s))t?3[1?(t?s)]?e ?s?t

RXY(s,t)?E[X(s)Y(t)]?E[X(s)X'(t)]??3(t?s)e?0.5(t?s) 2

7．试求第3题中可积过程的如下积分： 24

应用随机过程应用随机过程课后习题解答毛用才胡奇英

1t1t?LY(t)??X(u)du Z(t)??X(u)du t0Lt

的均值函数和相关函数。（www.61k.com）

t11t1Au2解：（1）Y(t)??0(Au?B)du?(?Bu)?At?B 02tt2

?E[Y(t)]?at?b 2

111ABABRY(s,t)?E{(As?B)(At?B)}?E{A2st?s?t?B2} 22422st1 ?(?12?a2)?(?22?b2)?ab(s?t) 42

t?L1t?L1Au2又Z(t)??t(Au?B)?(?Bu)?At?AL?B tLL2

?E[Z(t)]?a(t?L)?b

RZ(s,t)?E{[A(s?L)?B][A(t?L)?B]}

2 ?(s?L)(t?L)(?12?a2)?(?2?b2)?ab(s?L)?ab(t?L)

tAt2Bt1t1Au3Bu2

2（2）Y(t)??0(Au?Bu?C)du?(??Cu)???C 0tt3232

at2bt??c ?E[Y(t)]?32

As2BtAt2BtRY(s,t)?E{(??C)(??C)} 3232

1st21B?(t?s)BC?C2} 342tsabtsacst2bc2(t?s)?(t2?s2)?(?2?b2)?(t?s)??3?c2 ?()2(?12?a2)?36342 ?E{()2A2?(t2s?ts2)AB?(t2?s2)AC?ts316Z(t)?t?L1t?L1A3B22 (Au?Bu?C)du?(u?u?Cu)?ttLL32

2L2L?A(t?tL?)?B(t?)?C 32

L2LE[Z(t)]?a(t?tL?)?b(t?)?c 322

应用随机过程应用随机过程课后习题解答毛用才胡奇英

L2LL2L2RZ(s,t)?E{[A(s?sL?)?B(s?)?C][A(t?tL?)?B(t?)?C]} 32322

2L2LL2?(??a)(s?sL?)(t?tL?)?(?2?b2)(s?)(t?)3322

L2L2L2L2

2222 ?(?3?c)ab[(s?sL?)?(t?tL?)?(s?)(t?tL?)] 3323

L2L2LL22?ac[(s?sL?)?(t?tL?)?bc[(s?)?(t?)]]33222122

(3)Y(t)?1t1t?LN(u)duZ(t)?N(u)du ??0ttL

t11t?u2t?tE[Y(t)]?E[?N(u)du]???udu?? 0tt02t02

)当s?t时 RY(s,t?1E[Y(s)Y?(]ts?t

0E{N(u)N( v)dud}v

1st1st???RN(u,v)dudv???[?uv?min(u,v)]dudvts00ts00 2?st?s??(3t?s)46t

??2st?s?(3t?s)?s?t?46t ?RY(s,t)??2s?t??st??t(3s?t)?6s?4

t?L11t?L?E[Z(t)]?E[?N(u)du]???udu?(2t?L) tLLt2

当o?t?s?L

)EZ[s(Zt)?(2E RZ(s,t?1

L?s?L

s)( )?{NuNv(dudvt?tL}

1?2L??ss?Lt?Lt[?uv?min(u,v)dudv]

LL(s?t)11?(s?)(t?)???2[3(s?L)2?2(s?L)3?t3]22L26L

当?L?t?s?0时

L(s?)t11???2?[t32(?L2L2L6

1t1t?L(4)Y(t)??0W(u)du Z(t)??tW(u)du tL

1t E[Y(t)]??0E[W(u)]du?0 E[Z(t)]?0 t)(?s RZ(s,t?)? 26 L23)?t2?(L3 )s]

应用随机过程应用随机过程课后习题解答毛用才胡奇英

,t)?1st

ts?s

0?t0Ru,v)dudv??2RY(sW(ts?0?0min(u,v)dudv

????sduu0vdv??s0udu?t0?udv

?tvts

??0dv?0udu??0vdv?vdu

??2

??s

??6t(3t?s)s?t

??2t

??6s(3s?t)s?t

R(s,t)?1s?Lt?L?2Lt?LZL2?s?tRW(u,v)dudv?L2?s?s?tmin(u,v)dudv

??2s?Lus?Lt?Lvdv??s?Lu?L2[?tdu?tvdv??sudu?ttdu?tvdv](0?t?s?L)???2

?(0?s?t?L ???L2)

??2s?L

?2?sudu??2(s?L)(s?L?t)

?L2??2s?L

??L2?sdu?t?Ltvdv??2(t?L2)(t?s??L)

8．设随机过程X(t)?Ve3tcos2t，其中V是均值为5、方差为1的随机变量，试求随机过程Y(t)??t

0X(s)ds的均值函数、相关函数、协方差函数与方差函数。[www.61k.com］

解:E[Y(t)]??t3s5e3t

05ecos2sds?13(2sin2t?3cos2t?3) RY(s,t)??s?v)

0?t0E(v2)e(ucos2u?cos2vdudv

?26?s

0e3ucos2udu?t0e3vcos2vdv

?26[e3s

13(2sin2s?3cos2s?3)?e3t

13(2sin2t?3cos2t?3)]

2e3(s?t)

?13(2sin2s?3cos2s?3)(2sin2t?3cos2t?3)COVY(s,t)?RY(s,t)?mY(s)?mY(t) ?2e3(s?t)

13(2sin2s?3cos2s?3)(2sin2t?3cos2t?3)

应用随机过程应用随机过程课后习题解答毛用才胡奇英

D[Y(t)]?RY(t,t)?[mY(t)]2

26t25e(2sin2t?3cos2t?3)2?2e6t(2sin2t?3cos2t?3)213 13 6te?(2sin2t?3cos2t?3)2

169?

9．设{W(t),t?0}是参数为?2的Wiener过程，求下列随机过程的均值函数和相关函数。[www.61k.com］

（1）X(t)??t

0W(s)ds,t?0；

（2）X(t)??t

0sW(s)ds,t?0；

（3）X(t)??t?1

t[W(s)?W(t)]ds,t?0

解：（1）E[X(t)]??t

0E[W(s)]ds?0

RX(s,t)??s

0?t0min(u,v)dudv

????2[

??sust?2s20du?0vdv??0udu?udv]?6(3t?s)

s?t

??2t2 s?t

??6(3s?t)

（2）E[X(t)]?0

X(s,t)??s

0?0uvmin(u,v)dudv 5

?2?su2s2t2st2s3s5?2s3

??0udu?0vdv??0udu?uvdv??(15?6?10)?30(5t?s)

?2t3

30(5s2?t2)

（3）E[X(t)]?0

R?1

X(s,t)??s

s?t?1tE{[W(u)?W(s)][W(v)?W(t)]}dudv

??01?s?t或s?t?1 ????t?1s?12

t?s?min(u?s,v?t)dudvs?t?s?1? ?s?1t?1

??s?t?2min(u?s,v?t)dudvt?s?t?1

28 s?ts?t

应用随机过程应用随机过程课后习题解答毛用才胡奇英

??0?3223?2(s?1)t(s?1)t(s?1)t ???[???]6226??2(t?1)3s(t?1)2s2(t?1)s3

???]??[6226?1?s?t或s?t?1s?t?s?1 t?s?t?1

?X'(t)?aX(t)?010．求一阶线性随机微分方程?(a?0)的解及解的均值函数、相关X(0)?X0?

函数及解的一维概率密度函数，其中X0是均值为0、方差为?2的正态随机变量。[www.61k.com]

解：（1）dx?x???adt

?c ?lnx??at?lnc ?X(t)?ce?at ?X(0)

?X(t)?X0e?at 解过程为：{X0e?at,t?0}

（2）E[X(t)]?E[X0e?at]?0

RX(s,t)?E{X0e?a(s?t)}??2e?a(s?t)

FX(x)?P{X?x}?P{X0e?at?x}?P{X0?

xe?at}?FX0(xe?at)

PX(x)?F(x)?eF(xe'

Xat'X0?at?)?eatx2e2at2?2

11．求一阶线性随机微分方程的解及解的均值函数、相关函数。

?Y'(t)?X(t),t?[a,b]（1）?(a?0)，其中X(t)是一已知的二阶均方连续过程，Y0是与Y(a)?Y0?

X(t)独立的均值为m、方差为?2的随机变量。

?Y'(t)?aY(t)?X(t),t?0（2）?(a?0)，其中X(t)是一已知的均值函数为mX(t)?sint、Y(0)?0?

相关函数为RX(s,t)?e??t?s(??0)的二阶均方连续过程。解：（1）?YY(t)dt??aX(u)du '0Yt

Y(t)?Y0??aX(u)du

?Y(t)?Y0??aX(u)du

29 tt

应用随机过程应用随机过程课后习题解答毛用才胡奇英

即方程的解为：Y(t)?{Y0??aX(u)du,t?[a,b]}

E[Y(t)]?E[Y0??aX(u)du]?E[Y0]?E[?aX(u)du]?m??amX(u)du

（2）均方解为：Y(t)??0X(s)e?a(t?s)ds ?E[Y(t)]??0mX(s)e?a(t?s)ds??0sins?e?a(t?s)ds?

RY(s,t)??s

0ttttttt1(e?at?cost?asint) 21?a?t0e???v?e?a(s?t?u?v)dudv

（当t?s时）

??dv?e00tv??(v?u)?e?a(s?t?u?v)

vdu??dv?e??(v?u)?e?a(s?t?u?v)du0vts?e?a(s?t)?t

0e(a??)vdv?e0(a??)udu?e?a(s?t)?t0e(a??)vdv?e(a??)uduvs

e?a(s?t)t(a??)v(a??)ve?a(s?t)t(a??)v(a??)s(a??)v?e[e?1]dv?e[e?e]dv a???0a???0

e?a(s?t)12at1e?a(s?t)e(a??)s

(a??)t1(a??)t?[(e?1)?(e?1)]?[(e?1)?(e2at?1)]a??2aa??a??a??2a

1??(s?t)??a(s?t)?(?t?as)?(at??s)??(s?t)?2[e?e?(1?)e?e?e]2a??aa

第四章习题解答

1.随机过程X(t)?Acos(wt??)，其中A具有Rayleigh分布，即其概率密度函数为

?xx2

??2exp(?2?2),x?0??P(x)??(??0)

?0,x?0???

式中?服从区间[0,2?]上的均匀分布，且A、?相互独立，试研究X是否为平稳过程。（www.61k.com）

解: E[X(t)]?E(A)E[cos(?t??)] ??2?x2x21 ??2exp(?2)dx??2?2?0?cos[?t??]d? 0

RX(s,t)?E{Acos(?s??)?cos(?t??)}

应用随机过程应用随机过程课后习题解答毛用才胡奇英

2 ?E(A)E[cos(?s??)?cos(?t??)]

x3x21??2exp(?2)dx?{cos[2???(t?s)]?cos(t?s)}d???2?4?00??2?

?2?2?2?cos?(t?s) 4?

2??cos?(t?s)

?{X(t),t?T}是平稳过程.

2、X是一平稳过程，且满足，称X为周期平稳过程，T为其周期，试求X的相关函数也是以T为周期的周期函数。(www.61k.com）

解：是平稳过程，

?E(X)?m,RX(s,t)?R(?),(??t?s,s?t)

又RX(??T)?E{X(s)X(t?T)}?E{X(s)X(t)}?RX(?)

?RX(?)以T为周期.

3、设 X、Y是两个相互独立的实平稳过程，试证明Z(t)?X(t)?Y(t)也是平稳过程。解 E[Z(t)]?E[X(t)?Y(t)]?E[X(t)]?E[Y(t)]?mX?mY

RZ(s,t)?E{Z(s)Z(t)}

?E{[X(s)?Y(s)]?[X(t)?Y(t)]}

?E{X(s)X(t)?X(s)Y(t)?Y(s)X(t)?Y(s)Y(t)}

?RX(?)?2mXmY?RY(?)

?Z(t)也是平稳过程

4、设是n阶均方可微的平稳过程，证明{X(n)(t),???t???}是平稳过程，且

(2n)RX(n)(?)?(?1)nRX(?)

解： E{X(n)(t)}?(mX)t(n)?0

应用随机过程应用随机过程课后习题解答毛用才胡奇英

?2?'''R(s,t)?RX(s,t)?[?RX(?)]??RX(?) ?s?t?t''

利用归纳法可得

(n)(2n)RX(?)?(?1)(n)RX(?)

?{X(n)(t),t?R}平稳过程

5、设{X(n)}是一均值为0的平稳时间序列，证明：

（1）Z(n)?AX(n)?BX(n?m)扔是一平稳时间序列；

（2）若数列{Ak}绝对收敛，即?Ak???，则Z(n)?

k????k???(?AXnk?k?)扔是一平稳时间

序列；

（3）若{X(n)}是一白噪声，试求Z(n)?

k????AX(n?k)的相关函数及其谱函数。（www.61k.com］ k?

解（1）E[Z(n)]?E{AX(n)?BX(n?m)}

=AE{X(n)}?BE{X(n?m)}

RZ(s,t)?E{Z(s)Z(t)}

?E{[AX(s)?Bx(s?m)][AX(t)?BX(t?m)]}

?E{AX(s)X(t)?ABX(s)X(t?m)?BAX(s?m)X(t)?BX(s?m)X(t?m)}?ARX(t?s)?ABRX(t?m?s)?BARX(t?m?s)?BRX(t?s) 2222

? Z(n)是一平稳时间序列

(2) E[Z(n)]?E{?AkX(n?k)}?

k?????k????AE[X(n?k)]?0 k??

RZ(s,t)?E{?Ak1X(s?k1)?

k1?????k2??????Ak2X(t?k2)}

应用随机过程应用随机过程课后习题解答毛用才胡奇英

k1???k2?????????Ak1Ak2RX(t?s?k2?k1)

Ak1(又RZ(s,t)?

k1??????k2??????Ak2??)

? Z(n)仍是一平稳时间序列

（3）RZ(s,t)?RZ(?)? ?

SZ(?)?

?k1???k2?????????????Ak1Ak2RX(??k2?k1) k1???k2?????Ak1Ak2N0?(??k2?k1) ????e?j???Rz(?)d?

? ??e

???j??k1???k2???

?????Ak1Ak2N0?(??k2?k1)d?

?k1???k2?????????Ak1Ak2N0?e?j???(??k2?k1)d? ??

k1???k2?????

其中 Ak1Ak2N0ej?(k1?k2) （注：白噪声过程X的谱密度为SX(?)?N0(常数)，??R，相关函数RX(?)?N0?(?)，

?(x)??

6、设X(t)是雷达在a?0,x?0 ） ??,x?0t时的发射信号，遇目标返回接收的微弱信号是aX(n??)，1，?1是信号返回时间，由于接收到的信号总是伴有噪声的，记噪声为N(t)，于是接收机收到的全信号为：Y(t)??X(t??1)?N(t)，若X、Y是平稳相关的平稳过程，试求；进而，若N(t)的均值为0，且与X(t)相互独立，试求RXY(?)。（www.61k.com)

解：（1）RXY(?)?E{X(s)Y(s??)}

?E{X(s)[?X(s????1)?N(s??)]}

应用随机过程应用随机过程课后习题解答毛用才胡奇英

?E{?X(s)?X(s????1)?X(s)N(s??)} ??RX(???1)?E{X(s)N(s??)]

（2）RXY(?)??RX(???1) 7设E{X(t)X(t??)}和E{X(t)X(t+?)}，其中?是服从区间[0,2?]上均匀分布的随机变'''量，试证：

（1）{Xn,n?0,?1,?2,}是一平稳时间序列；

（2）{X(t),???t???}不是平稳过程。［www.61k.com）

1解：（1）E(Xn)?E(sin?n)?2?2??sin(?n)d??

0?1cos?n2?n2?0?0

RX(n,m)?E{Xn,Xm}?E{sin?n?sin?m} 1?2?

1 ?4?2??sin?n?sin?md? 02??[cos(m?n)??cos(n?m)?]d? 0

0 ?sin(m?n)?sin(m?n)??4?(m?n)2?(m?n)

n?0 ?{X}是一平稳时间序列

1（2）E[X(t)]?2?

1 RX(s,t)?2?2??sint?d??02??1cot?2?t2?0?1(1?cos2?t) 2?t?sins??sint?d? 0

1 ?4?2??[cos(t?s)??cos(t?s)?]d? 0

0 ?

?11[sin(t?s)?4?t?s?1sin(t?s)?t?s2?0] 111[sin2?(t?s)?sin2?(t?s)] 4?t?st?s

? {X(t),t?R}不是平稳过程 34

应用随机过程应用随机过程课后习题解答毛用才胡奇英

8、设{X(t),为零均值的正交增量过程，EX(t?X(s)?t?s，试证???t???}

Y(t)?X(t)?X(t?1)是一平稳过程。（www.61k.com） 2

解：E{Y(t)}?E{X(t)?X(t?1)}?E{X(t)}?E{X(t?1)}?0

RY(s,t)?E{Y(t)Y(s)}

?E{[X(s)?X(s?1)][X(t)?X(t?1)]}

?E{X(s)X(t)}?E{X(s)X(t?1)}?E{X(s?1)X(t)}?E{X(s?1)X(t?1)}

? 11E{X2(s)?X2(t)?[X(s)?X(t)]2}?E{X2(s)?X2(t?1)?[X(s)?X(t?1)]2} 22

11?E{X2(s?1)?X2(t)?[X(s?1)?X(t)]2}?E{X2(s?1)?X2(t?1)?[X(s?1)?X(t?1)]2}22

22221?{EX(s)?X(t?1)?EX(s)?X(t)?EX(s?1)?X(t)?EX(s?1)?X(t?1)} 2

1?{s?t?1?2s?t?s?t? 2

? Y(t)是一平稳过程。

9、设{X(t),t?0}是一平稳过程，均值mX?0，相关函数为RX(?)，若

（1）RX(?)?e?a,a?0

?1?,?1

（2）RX(?)?? ??0,其它?

1令Y(t)??X(s)ds，T是固定的正数，分别计算{Y(t),t?0}的相关函数。 T0

1解：（1）RY(s,t)?E{Y(s)Y(t)}?E{2Tstt?X(u)du??X(v)dv} 00

1 ?2T

sST??e00??u?vdudv st11??(u?v)dv?2?du?e??(v?u)dv 当s?t时，RY(s,t)?2?du?eT00T0uu

应用随机过程应用随机过程课后习题解答毛用才胡奇英

1s1s?au?a(t?u)(1?e)du?(1?e)du2?02?0aTaT11?aus11a(u?t)s?[(u?e)]?[(u?e)]2200aTaaTa?

11?as1?a(s?t)11?at[2s?ee??e]2aTaaaa

1?22[2as?e?as?e?at?e?a(s?t)?1]aT?

1? RY(s,t)?a2T2[2amin(s,t)?e?as?e?at?e?at?s?1]

（2）RY(s,t)?1

T2??(1?u?v)dudv 00st

当0?t?1?s时

RY(s,t)?v1t1t1t1sdv(1?v?u)du?dv(1?u?v)du?dudv 2?02?02?1???0v0TTT

1tv21tu2112?2?(v?v?)dv?2?[(1?v)u?]du?2(s?1)tT02T020T?11213t1(v?v)?02T2T226?t

0(2v?v2?1)dv?1(s?1)t2T

t2t1?2(3?t)?2(?t2?t?1)?2(s?1)t6T6TT

当0?s?1?t时

ust1sRY(s,t)?2{?du?(1?u?v)dv??du?(1?v?u)dv} 000uT

s1su2t2u2

?2{?(u?)du??[u(t?1)?t??]du}0T0222

1s2s3ssts3

?2{(?)?(t?1)?(1?t)? T23226

s?2[s(1?s)?(1?t)2]2T

当0?t?1?s时

RY(s,t)?t1222[t(1?t)?(1?s)]?[t(1?t)?t(1?s)] 222T2T

当1?s?t时

1sust1t11RY(s,t)?2{?du?dv??du?(1?u?v)dv??du?(1?v?u)dv??du?(1?v?u)dv}00101u01T

应用随机过程应用随机过程课后习题解答毛用才胡奇英

ss11t2u2t21

?2{1??2udu??[t??u(t?1)?]du??[(??t?)?u(t?1)]du}

110T22221s2111t2s3?1112

?2{1???(t?1)(s?1)?(s?1)?(s?1)??(t?1)2?(t?s)} T2222262211111

?2{(s2?1)(1?t)?(s3?1)?(s?t)?(t?1)2}T2622

当1?t?s时

RY(s,t)?

1223

[3(s?1)(1?t)?3(s?t)?3s(t?1)?(s?1)] 26T

10、设平稳过程{X(t),t?0}的相关函数为RX(?)?数。(www.61k.com）

(1)判断X是否均方可导，说明理由；

(2)计算E{X(t)X'(t??)}和E{X'(t)X(t+?)}

???

?a，这里????0为常

解（1）

??0

lim?

RX(?)?RX(0)

?lim?

??0

???

??????

?lim(?e?e)

??0

lim?

??0

RX(?)?RX(0)

? RX(?) 在

??0 处可导

当??0时，RX(?)?

???

e???

RX(?)??e????e???

当??0时，RX(

?)?e???e??

??e????e???,??0

?R(?)???? ??

?e?e,??0

应用随机过程应用随机过程课后习题解答毛用才胡奇英

又??0lim?R'X(?)?R'X(0)??lim???0?e????e???????????lim(??e??e)????? ???0??0?lim'RX(?)?R'X(0)??????

?RX(?)在??0处存在二阶可导数

故X(t)在??0处存在二阶可导数

由归纳可知X(t)在??0处存在n阶可导.

??e????e???,??0（2）E{X(t)X(t??)}?R(?)?????? e?e,??0?''

???e?????e???,??0 E{X(t)X(t??)}??R(?)?? ???????e??e,??0''''

11、过程{Y(t),t?(??,??)}的相关函数为RY(?)?e，对满足随机微分方程X'(t)?X(t)?Y(t)的宽平稳过程解{X(t),t?(??,??)}。[www.61k.com) ?（1）求X的均值函数，自相关函数和功率谱函数；

（2）求X与Y 的互相关函数和互功率谱函数。解: (1)令 Y(t)?ej?t，则X(t)?H(?)Y(t)，代入X'(t)?X(t)?Y(t)，有

H(?)?j?ej?t?H(?)ej?t?ej?t?H(?)?

1h(t)?2???jt?e?1 j??1??1?td??e j??1

?mX(t)?mY

???edt?2my

2?又SX(?)?H(?)SY(?)

Y是平稳过程

?SY(?)??RY?(e?)j??d??

??2 1??2

应用随机过程应用随机过程课后习题解答毛用才胡奇英

?SX(?)?

又2 2(1??)X平稳

(1??2)2] ?RX(?)?F?1[SX(?)]?F?1[

1???e?e2

?12?e,??0??2 ?? 1?e?2?,??0??2

（2）SXY(?)?H(?)Sx(?)?122 ??221?j?1??(1?j?)(1??)

???

?t?h(t)RY(??t)dt??ee

0?t?? ?RXY(?)?h(?)?RY(?)?

?dt ??

当??0时，RXY(?)? 当??0时，RXY(?)????t??t?ee0dt???1e?te?(??t)dt?(??)e?? 21??e 2

1?t?(??)et,?0??2 ?RXY(?)??

?1e??,??0??2

12、设{X(t),t?0}是均值为0的平稳的正态过程，且二阶均方可导。(www.61k.com)求证：对任意t?0，X(t)与X'(t)相互独立，但X(t)与X''(t)不相互独立，并求RXX''(t,t??)。证:（1）由定理3.6.3（P66）知，X'(t)也是正态过程由定理4.2.3知，X'(t)也是平稳过程

又E[X(t)]?0,E{X'(t)}?0 ??E{X(t)X(t)}?{E[X(s)X(t)]}s?t?R(t?s)?t?t''?R(0) t?s 39

应用随机过程应用随机过程课后习题解答毛用才胡奇英

又X(t)实平稳过程，?R(?)为偶函数

?R'(?)??R'(??)，?R'(0)??R'(0),?R'(0)?0

?E{X(t)X'(t)}?0

则X(t),X'(t)不相关，由正态变量的性质知 X(t)与X'(t)独立

（2）易知{X''(t),t?0}也是正态平稳过程

E{X''(t)}?d

dtE{X'(t)}?0

E{X(t)X''(t)}??

?tE{X(s)X'(t)}t?s?R''(0)

又D[X'(t)]??R''(0)?0

?R''(0)?0

?X(t)与X''(t)不独立

RXX''(t,t??)?E{X(t)X''(t??)}?R''(?)

13、设{X(t),t?0}是均方可导实平稳的正态过程，相关函数为R(?)，求其导数过程{X'(t),t?0}的一维、二维概率密度函数。（www.61k.com）

解: 由定理3.6.3（P'

66）知{X(t),t?0}仍为正态过程，而且

E{X'(t)}?0，E{X'(s)X'(t)}??R''(?)

的一维概率密度函数为：x2?X(t)P(x)?2R''(0)x?R ?X'(t)的二维概率密度函数为：P(x1'

1,x2)?2?Bexp{?1XB?1X2}

???R''其中X?(x(0)?R''(?)?

1,x2),B???R''(?)?R''(0)?

14.已知平稳过程的相关函数

应用随机过程应用随机过程课后习题解答毛用才胡奇英

（1）RX(?)??2e??cos?x,(??0)

（2）RX(?)??2e?(1??),(??0)

（3）RX(?)??2e?[cos?x?sin?],(??0)求谱密度。［www.61k.com]

????

解: SX(?)?

???j??2e??e?????cos??d? ?2?2?e???cos(??)?cos(??)d?

??2?e???[cos(???)??cos(???)?]d?

e???[(???)sin(???)???cos(???)]???2?(???)22??0e???[(???)sin(???)???cos(???)?]???0}22??(???) ??2?(1

?2?(???)2?1) ?2(???)2

（或

??由cos??]??2(傅氏变换可得SX(?)?F[RX(?)]?F[?2e

?????) ） ?2?(???)2?2?(???)2

（2）SX(?)?

???j??eRX(?)d? ?

???j??2e??e??(1??)d?

0??

??e

0?j???2e???(1???)d???e?j???2e??(1???)d? ??

??(21?1????) 22??j?(??j?)??j?(??j?)

4?3?2

? 222(???)

（3）SX(?)?

???e?j??RX(?)d?

应用随机过程应用随机过程课后习题解答毛用才胡奇英

???j??2?e?e??[co??s???e?

???s?i?d ]??

???e?j???e2??cos??d??

?????j??2e?????esin??]d? ?

?F[?e

2??cos??]????j??2?e????esin?]d? ?

???cos(??)esin??d??01??2???(2?2)?222??(???)?(???)?21

???2????????{(2?)?[?]}??(???)2?2?(???)2??2?(???)2?2?(???)22

15、已知平稳过程（参数连续）谱密度

（1）SX(?)????,??b

?0,其它

?b2,a???2a（2）SX(?)??(a?0)

?0,其它

?k2（3）SX(?)??22,(?k,?k为正数)

k?1???kn

求相关函数和平均功率。[www.61k.com）

1R(?)?解 X2?

?（1）RX(?)?2??????b?ej??SX(?)d?，平均功率RX(0)?12??b

?b?????SX(?)d? ?ej??ed???2?j??bj?????sinb? (ejb??e?jb?)?2?j??

?sinb??b?li? ?RX(0) ??0???

j??j??R(?)?[ed??ed?] （2）X??2???2?2???

应用随机过程应用随机过程课后习题解答毛用才胡奇英

?b2

b2(sin2???sin??) b2? ?RX(0)?lim??0??(sin2???sin??)?

n??? ??k（3）RX(?)?1

k2??k?K?1??ej??2???k??2????k2k?1ne2?k n?k2ek RX(0)?lim?? ????02?kk?1k?12?k

16、设X、Y是两平稳相关过程，且E[X （t）]?E[Y(t)]?0,RX(?)?RY(?),RXY(?)??RXY(??)，试证Z(t)?X(t)cos?0t?Y(t)sin?0t，也是平稳过程。（www.61k.com］又若X、Y的谱密度函数存在，试用X、Y的谱密度及互谱密度表出Z的谱密度。证: E{Z(t)}?E{X(t)cos?0t?Y(t)sin?0t}

?E[X(t)]cos?0t?E[Y(t)]sin?0t

E{Z(s)Z(t)}?E{[X(s)cos?0s?Y(s)sin?0s][[X(t)cos?0t?Y(t)sin?0t]}

?E{X(s)X(t)cos?0s?cos?0t?X(s)Y(t)cos?0s?sin?0t]

?E{Y(s)X(t)sin?0s?cos?0t?Y(s)Y(t)sin?0s?sin?0t] ?RX(?)?cos?0(t?s)?RXY(?)sin?0(t?s) 其中RXY(?)?RXY(?)??RXY()X,Y实过程 ?RXY(?) ?Z(t)是平稳过程

又 SX(?)?

??j??e?[RX(?)?cos?0??RXY(?)sin?0?]d?

??j??e?ej?0??e?j?0?RX(?)]d?2

?1j[SX(???0)?SX(???0)]?[SXY(???0)?SXY(???0)] 22

t?cos(?t??)，17、设X()其中??0为常数，?是特征函数为f(t)的实随机变量，

应用随机过程应用随机过程课后习题解答毛用才胡奇英

证明X为平稳过程充要条件为f(1)?f(2)。（www.61k.com]

证:

f?(t)?E{ejt?}?E{cost?}?jE{sint?} 又E{X(t)}?E{cos?}cos?t?E{sin?}sin?t

RX(t,t??)?111E{cos?cos??}?E{cos2?}?cos(2?t???)?sin(2?t???)?E{sin2?}222

?X(t)平稳?E{X(t)}?常数，R（t,t+?）与t无关? X

E{cos?}?E{sin?}?0,E{cos2?}?E{sin2?}?0?f(1)?f(2)?0

18、设X为平稳正态过程，E[X(t)]?0，R(?)是其相关函数，试证Y(t)?sgn[X(t)]是一平稳过程，且其标准相关函数为?Y(?)?

证: 易证 Y也是一平稳过程。

RY(?)?E{Y(t)Y(t??)}?P{X(t)X(t??)?0}?P{X(t)X(t??)?0}对于二维正态分布RY(?)2R(?) ?arcsinRY(0)?R(0)X，Y，若它们均值为0，相关函数r，则有结论

P{XY?0}?1?1?R(?)??，P{XY?0}??，其中sin??r，?,r?X， 2?2?2RX(0)所以 ?Y(?)???(?)?

1?2?1?2?2???2?arcsinRX(?) RX(0)

19、设{X(t),???t???}是平稳过程，S(?)为其谱密度函数。试证：对任意的h?0,Y(t)?X(t?h)?X(t)是平稳过程（即平稳过程具有平稳增量），并求Y的谱函数。

证 E{Y(t)}?E{X(t?h)?X(t)}?E{X(t?h)}?E{X(t)}?0 E{Y(t)Y(t??)}?E{[X(t?h)?X(t)][X(t???h)?X(t??)]}

?E{X(t?h)X(t???h)?X(t?h)X(t??)?X(t)X(t???h)?X(t)X(t??)}

应用随机过程应用随机过程课后习题解答毛用才胡奇英

?R(?)?R(??h)?R(??h)?R(?)

?Y(t)是平稳过程

又 SY(?)??e?j??RY(?)d?

??????

?j?? ?2e?j??R(?)d??

??????eR(??h)d???????e?j??R(??h)d?

?2SX(?)?

???e?j?uR(u)du????j?(v?h)eR(v)dv ?

?2SX(?)?e?j?hSX(?)?ej?hSX(?) ?2SX(?)(1?cos?h)

?FY(?)?

??''' 2S(?)(1?cos?h)d?X?

t,???t???}20、设{X()是均值为0，相关函数为RX(?)实正态平稳过程，证明X2(t)也是平稳过程，并求其均值及相关函数。［www.61k.com］证: 令 Y(t)?X2(t)?RX(0) 则

22E{Y(t)}?E{X(t)?R(0)}?E{X(t)}?RX(0)?0 （D{X(t)}?RX(0)） X

E{Y(t)Y(t??)}?E{[X2(t)?RX(0)][X2(t??)?RX(0)]}

?E{X2(t)X2(t??)?X2(t)RX(0)?X2(t??)RX(0)?R2

X(0)}

?E{X2(t)X2(t??)}?2E{X2(t)}RX(0)?R2

X(0)}

?E{X2(t)}E{X2(t??)}?2E2{X(t)X(t??)}?2E{X2(t)}RX(0)?R2

X(0)}

?R2

X(0)?2R2

X(?)?2R2

X(0))?R2

X(0)

?2R2

X(?)

应用随机过程应用随机过程课后习题解答毛用才胡奇英

X2(t)也是平稳过程

21.设二阶矩过程{X(t),???t???}的均值函数为E[X(t)]????t，相关函数为R(s,t)?e??t?s，其中?,?,??0都为常数。[www.61k.com]证明 Y(t)?X(t?1)?X(t)是一平稳过程，并求其均值及相关函数。

证: E{Y(t)}?E{X(t?1)?X(t)}????(t?1)?(???t)?? E{Y(t)Y(t??)}?E{[X(t?1)?X(t)][X(t???1)?X(t??)]}

?E{X(t?1)X(t???1)?X(t?1)X(t??)?X(t)X(t???1)?X(t)X(t??)}?e

??e??1?e??1?e? ?2e???e????e???1

?Y(t) 是一平稳过程

22、设{X(n),n?0,?1,?2,}是白噪声序列，试证明

Y(n)?1[X(n)?X(n?1)?m?X(n?m?1)]

是平稳时间序列，并求其相关函数及谱密度。

1m?11m?1证: E{Y(n)}?E?X(n?k)}??E{X(n?k)}?0 mk?0mk?0

1l?11i?1' E{Y(n)Y(m)}?E{[?X(n?k)][?X(m?k)]} lk?0ik?0

1i?12' ????[(n?m)?(k?k)] lik?0

?Y(n)是平稳时间序列。

??j??SY(?)??e

??01??j??i?12'RY(?)?e??[??(k?k)] ??l?i??0k?0

应用随机过程应用随机过程课后习题解答毛用才胡奇英

1i?1??j??2'?e??[??(k?k)] ??l?ik?0??0

23、设{X(t),???t???}为均方连续的平稳过程，具有谱密度S(?)，试证对每个

并用S(?)表出{X(n?),n?0,?1,?2,}的谱密??0,{X(n?),n?0,?1,?2,}是平稳序列，

度。［www.61k.com)

证: 令??t2?t1，(其中t2,t1?R,且t2?t1)

则E{X(n?)}?E{X[n(t2?t1)]}?mX

E{X(n?)X(m?)}?RX[(m?n)?]

?X(n?)平稳序列

m???SX(m?)(?)?

???e?j?m?RX(m?) e?j?m??

m??????12?????ej?m?S(?)d?

?exp{j?(?m?m)}?SX(?)d? ? ?2?m?????

?1?2?????j?m(1??)S(?)(e)d? ?X?m?0?

24.设?、?是两个相互独立的实随机变量，E??0,D??1,?的分布函数是F(x)，试证明：Z(t)??ejt?为平稳过程，且其谱函数就是F(?)。

证：E{Z(t)}?E{?ejt?}?E{?}?E{ejt?}?0

2?jt?E{Z(t)Z(t??)}?E{?e?ej(t??)?

?}?E{e}??ej?xdF(x) ???j???? Z(t)为平稳过程，且R(?)??Z??ej??dF(?)?12????ej??d[2?F(?)]

? Z(t)的谱函数为2?F(?)。

25.设{X(t),???t???}是均方可导的平稳过程，S(?)是其谱密度，试证：（1）Y(t)??e??(t?s)X(s)ds,(??0,常数) ??t

应用随机过程应用随机过程课后习题解答毛用才胡奇英

（2）Z(t)??e??(t?s)sin?(t?s)

?X(s)ds,(??0,??0均为常数)

均为平稳过程，并求它们的谱密度。(www.61k.com]

证：（1）E[Y(t)]????e??(t?s)E[X(s)]ds?

E{Y(t)Y(t??)}?E{?e??t??(t?s)tmX? X(s)ds}?t????e??(t???u)X(u)du ??t

?????t??e??(s?u??)R(u?s)duds

2t?w1?w?u?s,v?u?s?dw?e??(??w)R(w)dwdv2(t??)?w2??

1???(??w)??eRX(w)(?2w?2?)dw 2??

???e?(w??)RX(w)?(w??)dw???

?RY(?)

?Y(t)为平稳过程。 ?-?S（）=?e-j??RY(?)d? Y???e?j??[?e?(u??)RX(u)(u??)du]d???

??????????

???(u??)exp{?(u??)?j??}RX(u)dud? ?

????RX(u)e?udu?e??(??j?)(u??)d???

SY(?)?H(?)SX(?) （其中h(t)?e?ptU(t),U(t)为阶跃函数） 2

（2）E{Z(t)}?E{?e??(t?s)???tsin?(t?s)?X(s)ds} ?E{X(s)}?e??t?

????1te?s[sin?tcos?s?cos?tsin?s]ds

1?E{X(s)}?2?常数2???

R（s,t）=Z?s-?-??te??(s?t)e?u??v?1sin?(s?u)sin?(t?v)RX(v?u)dudv 220

sin?0t又Z(?)存在谱函数，可知h(t)?e??t

?0U(t),H(?)1 ?02?(a?j?)2

应用随机过程应用随机过程课后习题解答毛用才胡奇英

? SY(?)?SX(?) 222222(a??0??)?4a?

26.设Y是均方二次可导的平稳过程，X是均方连续的平稳过程，且满足：

2Y''(t)??Y'(t)??0Y(t)?X(t)，试用X的谱函数表示Y的谱函数及X与Y的互谱函

数。[www.61k.com］

jt?jt?解：（1）取X(t)?e,Y(t)?H(?)e，并代入上式得

[(j?)2??(j?)??0]H(?)?1 ?H(?)?1 2(j?)??(j?)??0

H(?)?21 22?2?2?(?2??0)

2?SY(?)?H(?)SX(?)?

??SX(?) 22222???(???0)dFX(?')' FY(?)??SY(?)d???2'2?'222???(???0)????''

（2）SXY(?)?H(?)SX(?)?

??SX(?) 2??2??j???0

?FXY(?)?

???SXY(u)du?dFX(?) 22?????j???0??

27.已知如图所示的系统，其输入X为一零均值的平稳正态过程，通过实验测得Z的功率谱密度为

SZ(?)???(?)?2? 222(???)(??1)

22试证Y也为平稳的，且RY(?)?RX(0)?2RX(?)；

利用（1）的结论分别求X和Y的自相关函数与功率谱密度。

X(t)?(?)2?h(t)?e?tU(t)?Z(t)

证（1）类似第20题

应用随机过程应用随机过程课后习题解答毛用才胡奇英

E{Y(t)}?E{X2(t)}?RX(0)

E{Y(t)Y(t??)}?E{X2(t)X2(t??)}

?E{X2(t)}E{X2(t??)}?2E2{X(t)X(t??)}

22?RX(0)?2RX(?)

（2）h(t)?e?tu(t)

????

?H(?)?

???eu(t)d?t?0?t?t1 e??jet?1?j?

SY(?)?SZ(?)

H(?)

2[??(?)??2?](?2??2)(?2?1)2(1??2)?1 ??(1??)?(?)?

?RY(?)?F?1S[Y?( )]2? ?2??2

1 ?2?

??????2j?? ?(?)(1??)?ed???e?1?????(?)d???e2????

1????e2

2 2(0) 令??0则RY(0)??1?3RX

2? ?RX(0)

2 ?RX(?)?1 21??e 2

?RX(?)? e2

SX(?)?F[RX(?)]??2(e)??? 22?2?()24?2??2

50 ?2??

应用随机过程应用随机过程课后习题解答毛用才胡奇英

抱歉，获取内容失败请稍后刷新尝试

应用随机过程应用随机过程课后习题解答毛用才胡奇英

抱歉，获取内容失败请稍后刷新尝试

应用随机过程应用随机过程课后习题解答毛用才胡奇英

抱歉，获取内容失败请稍后刷新尝试

应用随机过程应用随机过程课后习题解答毛用才胡奇英

抱歉，获取内容失败请稍后刷新尝试

应用随机过程应用随机过程课后习题解答毛用才胡奇英

抱歉，获取内容失败请稍后刷新尝试

应用随机过程应用随机过程课后习题解答毛用才胡奇英

抱歉，获取内容失败请稍后刷新尝试

应用随机过程应用随机过程课后习题解答毛用才胡奇英

抱歉，获取内容失败请稍后刷新尝试

应用随机过程应用随机过程课后习题解答毛用才胡奇英

抱歉，获取内容失败请稍后刷新尝试

本文标题：随机过程习题解答-【程阳解答】EXCELVBARandomize生成随机数的误区
本文地址： http://www.61k.com/1056216.html

61阅读

随机过程习题解答-【程阳解答】EXCELVBARandomize生成随机数的误区